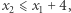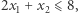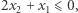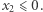Problem komiwojażera w praktyce
Korzystając z popularnych serwisów internetowych, błyskawicznie znajdziemy najkrótszą trasę między dwoma miastami. A co, gdybyśmy chcieli znaleźć najkrótszą trasę, która pozwoli po wyruszeniu z domu odwiedzić wszystkie interesujące nas miasta i wrócić do punktu wyjścia?
Możemy to pytanie sformalizować w następujący sposób. Wybrane miasta (wraz z tym, w którym mieszkamy) numerujemy od 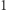 do
do 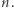 Zakładamy, że mamy tabelę
Zakładamy, że mamy tabelę 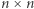 o wartościach
o wartościach 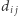 dla
dla 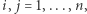 gdzie
gdzie 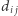 oznacza odległość (np. podaną przez nasz ulubiony serwis) z miasta
oznacza odległość (np. podaną przez nasz ulubiony serwis) z miasta 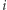 do miasta
do miasta 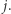 Tabela jest symetryczna, tzn.
Tabela jest symetryczna, tzn. 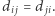 Naszym celem jest znalezienie kolejności odwiedzania miast, czyli permutacji
Naszym celem jest znalezienie kolejności odwiedzania miast, czyli permutacji 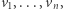 która minimalizuje długość trasy, tzn.
która minimalizuje długość trasy, tzn. 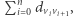 przyjmując
przyjmując 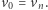 To zadanie znane jest jako problem komiwojażera i od kilkudziesięciu lat spędza sen z oczu informatykom.
To zadanie znane jest jako problem komiwojażera i od kilkudziesięciu lat spędza sen z oczu informatykom.
Z jednej strony jest to problem NP-trudny, a najlepszy w sensie złożoności pesymistycznej algorytm działa w czasie 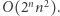 Z drugiej strony, istnieją implementacje, które dla instancji pochodzących ze świata rzeczywistego uzyskują spektakularne wyniki (tabela poniżej), ale ich pesymistyczna złożoność czasowa nie jest znana.
Z drugiej strony, istnieją implementacje, które dla instancji pochodzących ze świata rzeczywistego uzyskują spektakularne wyniki (tabela poniżej), ale ich pesymistyczna złożoność czasowa nie jest znana.
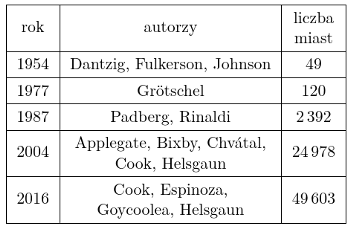
Wszystkie powyższe rekordy dotyczą optymalnych rozwiązań dla rzeczywistych map połączeń drogowych (w USA, Niemczech, Szwecji), z wyjątkiem rekordu Manfreda Padberga i Giovanniego Rinaldiego, którzy znaleźli najkrótszą trasę dla wiertarki wiercącej otwory w płytce obwodu drukowanego. Aktualnie rozwiązanie problemu na zwykłym laptopie dla 1000 miast to kwestia kilkudziesięciu sekund, ale już wynik z ostatniego wiersza tabelki (2016) uzyskano za pomocą 310 procesorów pracujących przez 8 miesięcy. Choć pierwszy wiersz tabelki wygląda skromnie, w rzeczywistości stanowi wielkie osiągnięcie, a kolejne rekordy były wynikiem rozwinięcia technik wypracowanych przez George'a Dantziga, Delberta Fulkersona i Selmera Johnsona. W dalszej części artykułu zobaczymy, jak działa ich metoda na nieco bliższym nam przykładzie 51 dużych miast w Polsce.
Kluczowy pomysł polega na zapisaniu naszego problemu jako zbioru równań i nierówności liniowych. Dla każdej pary różnych miast 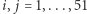 wprowadźmy zmienną
wprowadźmy zmienną 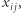 przy czym
przy czym 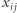 oraz
oraz 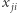 traktujemy jako dwie nazwy tej samej zmiennej. Na początek przyjmijmy, że zmienne
traktujemy jako dwie nazwy tej samej zmiennej. Na początek przyjmijmy, że zmienne 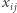 mogą przyjmować tylko dwie wartości: 0 i 1. Myślimy o nich w ten sposób, że połączenie między
mogą przyjmować tylko dwie wartości: 0 i 1. Myślimy o nich w ten sposób, że połączenie między 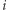 oraz
oraz 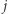 jest używane w naszym rozwiązaniu wtedy i tylko wtedy, gdy
jest używane w naszym rozwiązaniu wtedy i tylko wtedy, gdy 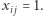 Zauważmy, że długość takiej trasy wynosi
Zauważmy, że długość takiej trasy wynosi 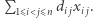
Czy możemy za pomocą prostych równań i nierówności wymusić, aby spełniające je wartości zmiennych odpowiadały dokładnie możliwym trasom komiwojażera (czyli cyklom długości 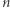 )? Pierwsza obserwacja jest prosta: dla każdego miasta
)? Pierwsza obserwacja jest prosta: dla każdego miasta 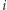 dokładnie dwie zmienne
dokładnie dwie zmienne 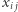 powinny mieć wartość 1, co można wyrazić jako
powinny mieć wartość 1, co można wyrazić jako 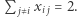 To jednak nie wystarczy, gdyż zamiast jednej trasy moglibyśmy dostać kilka krótszych, rozłącznych cykli (w skrajnym przypadku
To jednak nie wystarczy, gdyż zamiast jednej trasy moglibyśmy dostać kilka krótszych, rozłącznych cykli (w skrajnym przypadku 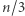 rozłącznych trójkątów).
rozłącznych trójkątów).
Aby zagwarantować, że miasta z pewnego zbioru 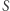 nie tworzą krótszej trasy, możemy dodać warunek eliminacji podtras, który mówi, że do tego zbioru musimy co najmniej jeden raz wejść i co najmniej jeden raz z niego wyjść. Zwykle ten warunek zapisujemy w równoważnej formie
nie tworzą krótszej trasy, możemy dodać warunek eliminacji podtras, który mówi, że do tego zbioru musimy co najmniej jeden raz wejść i co najmniej jeden raz z niego wyjść. Zwykle ten warunek zapisujemy w równoważnej formie 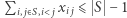 (czyli
(czyli 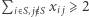 ). Równoważność łatwo dostaniemy, mnożąc oryginalną nierówność przez
). Równoważność łatwo dostaniemy, mnożąc oryginalną nierówność przez 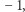 dodając do niej równości
dodając do niej równości 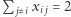 dla wszystkich
dla wszystkich 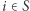 i dzieląc otrzymaną nierówność przez
i dzieląc otrzymaną nierówność przez 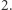 Niestety, taki warunek musimy dodać dla każdego zbioru miast
Niestety, taki warunek musimy dodać dla każdego zbioru miast 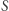 o mocy między
o mocy między 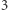 a
a 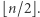 Otrzymujemy następujące zadanie, które jest przykładem tzw. programu liniowego całkowitoliczbowego.
Otrzymujemy następujące zadanie, które jest przykładem tzw. programu liniowego całkowitoliczbowego.
Zminimalizuj 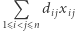 przy ograniczeniach
przy ograniczeniach
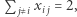 dla
dla 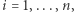
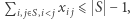 dla
dla 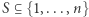 i
i 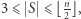
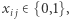 dla
dla 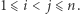
Skąd pomysł na zapisanie problemu w języku równań i nierówności liniowych? Otóż teraz rozluźniamy założenia naszego zadania: warunki 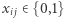 zamieniamy na
zamieniamy na 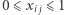 i szukamy rozwiązania w liczbach rzeczywistych. Wówczas otrzymujemy tzw. program liniowy. Tak się składa, że nasi bohaterowie umieli szybko rozwiązywać programy liniowe, gdyż jeden z nich, George Dantzig, w 1947 roku opublikował do dziś najskuteczniejszy w praktyce algorytm realizujący ten cel, nazywany algorytmem simplex. Jest on obecnie dostępny w bibliotekach dla wielu popularnych języków programowania, np. przygotowując ten artykuł, użyliśmy modułu PuLP dla języka Python.
i szukamy rozwiązania w liczbach rzeczywistych. Wówczas otrzymujemy tzw. program liniowy. Tak się składa, że nasi bohaterowie umieli szybko rozwiązywać programy liniowe, gdyż jeden z nich, George Dantzig, w 1947 roku opublikował do dziś najskuteczniejszy w praktyce algorytm realizujący ten cel, nazywany algorytmem simplex. Jest on obecnie dostępny w bibliotekach dla wielu popularnych języków programowania, np. przygotowując ten artykuł, użyliśmy modułu PuLP dla języka Python.
Plan jest następujący. Jeśli szczęśliwie jako rozwiązanie optymalne naszego programu liniowego dostaniemy same zera i jedynki, to będą one definiowały pewną trasę, która musi być optymalna, ponieważ każda trasa komiwojażera spełnia wszystkie warunki programu. Niestety może się okazać, że dostaniemy rozwiązanie ułamkowe, w którym niektóre zmienne będą miały wartość w przedziale 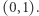 Wtedy będziemy musieli jakoś zareagować.
Wtedy będziemy musieli jakoś zareagować.
Dodatkowy kłopot polega na tym, że nasz program liniowy ma gigantyczną liczbę warunków eliminacji podtras: tylko dla 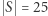 jest ich
jest ich 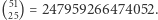 To za dużo nawet dla współczesnych komputerów. Pomysł Dantziga i jego kolegów polegał na tym, aby zacząć od prostego programu liniowego postaci:
To za dużo nawet dla współczesnych komputerów. Pomysł Dantziga i jego kolegów polegał na tym, aby zacząć od prostego programu liniowego postaci:
Zminimalizuj 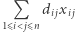 przy ograniczeniach
przy ograniczeniach
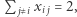 dla
dla 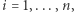
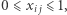 dla
dla 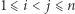 ;
;
a następnie dodawać warunki w miarę potrzeby. Taki program ma 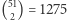 zmiennych i 2601 warunków liniowych. Uruchamiamy na komputerze algorytm simplex i w ułamku sekundy dostajemy poniższe rozwiązanie.
zmiennych i 2601 warunków liniowych. Uruchamiamy na komputerze algorytm simplex i w ułamku sekundy dostajemy poniższe rozwiązanie.
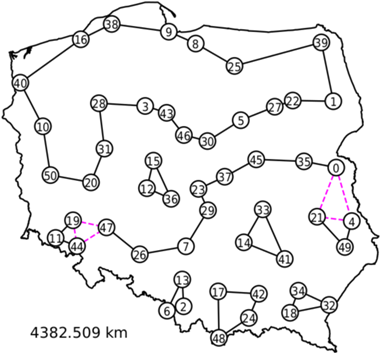
Liniami ciągłymi oznaczyliśmy zmienne o wartości 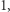 natomiast przerywanymi o wartości
natomiast przerywanymi o wartości 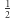 (innych ułamkowych wartości w uzyskanym rozwiązaniu nie było). Widzimy, że możemy dodać warunki eliminacji podtras dla zbiorów
(innych ułamkowych wartości w uzyskanym rozwiązaniu nie było). Widzimy, że możemy dodać warunki eliminacji podtras dla zbiorów 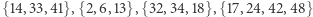 oraz
oraz 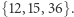 Chociaż miasta
Chociaż miasta 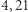 i
i 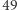 nie utworzyły krótkiego cyklu, zauważmy, że dla
nie utworzyły krótkiego cyklu, zauważmy, że dla 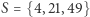 oraz dla
oraz dla 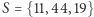 warunek eliminacji podtras też nie jest spełniony; dodajemy więc jeszcze te dwa warunki i ponownie uruchamiamy algorytm.
warunek eliminacji podtras też nie jest spełniony; dodajemy więc jeszcze te dwa warunki i ponownie uruchamiamy algorytm.
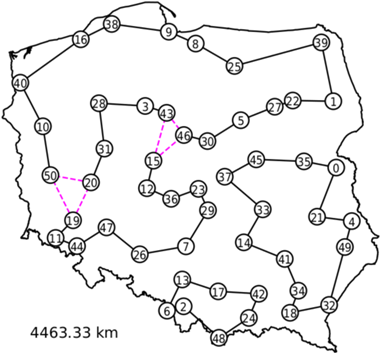
W nowym rozwiązaniu mamy nowe krótkie cykle, dodajemy warunki eliminacji podtras dla kolejnych dwóch zbiorów 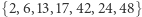 oraz
oraz 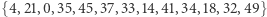 i generujemy kolejne rozwiązanie.
i generujemy kolejne rozwiązanie.
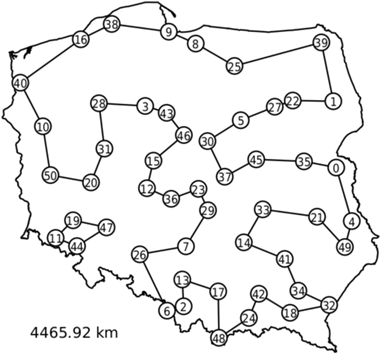
Otrzymaliśmy dwa cykle, a więc dodajemy warunek eliminacji podtras dla krótszego z nich o zbiorze wierzchołków 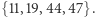 Efekt kolejnego uruchomienia algorytmu simplex widzimy poniżej.
Efekt kolejnego uruchomienia algorytmu simplex widzimy poniżej.
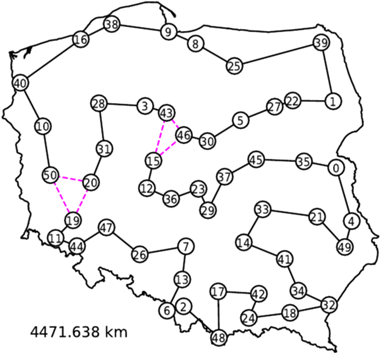
Niestety wszystkie warunki eliminacji podtras są spełnione, a jednak nie uzyskaliśmy pojedynczego cyklu. Jest to spowodowane dopuszczeniem ułamkowych wartości zmiennych. Ratunkiem w takiej sytuacji jest znalezienie nowej nierówności, którą spełniają trasy komiwojażera, ale nie spełnia jej nasze rozwiązanie. Takie nierówności nazywamy płaszczyznami odcinającymi. Dlaczego? Wyobraźmy sobie, że nasz program liniowy ma tylko dwie zmienne, a wszystkie warunki to nierówności. Wówczas zbiór punktów spełniających te warunki jest wielokątem na płaszczyźnie, jak poniżej.
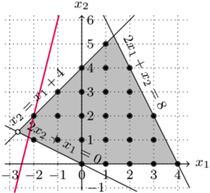
Zminimalizuj 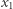 przy ograniczeniach
przy ograniczeniach
Algorytm simplex ma tę własność, że zwraca nam rozwiązanie optymalne, które jest wierzchołkiem wielokąta. Tymczasem my szukamy całkowitoliczbowego rozwiązania optymalnego. Możemy wówczas do programu liniowego dodać nierówność, która oddzieli nasz wierzchołek od wszystkich punktów o współrzędnych całkowitych wewnątrz wielokąta, odcinając fragment wielokąta za pomocą linii prostej (na rysunku fioletowa linia jest przykładem takiej prostej). W wyniku tej procedury możemy znów dostać rozwiązanie niecałkowitoliczbowe, wówczas powtarzamy operację. Z analogiczną sytuacją mamy do czynienia w większej liczbie wymiarów, gdzie uogólnieniem linii jest hiperpłaszczyzna.
Wróćmy do ostatniego rozwiązania i spójrzmy na trójkąt 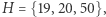 którego krawędzie odpowiadają zmiennym połówkowym
którego krawędzie odpowiadają zmiennym połówkowym 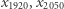 i
i 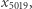 oraz na sąsiadujące z nim połączenia
oraz na sąsiadujące z nim połączenia 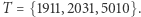 W naszym rozwiązaniu suma
W naszym rozwiązaniu suma 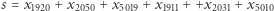 wynosi
wynosi 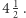 Tymczasem w dowolnej trasie komiwojażera
Tymczasem w dowolnej trasie komiwojażera 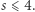 Dlaczego? Z warunku
Dlaczego? Z warunku 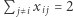 dla
dla 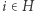 wiemy, że
wiemy, że

Dodając stronami te nierówności i trywialną 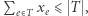 otrzymujemy
otrzymujemy 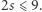 Ale jeśli zmienne opisują trasę komiwojażera, to
Ale jeśli zmienne opisują trasę komiwojażera, to  jest liczbą całkowitą, a wtedy otrzymana nierówność jest równoważna
jest liczbą całkowitą, a wtedy otrzymana nierówność jest równoważna 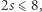 czyli
czyli 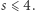 Zachęcamy w tym miejscu Pracowitego Czytelnika, aby wykazał, że ogólniej, dla dowolnego zbioru miast
Zachęcamy w tym miejscu Pracowitego Czytelnika, aby wykazał, że ogólniej, dla dowolnego zbioru miast 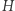 i nieparzystej liczby połączeń
i nieparzystej liczby połączeń 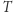 wychodzących z
wychodzących z 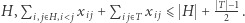 Są to tzw. nierówności 2-skojarzeniowe, gdyż zostały odkryte w kontekście problemu skojarzeń w grafach. Do naszego programu dodajmy nierówność 2-skojarzeniową
Są to tzw. nierówności 2-skojarzeniowe, gdyż zostały odkryte w kontekście problemu skojarzeń w grafach. Do naszego programu dodajmy nierówność 2-skojarzeniową 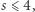 która pozwoli się pozbyć połówkowego trójkąta
która pozwoli się pozbyć połówkowego trójkąta 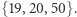 Okazuje się, że w rozwiązaniu optymalnym takiego programu liniowego wszystkie zmienne mają już wartość 0 lub 1, a odpowiadające im rozwiązanie tworzy pojedynczy cykl, a więc jest optymalną trasą komiwojażera. Wygląda ona następująco.
Okazuje się, że w rozwiązaniu optymalnym takiego programu liniowego wszystkie zmienne mają już wartość 0 lub 1, a odpowiadające im rozwiązanie tworzy pojedynczy cykl, a więc jest optymalną trasą komiwojażera. Wygląda ona następująco.
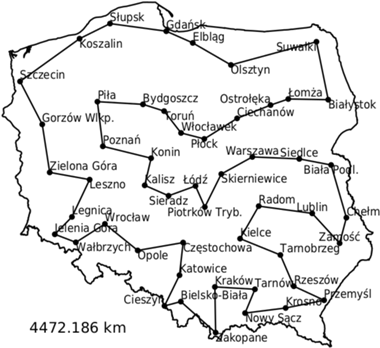
Dantzig z kolegami nie odkryli nierówności 2-skojarzeniowych, podobnie jak w naszym przykładzie nierówności eliminacji podtras nie były wystarczające, więc musieli użyć dwóch dziwacznych nierówności. W kolejnych latach odkryto metody automatycznego znajdowania płaszczyzn odcinających, jednak wciąż najbardziej skuteczne okazują się rodziny płaszczyzn (czyli po prostu nierówności) projektowane z myślą o konkretnym problemie, jak nasze nierówności 2-skojarzeniowe. Dla problemu komiwojażera odkryto wiele takich rodzin. Dla niektórych z nich jesteśmy w stanie szybko (w czasie wielomianowym) znajdować nierówność niespełnioną przez dane rozwiązanie, o ile taka istnieje (jest to możliwe dla nierówności eliminacji podtras i nierówności 2-skojarzeniowych). Dla innych stosujemy heurystyki, które wprawdzie działają szybko, ale mogą pozostawić jakąś niespełnioną nierówność.
Dociekliwy Czytelnik na pewno zadaje sobie teraz pytanie, co się dzieje, gdy program rozwiązujący problem komiwojażera nie miał tyle szczęścia co my z mapą Polski i w pewnym kroku generuje rozwiązanie, które nie jest całkowitoliczbowe, a mimo to wszystkie rodziny nierówności, które jest w stanie sprawdzić, są spełnione. Odpowiedź jest prosta: wówczas używa się brutalnej siły. Wybieramy dowolną zmienną 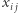 o wartości w przedziale
o wartości w przedziale 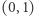 i rekurencyjnie rozwiązujemy dwa podproblemy. W pierwszym dodajemy warunek
i rekurencyjnie rozwiązujemy dwa podproblemy. W pierwszym dodajemy warunek 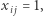 w drugim
w drugim 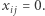 Zauważmy, że każda optymalna trasa komiwojażera spełnia warunki dokładnie jednego z tych podproblemów. W każdym z podproblemów możemy znowu szukać płaszczyzn odcinających i rozgałęziać się na kolejne podproblemy. W ten sposób znajdziemy wiele tras komiwojażera, z których najkrótsza będzie optymalna.
Zauważmy, że każda optymalna trasa komiwojażera spełnia warunki dokładnie jednego z tych podproblemów. W każdym z podproblemów możemy znowu szukać płaszczyzn odcinających i rozgałęziać się na kolejne podproblemy. W ten sposób znajdziemy wiele tras komiwojażera, z których najkrótsza będzie optymalna.
Liczba podproblemów może szybko wymknąć się spod kontroli, bo 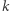 poziomów rozgałęzień to
poziomów rozgałęzień to 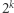 podproblemów. Z pomocą przychodzą wówczas heurystyki znajdujące niekoniecznie optymalne trasy komiwojażera (obecnie najskuteczniejsza, heurystyka Lina-Kernighana-Helsgauna, dla mapy świata zawierającej
podproblemów. Z pomocą przychodzą wówczas heurystyki znajdujące niekoniecznie optymalne trasy komiwojażera (obecnie najskuteczniejsza, heurystyka Lina-Kernighana-Helsgauna, dla mapy świata zawierającej 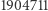 miast znajduje trasę dłuższą od optymalnej o co najwyżej 0,023 %). Powiedzmy, że heurystyka znalazła nam trasę komiwojażera o długości
miast znajduje trasę dłuższą od optymalnej o co najwyżej 0,023 %). Powiedzmy, że heurystyka znalazła nam trasę komiwojażera o długości 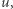 i rozważmy podproblem, w którym wartość rozwiązania optymalnego programu liniowego wynosi
i rozważmy podproblem, w którym wartość rozwiązania optymalnego programu liniowego wynosi 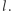 Każda trasa, którą możemy znaleźć w tym podproblemie, będzie miała długość co najmniej
Każda trasa, którą możemy znaleźć w tym podproblemie, będzie miała długość co najmniej 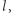 a więc jeśli
a więc jeśli 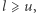 to taki podproblem możemy zignorować, gdyż nie pozwoli on znaleźć lepszej trasy niż ta, którą już mamy. Dzięki temu możliwe jest znaczne ograniczenie szybkiego wzrostu liczby podproblemów.
to taki podproblem możemy zignorować, gdyż nie pozwoli on znaleźć lepszej trasy niż ta, którą już mamy. Dzięki temu możliwe jest znaczne ograniczenie szybkiego wzrostu liczby podproblemów.
Okazuje się, że dla danych pochodzących ze świata rzeczywistego i dostatecznie bogatych rodzin płaszczyzn oddzielających liczba generowanych podproblemów nie jest astronomiczna. Jest to jednak jedynie obserwacja empiryczna. W 2018 roku Stefan Hougardy i Xianghui Zhong wymyślili sposób generowania sztucznych, wyjątkowo trudnych instancji problemu komiwojażera. Na podstawie testów oszacowali, że Concorde, najlepszy obecnie program korzystający z naszkicowanej w tym artykule metody, uruchomiony na współczesnym komputerze potrzebuje 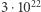 lat obliczeń dla wygenerowanej przez nich instancji 1000 miast. To pokazuje, że przynajmniej na razie NP-trudności problemu nie dało się oszukać. Na szczęście duże instancje problemu komiwojażera rozwiązane optymalnie lub niemal optymalnie pokazują, że świat wokół nas rzadko jest aż tak złośliwy jak generator Hougardy'ego i Zhonga.
lat obliczeń dla wygenerowanej przez nich instancji 1000 miast. To pokazuje, że przynajmniej na razie NP-trudności problemu nie dało się oszukać. Na szczęście duże instancje problemu komiwojażera rozwiązane optymalnie lub niemal optymalnie pokazują, że świat wokół nas rzadko jest aż tak złośliwy jak generator Hougardy'ego i Zhonga.
Optymalna trasa dla 51 polskich miast zaprezentowana w tym artykule została obliczona na podstawie tabeli 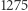 długości najkrótszych połączeń drogowych między nimi, znalezionych za pomocą serwisu Google maps we wrześniu 2019 roku. Dane oraz prosty skrypt w języku Python, który znajduje optymalną trasę i tworzy rysunki do tego artykułu, są dostępne na github.com/lkowalik/tsp. Zachęcamy do eksperymentów!
długości najkrótszych połączeń drogowych między nimi, znalezionych za pomocą serwisu Google maps we wrześniu 2019 roku. Dane oraz prosty skrypt w języku Python, który znajduje optymalną trasę i tworzy rysunki do tego artykułu, są dostępne na github.com/lkowalik/tsp. Zachęcamy do eksperymentów!