Złożoność algorytmów teorioliczbowych

Rozważmy następujący algorytm:

Jak łatwo sprawdzić, podany kod zwraca najmniejszy nietrywialny czynnik podanej na wejściu liczby 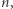$|n,$ bądź 0 - gdy takiego czynnika nie ma (bo np. 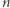$|n$ jest liczbą pierwszą).

Zastanówmy się, jaka jest złożoność podanego programu. Pętla while wykona co najwyżej 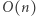$|O(n)$ obrotów. W pojedynczym jej wykonaniu niemal wszystkie operacje mają koszt stały, poza operacją while której koszt możemy bardzo zgrubnie oszacować z góry przez 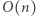$O(n) |$ (w rzeczywistości można łatwo osiągnąć 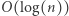$|O(log(n))$ ). Oznacza to, że cały algorytm działa w czasie nie większym niż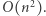 $|O(n2).$

Czy oznacza to, że właśnie pokazaliśmy wielomianowy algorytm na szukanie nietrywialnych czynników? Rozkład nawet dużych liczb na czynniki pierwsze już nie jest dla nas kłopotem?

Oczywiście, nic z tych rzeczy.

Nieporozumienie bierze się z problemu z ustaleniem, co jest parametrem, względem którego liczymy złożoność programów komputerowych. Otóż parametrem jest dla nas zawsze rozmiar danych, ale rozumiany jako długość napisu reprezentującego wejście. Konkretniej: 1000000000 ma dla nas rozmiar "dziesięć", a nie "miliard"...

Wracając do naszego algorytmu: jeśli rozmiar danych to 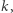$k, |$ to wówczas liczba 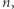$|n,$ którą reprezentują te dane jest rzędu 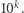$k |10 .$ Skoro więc oszacowaliśmy czas działania algorytmu przez 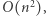$O(n2),$ to w języku rozmiaru danych przekłada się to na 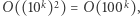$O((10k)2)$ czyli jest jednak wykładniczy od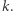 $|k.$

Potencjalny algorytm wielomianowy na rozkład na czynniki musiałby więc być pewnie nieco bardziej wyrafinowany...