Informatyczny kącik olimpijski

Beautiful Password

Tym razem omówimy zadanie "Beautiful Password", które pojawiło się na konkursie Cuprum 2018 organizowanym przez firmę Codility.

Zadanie. Dane jest słowo 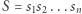$|S = s s ...s 1 2 n$ o długości 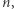$n,$ zawierające małe litery alfabetu angielskiego. Ustal długość najdłuższego podsłowa, zawierającego wyłącznie wystąpienia dwóch różnych liter w tych samych krotnościach. Przykładowo dla 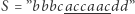$|S =”bbbcaccaacdd ”$ odpowiedzią jest 6.

Rozwiązanie 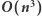$|O$
Pierwsze rozwiązanie, które przychodzi do głowy, polega na niezależnym sprawdzeniu każdego z 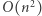$O(n2)$ podsłów - czy ma ono dokładnie dwie różne litery występujące w tych samych krotnościach. Aby to zrobić, wystarczy przejść po sprawdzanym podsłowie i zliczyć wystąpienia każdej litery. Czas potrzebny na sprawdzenie jednego podsłowa jest proporcjonalny do jego długości. Zatem całe rozwiązanie działa w czasie 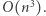$O(n3). |$ Alfabet ma stały rozmiar (26 liter), więc został pominięty w obliczeniu złożoności czasowej.

Rozwiązanie 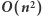$|O$
Szybsze rozwiązanie polega na tym, aby każdą literę słowa 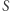$|S$ rozważyć jako pierwszą literę poszukiwanego podsłowa. Mając ustaloną pozycję początkową, przeglądamy kolejne litery, zliczając liczbę wystąpień każdej litery od a do z. Jeśli w którymś momencie dokładnie dwie litery będą miały taką samą dodatnią liczbę wystąpień oraz żadna inna litera się nie pojawiła, to znaleźliśmy podsłowo o poszukiwanych własnościach. Spośród znalezionych słów wybieramy najdłuższe i jego długość wypisujemy. Pozycji początkowych jest 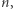$n,$ dla każdej z nich przeglądamy wszystkie litery na prawo, co daje złożoność czasową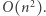 $O(n$

Warunek: dokładnie dwie litery
W procesie rozwiązywania zadania dobrze jest pomyśleć o różnych wariantach zadania macierzystego. W tym zadaniu możemy osłabić jeden z warunków. Otóż znajdźmy najdłuższe podsłowo, które ma dokładnie dwie różne litery (pomijamy warunek o tej samej krotności wystąpień). Takie zadanie można rozwiązać za pomocą metody gąsienicy. Na początku ustawiamy prawy i lewy koniec gąsienicy na pierwszej literze. Następnie rozszerzamy gąsienicę w prawo, dopóki pokrywa ona wystąpienia co najwyżej dwóch różnych liter. W przeciwnym przypadku skracamy gąsienicę, przesuwając lewy koniec w prawo. Pozostało nam jeszcze opisać, w jaki sposób zapisywać w pamięci liczbę różnych liter, które pokrywa gąsienica. W tym celu dla każdej litery od a do z zapamiętajmy, ile razy ta litera występuje. Gdy przesuwamy prawy koniec gąsienicy, to zwiększamy liczbę wystąpień litery, którą właśnie dodaliśmy do gąsienicy. Kiedy zaś skracamy gąsienicę, to zmniejszamy liczbę wystąpień litery, która została usunięta z gąsienicy.

Prawy i lewy koniec gąsienicy wykonają po 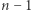$n − 1$ ruchów. Aktualizacji przechowywanych wartości dokonujemy w czasie stałym. Zatem otrzymaliśmy rozwiązanie, które działa w czasie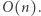 $O(n).$

Warunek: ta sama liczba wystąpień
Weźmy na warsztat wersję zadania, w którym założymy, że 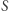$S |$ zawiera wystąpienia co najwyżej dwóch różnych liter. Bez straty ogólności możemy założyć, że te litery to a i b. Chcemy znaleźć najdłuższe podsłowo, które ma tyle samo wystąpień a co b. W tym celu literze a przypiszmy wartość 1, zaś b wartość -1. Intuicyjnie chcemy, żeby suma wartości dwóch różnych liter sumowała się do 0. Niech zatem 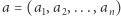$|a = (a1,a2,...,an)$ oznacza wartości przypisane kolejnym literom.

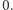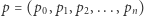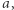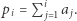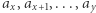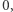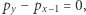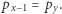Wówczas szukamy najdłuższego fragmentu w $|a$ o sumie $|0.$ Niech teraz $|p = (p0,p1,p2,...,pn)$ oznacza sumy prefiksowe $a,$ gdzie $|p = Pi a . i j 1 j$ Podsłowo $a ,a ,...,a x x+1 y$ ma sumę $0,$ jeśli $|p − p = 0, y x− 1$ czyli $|px−1 = py.$ Zatem w ciągu sum prefiksowych szukamy dwóch takich samych wartości, pomiędzy którymi odległość jest najmniejsza. Aby to zrobić, wystarczy dla każdej wartości znaleźć jej pierwsze i ostatnie wystąpienie (można to zrobić za pomocą metody zliczania) i wziąć różnicę tych indeksów. Spośród wyników dla poszczególnych wartości wybieramy ten największy.

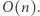Wartości, które pojawią się w ciągu sum prefiksowych, są z przedziału $|[− n;n],$ zatem jest ich $O(n).$ Wszystkie pozostałe kroki rozwiązania również wykonują 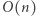$O(n)$ operacji, a więc całe rozwiązanie działa w czasie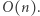 $|O(n).$

Rozwiązanie 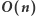$O |$
Wróćmy do oryginalnej wersji zadania. Powyższe rozważania zastosujemy w rozwiązaniu wzorcowym. Otóż podzielmy słowo na bloki złożone z tych samych liter. Np. 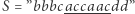$S =”bbbcaccaac dd” -------$ ma następujący podział 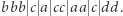$|bbb c a cc aa c dd.$ Następnie zastosujmy metodę gąsienicy (podobnie jak w podzadaniu "Warunek: dokładnie dwie litery") na wyznaczonych blokach. Przesuwamy prawy koniec gąsienicy dopóki występują co najwyżej dwie różne litery. W przeciwnym przypadku przesuwamy lewy koniec aż do uzyskania wystąpień dokładnie jednej litery. Na rysunku zostały przedstawione fragmenty słowa pokrywane przez gąsienicę po kolejnych fazach rozszerzania, a przed skracaniem:

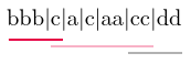
Na otrzymanych fragmentach uruchamiamy algorytm opisany w sekcji "Warunek: ta sama liczba wystąpień". Zauważmy, że każdy blok liter należy do co najwyżej dwóch takich fragmentów. Stąd złożoność czasowa rozwiązania wynosi $O(n).$