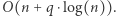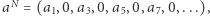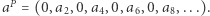Informatyczny kącik olimpijski
XORanges
W tym odcinku omówimy rozwiązanie zadania XORanges, które pojawiło się na trzecich zawodach European Junior Olympiad in Informatics (Maribor, Słowenia).
Zadanie (XORanges). Dany jest ciąg 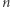 liczb naturalnych
liczb naturalnych 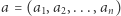 oraz
oraz 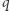 poleceń dwóch typów. 1) Zmień wartość
poleceń dwóch typów. 1) Zmień wartość 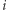 -tego elementu. 2) Podaj współczynnik przedziału
-tego elementu. 2) Podaj współczynnik przedziału 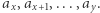 Współczynnik przedziału
Współczynnik przedziału 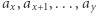 obliczamy w następujący sposób: dla każdego podsłowa (spójnego fragmentu) tego przedziału liczymy xor jego wartości, następnie xorujemy te wyniki, otrzymując współczynnik przedziału. Przykładowo współczynnik przedziału
obliczamy w następujący sposób: dla każdego podsłowa (spójnego fragmentu) tego przedziału liczymy xor jego wartości, następnie xorujemy te wyniki, otrzymując współczynnik przedziału. Przykładowo współczynnik przedziału 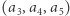 wynosi
wynosi 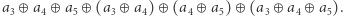 Zaproponuj algorytm, który jest w stanie możliwie szybko wykonać wszystkie polecenia podane na wejściu.
Zaproponuj algorytm, który jest w stanie możliwie szybko wykonać wszystkie polecenia podane na wejściu.
Na początku przyjmijmy, że polecenia typu 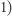 będziemy wykonywali w czasie
będziemy wykonywali w czasie 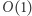 poprzez zmianę wartości
poprzez zmianę wartości 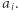 Zatem zajmijmy się odpowiedziami na polecenia typu
Zatem zajmijmy się odpowiedziami na polecenia typu 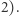 Załóżmy, że chcemy obliczyć współczynnik
Załóżmy, że chcemy obliczyć współczynnik 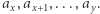 Na potrzeby artykułu wprowadźmy kilka oznaczeń. Niech:
Na potrzeby artykułu wprowadźmy kilka oznaczeń. Niech:
![[ai;a j]](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/7x-61a8b259034078a8200edbad113df6a242cbf680-im-33,33,33-FF,FF,FF.gif) oznacza ciąg
oznacza ciąg 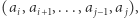
- "xor podsłowa
![[ai;a j]](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/10x-61a8b259034078a8200edbad113df6a242cbf680-im-33,33,33-FF,FF,FF.gif) " oznacza wartość
" oznacza wartość 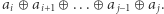
Rozwiązanie 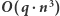
Pierwsze rozwiązanie polega na obliczeniu xora każdego z 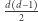 podsłów, gdzie
podsłów, gdzie 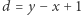 i oznacza długość przedziału
i oznacza długość przedziału ![[x;y].](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/4x-976e93dcbfe4c97ee97795bf70ba40f010ea99f3-im-33,33,33-FF,FF,FF.gif) Obliczenie xora podsłowa odbywa się za pomocą metody naiwnej, polegającej na przejściu po wszystkich elementach. Na koniec xorujemy powyższe wyniki. Rozwiązanie dla jednego polecenia działa w czasie
Obliczenie xora podsłowa odbywa się za pomocą metody naiwnej, polegającej na przejściu po wszystkich elementach. Na koniec xorujemy powyższe wyniki. Rozwiązanie dla jednego polecenia działa w czasie 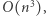 zatem całkowita złożoność to
zatem całkowita złożoność to 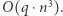
Rozwiązanie 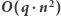
W tym rozwiązaniu, podobnie jak wyżej, obliczymy xor podsłów ![|[a ;a ] x y](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/2x-8819d5fbd6a4b4855eca7411b39ccace18220e80-im-33,33,33-FF,FF,FF.gif) (dla wszystkich
(dla wszystkich 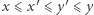 ) niezależnie. Jednak tym razem, zamiast naiwnej metody, skorzystamy z obserwacji, że:
) niezależnie. Jednak tym razem, zamiast naiwnej metody, skorzystamy z obserwacji, że:

gdzie 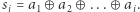 Ciąg
Ciąg 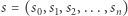 ma analogiczną konstrukcję do ciągu sum prefiksowych i możemy go wygenerować w czasie
ma analogiczną konstrukcję do ciągu sum prefiksowych i możemy go wygenerować w czasie 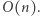 Otóż
Otóż 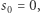 zaś
zaś 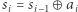 (dla
(dla 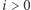 ). W ten sposób otrzymaliśmy rozwiązanie działające w czasie
). W ten sposób otrzymaliśmy rozwiązanie działające w czasie 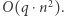
Rozwiązanie 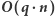
Przypomnijmy proste fakty:
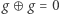 (dla
(dla 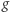 naturalnego),
naturalnego),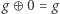 (dla
(dla 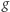 naturalnego),
naturalnego),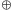 jest operacją łączną i przemienną.
jest operacją łączną i przemienną.
Na podstawie powyższych faktów możemy zauważyć, że do obliczenia współczynnika przedziału wystarczy znać parzystość liczby wystąpień każdego elementu w wyrażeniu je opisującym. Przykładowo:

gdyż 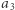 i
i 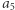 występują nieparzyście wiele razy w całym wyrażeniu, zaś
występują nieparzyście wiele razy w całym wyrażeniu, zaś 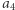 występuje parzyście wiele razy.
występuje parzyście wiele razy.
Zastanówmy się, ile razy 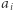 (dla
(dla 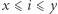 ) występuje we wzorze opisującym współczynnik przedziału
) występuje we wzorze opisującym współczynnik przedziału ![|[ax;ay].](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/3x-23b9068cbe0c349734bd2fbff54b60656fdb4d3c-im-33,33,33-FF,FF,FF.gif) Innymi słowy chcemy obliczyć, w ilu podsłowach występuje
Innymi słowy chcemy obliczyć, w ilu podsłowach występuje 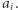 Niech
Niech 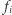 oznacza tę wartość. Otóż początkiem takiego podsłowa może być element o numerze z przedziału
oznacza tę wartość. Otóż początkiem takiego podsłowa może być element o numerze z przedziału ![|[x; i],](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/6x-23b9068cbe0c349734bd2fbff54b60656fdb4d3c-im-33,33,33-FF,FF,FF.gif) końcem zaś element o numerze z przedziału
końcem zaś element o numerze z przedziału ![[i;y].](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/7x-23b9068cbe0c349734bd2fbff54b60656fdb4d3c-im-33,33,33-FF,FF,FF.gif)

Zatem 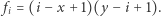 Współczynnik przedziału to xor zbioru
Współczynnik przedziału to xor zbioru 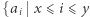 i
i 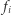 jest nieparzyste
jest nieparzyste 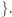 Wyznaczenie tego zbioru realizujemy w czasie
Wyznaczenie tego zbioru realizujemy w czasie 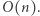 Zatem całe rozwiązanie działa w czasie
Zatem całe rozwiązanie działa w czasie 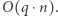
Rozwiązanie 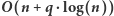
Przed nami rozwiązanie wzorcowe. Polecenie 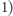 będziemy wykonywali nieco inaczej niż poprzednio, ale najpierw opiszemy operację
będziemy wykonywali nieco inaczej niż poprzednio, ale najpierw opiszemy operację 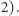
Przeanalizujmy parzystości elementów ciągu 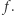 Otóż
Otóż 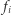 jest nieparzyste, jeśli
jest nieparzyste, jeśli 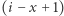 i
i 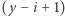 są nieparzyste. Stąd
są nieparzyste. Stąd 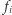 jest nieparzyste wtedy i tylko wtedy, gdy
jest nieparzyste wtedy i tylko wtedy, gdy 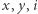 są tej samej parzystości. Zatem jeśli
są tej samej parzystości. Zatem jeśli  i
i 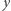 są różnej parzystości, to odpowiedzią jest
są różnej parzystości, to odpowiedzią jest 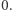 W przeciwnym przypadku odpowiedzią jest:
W przeciwnym przypadku odpowiedzią jest:

Chcemy szybko znajdować wartość powyższego wyrażenia. Zauważmy, że jest to xor elementów na pozycjach parzystych lub nieparzystych ciągu ![|[ax;ay].](/math/temat/informatyka/algorytmy/2019/10/30/XORanges/11x-1d4a5fca1303064c4a5a7dc8b6c2ee4eb8f8023a-im-33,33,33-FF,FF,FF.gif) Niech zatem:
Niech zatem:
Wówczas dla 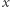 parzystego odpowiedzią jest
parzystego odpowiedzią jest 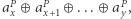 zaś dla
zaś dla 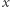 nieparzystego odpowiedzią jest
nieparzystego odpowiedzią jest 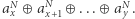
Zbudujmy dwa drzewa przedziałowe. Liśćmi pierwszego z nich niech będą wartości ciągu 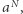 zaś liśćmi drugiego niech będą wartości ciągu
zaś liśćmi drugiego niech będą wartości ciągu 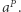 Pozostałe węzły będą przechowywały xor wartości dzieci. Taka struktura pozwala w czasie
Pozostałe węzły będą przechowywały xor wartości dzieci. Taka struktura pozwala w czasie 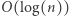 znajdować
znajdować 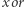 przedziału oraz w tym samym czasie obsługiwać operację zmiany wartości elementu (polecenie typu pierwszego). Zatem całe rozwiązanie działa w czasie
przedziału oraz w tym samym czasie obsługiwać operację zmiany wartości elementu (polecenie typu pierwszego). Zatem całe rozwiązanie działa w czasie