Historia pewnego trenera
Czy pokazując poprawność algorytmu, warto sięgnąć po matematyczne twierdzenia? Jak najbardziej! Przekonamy się o tym, rozważając problem zbalansowanego rozwoju w 2-wymiarowych systemach dodawania wektorów ( Vector Addition Systems - VAS), ubrany w historyjkę o zawodniku i trenerze.
Rozważmy trenera, który trenuje jednego zawodnika. Co pewien czas, na przykład co 3 miesiące, trener musi wybrać metodę treningową na kolejny okres z pewnej skończonej puli metod  W tym celu korzysta z pomocy symulatora, w którym może sprawdzić, jakie umiejętności będzie miał dany zawodnik po zastosowaniu metody
W tym celu korzysta z pomocy symulatora, w którym może sprawdzić, jakie umiejętności będzie miał dany zawodnik po zastosowaniu metody 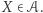 Zależy mu na znalezieniu takiego ciągu metod, aby po ich kolejnym zastosowaniu zawodnik rozwinął się w sposób zbalansowany - o tym, co przez to rozumiemy, za chwilę.
Zależy mu na znalezieniu takiego ciągu metod, aby po ich kolejnym zastosowaniu zawodnik rozwinął się w sposób zbalansowany - o tym, co przez to rozumiemy, za chwilę.
Zakładamy, że zawodnik 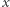 jest w całości opisany przez parę liczb naturalnych, na przykład: szybkość, technika. Założymy również, że metody trenera to wektory liczb całkowitych, a aplikacja metody do zawodnika powoduje przesunięcie jego umiejętności o taki właśnie wektor, o ile nie powoduje to "zejścia" któregoś z parametrów poniżej zera.
jest w całości opisany przez parę liczb naturalnych, na przykład: szybkość, technika. Założymy również, że metody trenera to wektory liczb całkowitych, a aplikacja metody do zawodnika powoduje przesunięcie jego umiejętności o taki właśnie wektor, o ile nie powoduje to "zejścia" któregoś z parametrów poniżej zera.
Mówimy, że zawodnik 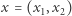 jest z całą pewnością lepszy lub równy zawodnikowi
jest z całą pewnością lepszy lub równy zawodnikowi 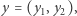 co zapisujemy
co zapisujemy 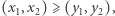 jeżeli jest co najmniej tak samo szybki i wyszkolony technicznie, czyli gdy jednocześnie
jeżeli jest co najmniej tak samo szybki i wyszkolony technicznie, czyli gdy jednocześnie 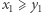 i
i 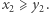 Jeżeli dodatkowo nie jest mu równy, czyli
Jeżeli dodatkowo nie jest mu równy, czyli 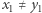 lub
lub 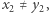 to piszemy
to piszemy 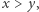 na przykład
na przykład 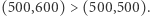 Uważny Czytelnik od razu spostrzeże, że niektórzy zawodnicy są nieporównywalni, na przykład
Uważny Czytelnik od razu spostrzeże, że niektórzy zawodnicy są nieporównywalni, na przykład 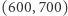 i
i 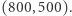 Powiemy, że zawodnik rozwinął się (w sposób zbalansowany), jeżeli stał się z całą pewnością lepszy. Ścieżką treningową nazywamy dowolny ciąg metod treningowych
Powiemy, że zawodnik rozwinął się (w sposób zbalansowany), jeżeli stał się z całą pewnością lepszy. Ścieżką treningową nazywamy dowolny ciąg metod treningowych 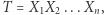 a efekt zastosowania kolejno metod
a efekt zastosowania kolejno metod 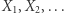 dla zawodnika
dla zawodnika 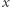 będziemy oznaczać przez
będziemy oznaczać przez 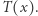 Ścieżkę
Ścieżkę 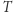 nazwiemy rozwojową dla zawodnika
nazwiemy rozwojową dla zawodnika 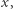 jeżeli po jej zastosowaniu rozwinął się, czyli gdy
jeżeli po jej zastosowaniu rozwinął się, czyli gdy 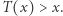
Przykład 1. Niech 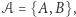 gdzie
gdzie 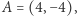 a
a 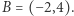 Ścieżka
Ścieżka 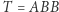 jest rozwojowa dla
jest rozwojowa dla 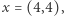 gdyż
gdyż 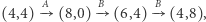 a
a 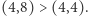 Nie jest ona rozwojowa dla
Nie jest ona rozwojowa dla 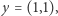 ponieważ w tym punkcie nie można zastosować metody
ponieważ w tym punkcie nie można zastosować metody 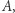 gdyż
gdyż 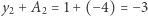 jest liczbą ujemną. Co więcej, dla
jest liczbą ujemną. Co więcej, dla 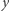 nie ma żadnej ścieżki rozwojowej.
nie ma żadnej ścieżki rozwojowej.
Sformułujemy teraz problem w sposób ścisły i zaproponujemy algorytm, który ma go rozwiązywać.
Problem (zbalansowanego rozwoju).
Dane wejściowe:
punkt (startowy) 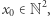
skończony zbiór 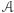 par liczb całkowitych (wektorów).
par liczb całkowitych (wektorów).
Pytanie: czy istnieje taki ciąg punktów kratowych w ćwiartce dodatniej 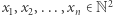 , że dla każdego
, że dla każdego 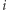 istnieje wektor
istnieje wektor 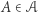 taki, że
taki, że 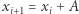 oraz
oraz 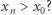
Najpierw podamy bez dowodu pewien lemat pomocniczy.
Lemat 1. Istnieje ścieżka rozwojowa z 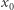 wtedy i tylko wtedy, gdy istnieje ścieżka rozwojowa z pewnego punktu
wtedy i tylko wtedy, gdy istnieje ścieżka rozwojowa z pewnego punktu 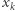 osiągalnego z
osiągalnego z 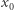 (czyli takiego, że
(czyli takiego, że 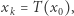 dla pewnej ścieżki
dla pewnej ścieżki 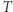 ).
).
Mając na uwadze powyższy lemat, będziemy zajmować się pytaniem, czy jest punkt 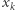 osiągalny z
osiągalny z 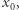 z którego istnieje ścieżka rozwojowa. Równoważnie: szukamy ścieżki
z którego istnieje ścieżka rozwojowa. Równoważnie: szukamy ścieżki 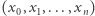 takiej, że
takiej, że 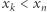 dla jakiegoś
dla jakiegoś 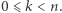
Algorytm. Konstruujemy kandydata na 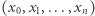 przez back-tracking, czyli "jak nie wyjdzie, to zrób krok wstecz i pójdź w innym kierunku": będąc w punkcie
przez back-tracking, czyli "jak nie wyjdzie, to zrób krok wstecz i pójdź w innym kierunku": będąc w punkcie 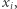 aplikujemy niezaaplikowaną do tej pory w tym punkcie metodę
aplikujemy niezaaplikowaną do tej pory w tym punkcie metodę 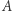 (o ile jest taka), otrzymując kolejny punkt na ścieżce
(o ile jest taka), otrzymując kolejny punkt na ścieżce 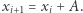 Gdy "nie wyjdzie", czyli gdy
Gdy "nie wyjdzie", czyli gdy 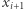 jest mniejszy lub równy pewnemu
jest mniejszy lub równy pewnemu 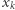 obecnemu już na ścieżce, robimy "krok wstecz", czyli usuwamy
obecnemu już na ścieżce, robimy "krok wstecz", czyli usuwamy 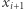 ze ścieżki i cofamy się do
ze ścieżki i cofamy się do 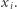 Jeżeli z kolei
Jeżeli z kolei 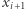 jest większy od któregoś
jest większy od któregoś 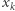 obecnego już na ścieżce, kończymy algorytm i zwracamy TAK, ponieważ ścieżka
obecnego już na ścieżce, kończymy algorytm i zwracamy TAK, ponieważ ścieżka 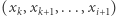 jest rozwojowa dla
jest rozwojowa dla 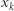 (por. lemat 1). Jeżeli algorytm nie może wykonać już żadnego kroku, zwraca NIE.
(por. lemat 1). Jeżeli algorytm nie może wykonać już żadnego kroku, zwraca NIE.
Przykład 2. Rozważmy następującą instancję problemu: 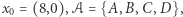 gdzie
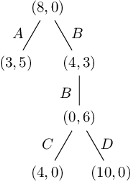
gdzie 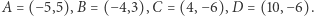 Wówczas stosując powyższy algorytm, otrzymujemy drzewo ścieżek
Wówczas stosując powyższy algorytm, otrzymujemy drzewo ścieżek
Ścieżki 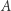 nie da się kontynuować; w
nie da się kontynuować; w 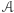 nie ma wektora, który po dodaniu do (3,5) miałby obie współrzędne nieujemne. Z kolei
nie ma wektora, który po dodaniu do (3,5) miałby obie współrzędne nieujemne. Z kolei 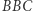 prowadzi do mniejszego punktu. Wreszcie
prowadzi do mniejszego punktu. Wreszcie 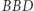 prowadzi do większego.
prowadzi do większego.
Na pierwszy rzut oka algorytm po prostu działa. Okazuje się, że trochę tutaj przemilczeliśmy...
Ustalmy jakieś 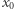 i
i 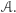 Jest jasne, że jeżeli powyższy algorytm zatrzyma się i zwróci odpowiedź, to jest ona poprawna. Ale czy algorytm na pewno się zatrzymuje?
Jest jasne, że jeżeli powyższy algorytm zatrzyma się i zwróci odpowiedź, to jest ona poprawna. Ale czy algorytm na pewno się zatrzymuje?
Skąd wiadomo, że każda ścieżka zostanie zakończona? Czy może się zdarzyć, że na pewnej ścieżce będziemy otrzymywać coraz inne nieporównywalne wartości, na przykład 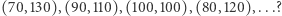 Czy trener może nigdy nie odejść od komputera? Okazuje się, że nie może tak się zdarzyć, a wynika to bezpośrednio z lematu Dicksona.
Czy trener może nigdy nie odejść od komputera? Okazuje się, że nie może tak się zdarzyć, a wynika to bezpośrednio z lematu Dicksona.
Lemat 2 (Dicksona). Niech 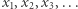 to nieskończony ciąg punktów z
to nieskończony ciąg punktów z 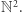 Wówczas istnieją pewne dwa indeksy
Wówczas istnieją pewne dwa indeksy 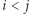 takie, że
takie, że 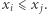
A zatem, gdyby pewna ścieżka nigdy nie została zakończona, to wszystkie pary liczb na niej byłyby nieporównywalne, co przeczyłoby lematowi Dicksona.
Trener już się cieszy, że symulacje na pewno kiedyś się zakończą i wróci na treningi. Ale zaraz, zaraz… udowodniliśmy jedynie, że żadna ścieżka nie jest nieskończona. Czy jednak nie może być tak, że każda ścieżka jest skończona, ale jest nieskończenie wiele coraz dłuższych ścieżek? Wówczas nasz algorytm nigdy by się nie zatrzymał. Okazuje się, że tak nie może być, a odpowiada za to lemat Königa, zastosowany do drzewa konfiguracji symulatora.
Lemat 3 (Königa). Jeżeli w drzewie skierowanym 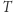 każdy wierzchołek ma skończenie wiele następników i w
każdy wierzchołek ma skończenie wiele następników i w 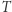 nie ma nieskończonej ścieżki, to
nie ma nieskończonej ścieżki, to 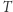 ma skończenie wiele wierzchołków.
ma skończenie wiele wierzchołków.
Podsumowując dowód, na mocy Lematu Dicksona wszystkie ścieżki w drzewie konfiguracji symulatora są skończone, a więc na mocy Lematu Königa ma ono skończenie wiele wierzchołków. Wynika stąd, że algorytm zatrzyma się i, jak już zauważyliśmy, zwróci poprawną odpowiedź.
A jak rozwiązać ten problem w wymiarze większym niż 2? Pomocny okaże się artykuł autorstwa Wojciecha Czerwińskiego "Na granicy możliwości" (Delta 1/2014). Zachęcamy do jego lektury!