Informatyczny kącik olimpijski
Kwadraty liczb naturalnych
W tym odcinku omówimy rozwiązanie zadania "Kwadraty liczb naturalnych", które pojawiło się na finale Zawodów Indywidualnych XIII Młodzieżowej Olimpiady Informatycznej.
Zadanie (Kwadraty liczb naturalnych). Piotr jest zafascynowany kwadratami liczb naturalnych, czyli liczbami: 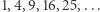 Chłopiec ma przed sobą ciąg
Chłopiec ma przed sobą ciąg 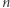 liczb naturalnych
liczb naturalnych 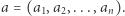 Ile jest takich par liczb naturalnych w ciągu
Ile jest takich par liczb naturalnych w ciągu 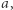 że ich iloczyn jest kwadratem liczby naturalnej?
że ich iloczyn jest kwadratem liczby naturalnej?
Niech 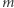 oznacza wartość największej liczby w ciągu
oznacza wartość największej liczby w ciągu 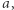 zaś
zaś 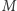 niech oznacza największy iloczyn pary liczb w ciągu
niech oznacza największy iloczyn pary liczb w ciągu 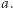
Rozwiązanie 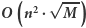
Zacznijmy od rozwiązania, w którym obliczamy iloczyn każdej z 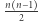 par elementów ciągu
par elementów ciągu  Następnie zliczamy te iloczyny, które są kwadratami liczb naturalnych. Załóżmy, że chcemy sprawdzić, czy
Następnie zliczamy te iloczyny, które są kwadratami liczb naturalnych. Załóżmy, że chcemy sprawdzić, czy  jest kwadratem. W tym celu przeglądamy kwadraty kolejnych liczb naturalnych:
jest kwadratem. W tym celu przeglądamy kwadraty kolejnych liczb naturalnych: 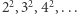 Jeśli trafimy na
Jeśli trafimy na 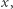 to odpowiedź jest pozytywna. Jeśli trafimy na liczbę większą niż
to odpowiedź jest pozytywna. Jeśli trafimy na liczbę większą niż 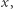 wtedy przerywamy działanie i odpowiedź jest negatywna. Tym sposobem rozważymy
wtedy przerywamy działanie i odpowiedź jest negatywna. Tym sposobem rozważymy 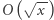 kwadratów. Zatem rozwiązanie działa w czasie
kwadratów. Zatem rozwiązanie działa w czasie 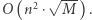
Rozwiązanie 
Przyspieszmy sprawdzanie, czy 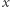 jest kwadratem. Zaaplikujmy algorytm wyszukiwania binarnego na ciągu kwadratów:
jest kwadratem. Zaaplikujmy algorytm wyszukiwania binarnego na ciągu kwadratów: 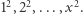 Algorytmy wykona
Algorytmy wykona 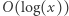 operacji. Całe rozwiązanie działa w czasie
operacji. Całe rozwiązanie działa w czasie 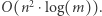
Szkic rozwiązania optymalnego
Zauważmy, że w rozkładzie na czynniki pierwsze kwadratu liczby naturalnej każdy czynnik pierwszy występuje parzyście wiele razy. Zatem iloczyn dwóch liczb jest kwadratem, jeśli zbiory czynników pierwszych występujących nieparzyście wiele razy w rozkładzie obu liczb są takie same. Niech więc 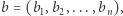 gdzie
gdzie 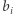 oznacza iloczyn czynników pierwszych, które występują nieparzyście wiele razy w rozkładzie
oznacza iloczyn czynników pierwszych, które występują nieparzyście wiele razy w rozkładzie 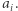 Innymi słowy,
Innymi słowy, 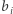 to
to 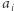 podzielone przez swój największy dzielnik będący kwadratem. Wówczas
podzielone przez swój największy dzielnik będący kwadratem. Wówczas 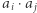 jest kwadratem, jeśli
jest kwadratem, jeśli 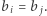 Zatem wynikiem jest liczba par takich samych elementów w ciągu
Zatem wynikiem jest liczba par takich samych elementów w ciągu 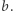
Zliczanie par
Załóżmy przez chwilę, że znamy ciąg 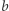 i chcemy policzyć liczbę par elementów o takich samych wartościach. W tym celu wystarczy posortować ciąg niemalejąco. Wówczas elementy o tych samych wartościach znajdą się obok siebie (będą tworzyły bloki). Następnie przeglądamy kolejne bloki elementów i zliczamy pary. W
i chcemy policzyć liczbę par elementów o takich samych wartościach. W tym celu wystarczy posortować ciąg niemalejąco. Wówczas elementy o tych samych wartościach znajdą się obok siebie (będą tworzyły bloki). Następnie przeglądamy kolejne bloki elementów i zliczamy pary. W 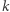 -elementowym bloku można wybrać
-elementowym bloku można wybrać 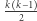 par. Sortowanie realizujemy w czasie
par. Sortowanie realizujemy w czasie 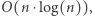 podział na bloki odbywa się w czasie
podział na bloki odbywa się w czasie 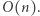 Zatem zliczanie par tych samych elementów w ciągu
Zatem zliczanie par tych samych elementów w ciągu 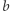 odbywa się w czasie
odbywa się w czasie 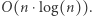
Wyznaczenie ciągu 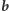 w
w 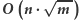
Wartość 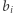 dla każdego
dla każdego 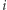 od
od 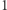 do
do 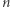 liczymy niezależnie. Początkowo niech
liczymy niezależnie. Początkowo niech 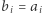 dla każdego
dla każdego 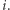 Następnie przeglądamy kolejne kwadraty
Następnie przeglądamy kolejne kwadraty 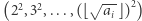 jako kandydatów na dzielniki
jako kandydatów na dzielniki 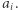 Jeśli rozpatrywany kwadrat jest dzielnikiem
Jeśli rozpatrywany kwadrat jest dzielnikiem 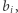 to dzielimy
to dzielimy 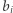 przez ten kwadrat. W ten sposób z rozkładu na czynniki pierwsze usuniemy kwadraty.
przez ten kwadrat. W ten sposób z rozkładu na czynniki pierwsze usuniemy kwadraty.
Wyznaczenie ciągu 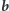 w
w 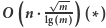
Zauważmy, że nie ma potrzeby przeglądania wszystkich kwadratów. Wystarczy rozważać kwadraty liczb pierwszych 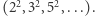 Pamiętajmy o tym, że kwadrat może wielokrotnie występować w rozkładzie na czynniki pierwsze. Wtedy musimy usunąć wszystkie jego wystąpienia. Przykładowo: liczbę
Pamiętajmy o tym, że kwadrat może wielokrotnie występować w rozkładzie na czynniki pierwsze. Wtedy musimy usunąć wszystkie jego wystąpienia. Przykładowo: liczbę 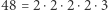 musimy dwukrotnie podzielić przez
musimy dwukrotnie podzielić przez 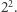 Każda liczba zostanie podzielona co najwyżej
Każda liczba zostanie podzielona co najwyżej 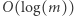 razy. Liczbę liczb pierwszych w przedziale
razy. Liczbę liczb pierwszych w przedziale ![√ --- |[1;⌊ m]⌋](/math/temat/informatyka/algorytmy/2019/07/31/Kwadraty_liczb_naturalnych/7x-0da260290c51d0f7b11a56625522085e8f45db7f-im-33,33,33-FF,FF,FF.gif) szacujemy jako
szacujemy jako 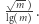 Stąd całkowita złożoność wynosi
Stąd całkowita złożoność wynosi 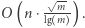
Wyznaczenie ciągu 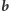 w
w 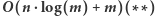
Na początku zliczmy wystąpienia liczb w ciągu 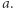 Niech
Niech 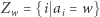 (zbiór indeksów elementów ciągu
(zbiór indeksów elementów ciągu  o wartości
o wartości 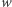 ). Następnie przeglądamy kwadraty liczb pierwszych z przedziału
). Następnie przeglądamy kwadraty liczb pierwszych z przedziału ![[1;m]](/math/temat/informatyka/algorytmy/2019/07/31/Kwadraty_liczb_naturalnych/7x-504287afb17e4629d865db938768ece1242e3458-im-33,33,33-FF,FF,FF.gif) jako potencjalne dzielniki. Załóżmy, że rozpatrujemy kwadrat
jako potencjalne dzielniki. Załóżmy, że rozpatrujemy kwadrat 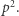 Wiemy, że jest on dzielnikiem:
Wiemy, że jest on dzielnikiem: 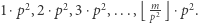 Dla każdej z tych wartości, korzystając z tablicy zliczającej
Dla każdej z tych wartości, korzystając z tablicy zliczającej 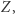 odwołujemy się bezpośrednio do elementów, które są podzielne przez
odwołujemy się bezpośrednio do elementów, które są podzielne przez 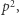 i te elementy dzielimy przez
i te elementy dzielimy przez 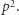 Po zakończeniu otrzymane wartości tworzą ciąg
Po zakończeniu otrzymane wartości tworzą ciąg 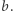 Do każdego elementu ciągu odwołamy się co najwyżej
Do każdego elementu ciągu odwołamy się co najwyżej 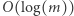 razy. Liczba rozpatrywanych wielokrotności wynosi:
razy. Liczba rozpatrywanych wielokrotności wynosi: 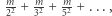 co w sumie wynosi
co w sumie wynosi 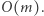 Zatem otrzymaliśmy rozwiązanie działające w czasie
Zatem otrzymaliśmy rozwiązanie działające w czasie 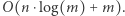
Wyznaczenie ciągu 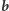 w
w 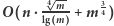
Połączmy dwa poprzednie rozwiązania 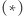 i
i 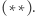 Najpierw, podobnie jak w
Najpierw, podobnie jak w 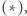 dla każdego elementu ciągu
dla każdego elementu ciągu 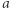 rozważmy jego potencjalne dzielniki (kwadraty liczb pierwszych), nie większe niż
rozważmy jego potencjalne dzielniki (kwadraty liczb pierwszych), nie większe niż 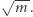 Takich dzielników jest
Takich dzielników jest 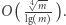 Następnie zaaplikujmy rozwiązanie
Następnie zaaplikujmy rozwiązanie 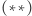 z drobną zmianą. Rozpatrujmy tylko wielokrotności kwadratów liczb pierwszych większych od
z drobną zmianą. Rozpatrujmy tylko wielokrotności kwadratów liczb pierwszych większych od 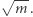 Niestety, tak opisane rozwiązanie nadal wymaga utworzenia tablicy zliczającej rozmiaru
Niestety, tak opisane rozwiązanie nadal wymaga utworzenia tablicy zliczającej rozmiaru 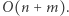 Do implementacji tablicy zliczającej wystarczy użyć tablicy mieszającej (tablicy z haszowaniem) i problem zostaje rozwiązany. Otrzymujemy algorytm, który działa w czasie
Do implementacji tablicy zliczającej wystarczy użyć tablicy mieszającej (tablicy z haszowaniem) i problem zostaje rozwiązany. Otrzymujemy algorytm, który działa w czasie 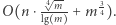 Dowód tego oszacowania pozostawiam Czytelnikowi. Jednocześnie zachęcam do pomyślenia nad lepszym oszacowaniem.
Dowód tego oszacowania pozostawiam Czytelnikowi. Jednocześnie zachęcam do pomyślenia nad lepszym oszacowaniem.