Informatyczny kącik olimpijski
Domino
W tym odcinku omówimy rozwiązanie zadania "Domino", które pojawiło się w 2018 roku w ramach X International Autumn Tournament in Informatics w Szumen, w Bułgarii.
Zadanie (Domino). Zestaw do gry w domino składa się z 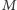 kostek ponumerowanych kolejnymi liczbami naturalnymi od
kostek ponumerowanych kolejnymi liczbami naturalnymi od 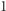 do
do 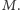 Kostka o numerze
Kostka o numerze 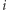 jest opisana za pomocą nieuporządkowanej pary liczb
jest opisana za pomocą nieuporządkowanej pary liczb 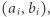 gdzie
gdzie 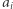 oznacza liczbę kropek narysowanych na jednej połowie, zaś
oznacza liczbę kropek narysowanych na jednej połowie, zaś 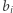 oznacza liczbę kropek narysowanych na drugiej połowie kostki. Wartości
oznacza liczbę kropek narysowanych na drugiej połowie kostki. Wartości 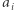 i
i 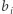 są liczbami całkowitymi z przedziału
są liczbami całkowitymi z przedziału ![].[0;N](/math/temat/informatyka/algorytmy/2019/04/29/Domino/10x-ad488de93d4292dfa2d7c4a110efa46173b1336b-im-33,33,33-FF,FF,FF.gif) W zestawie nie ma dwóch takich samych kostek.
W zestawie nie ma dwóch takich samych kostek.
Trzeba poukładać kostki domina w łańcuchy. Dwie kostki mogą zostać ze sobą zestawione krótszym bokiem, jeśli odpowiednie połowy tych kostek mają tę samą liczbę narysowanych kropek. Naszym zadaniem jest obliczyć, ile minimalnie łańcuchów należy ułożyć, aby każda kostka domina należała do dokładnie jednego łańcucha, oraz podać te łańcuchy.
Rozwiązanie rozpocznijmy od zbudowania grafu 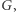 złożonego z
złożonego z 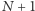 wierzchołków oraz
wierzchołków oraz 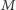 nieskierowanych krawędzi. Wierzchołki ponumerujmy kolejnymi liczbami naturalnymi od 0 do
nieskierowanych krawędzi. Wierzchołki ponumerujmy kolejnymi liczbami naturalnymi od 0 do 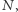 każdej liczbie kropek odpowiada jeden wierzchołek. Ponadto, niech istnieje w
każdej liczbie kropek odpowiada jeden wierzchołek. Ponadto, niech istnieje w 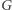 krawędź pomiędzy wierzchołkami
krawędź pomiędzy wierzchołkami 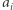 i
i 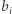 dla każdej kostki domina. Przykładowo, jeśli
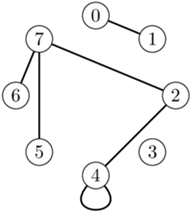
dla każdej kostki domina. Przykładowo, jeśli 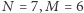 oraz dane są następujące kostki domina:
oraz dane są następujące kostki domina: 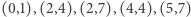 i
i 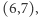 wtedy graf
wtedy graf 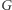 wygląda jak na rysunku obok.
wygląda jak na rysunku obok.
Możemy teraz wyrazić problem w języku teorii grafów.
Problem. Dany jest nieskierowany graf. Jaka jest najmniejsza liczba rozłącznych krawędziowo ścieżek, które pokrywają cały graf?
Oczywiste jest, że żadna ścieżka nie będzie przechodziła pomiędzy dwoma różnymi spójnymi składowymi, dlatego każdą spójną składową możemy rozpatrzyć osobno. Załóżmy zatem, że rozpatrujemy pewną spójną składową. Zastanówmy się, ile może być w niej wierzchołków o stopniu nieparzystym. Po krótkiej chwili namysłu okazuje się, że wierzchołków o stopniu nieparzystym jest parzyście wiele. Jest tak, ponieważ suma stopni wszystkich wierzchołków jest podwojoną liczbą krawędzi (każda krawędź ma dwa końce). Rozważmy zatem dwa przypadki ze względu na liczbę wierzchołków o stopniu nieparzystym.
0 wierzchołków o stopniu nieparzystym
W tym przypadku każdy wierzchołek ma stopień parzysty. W związku z tym zachodzi warunek konieczny i wystarczający na istnienie w grafie cyklu Eulera (cyklu, który przechodzi przez każdą krawędź dokładnie raz). Popularnym algorytmem do znajdowania cyklu Eulera jest algorytm Fleury'ego. Skoro istnieje cykl Eulera, to wszystkie kostki można ułożyć w jeden łańcuch (ścieżka Eulera).
Co najmniej 2 wierzchołki o stopniu nieparzystym
W tym przypadku jest ich parzysta liczba. Niech 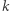 oznacza liczbę wierzchołków o stopniu nieparzystym. Dodajmy do naszego grafu
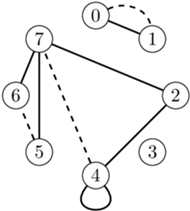
oznacza liczbę wierzchołków o stopniu nieparzystym. Dodajmy do naszego grafu 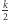 krawędzi łączących wierzchołki o stopniu nieparzystym (każdy wierzchołek o stopniu nieparzystym ma być końcem dokładnie jednej dodanej krawędzi). Dla przykładu opisanego na początku artykułu graf będzie wyglądał, jak na rysunku obok (dodane krawędzie zostały oznaczone przerywaną linią).
krawędzi łączących wierzchołki o stopniu nieparzystym (każdy wierzchołek o stopniu nieparzystym ma być końcem dokładnie jednej dodanej krawędzi). Dla przykładu opisanego na początku artykułu graf będzie wyglądał, jak na rysunku obok (dodane krawędzie zostały oznaczone przerywaną linią).
Otrzymaliśmy multigraf (w multigrafie dwa wierzchołki może łączyć kilka krawędzi), w którym każdy wierzchołek ma parzysty stopień, zatem jest spełniony warunek konieczny i wystarczający na istnienie cyklu Eulera. Znajdźmy więc ten cykl, a następnie usuńmy z niego dodane wcześniej krawędzie. Otrzymane ścieżki opisują kolejne łańcuchy utworzone z kostek domina. W tym przypadku odpowiedzią jest 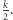
Optymalność rozwiązania
Pozostało nam jeszcze zastanowić się, czy opisane wyżej rozwiązanie jest optymalne. Zauważmy, że każdy wierzchołek o stopniu nieparzystym musi być początkiem lub końcem jakiegoś łańcucha. Takich wierzchołków jest 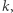 zatem potrzebnych jest przynajmniej
zatem potrzebnych jest przynajmniej 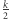 łańcuchów. Opisany wyżej algorytm znajduje dokładnie
łańcuchów. Opisany wyżej algorytm znajduje dokładnie 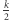 łańcuchów, dlatego jest optymalny.
łańcuchów, dlatego jest optymalny.
Złożoność czasowa
Zbudowany przez nas graf ma rozmiar 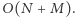 Znajdowanie cyklu Eulera można więc zrealizować w czasie zależnym liniowo od rozmiaru grafu. Całe rozwiązanie działa w czasie
Znajdowanie cyklu Eulera można więc zrealizować w czasie zależnym liniowo od rozmiaru grafu. Całe rozwiązanie działa w czasie