Informatyczny kącik olimpijski
Or
Tym razem omówimy zadanie Or, które pojawiło się w 2018 roku na Junior Balkan Olympiad in Informatics w Timisoarze (Rumunia).
Zadanie. Dana jest liczba całkowita 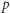 oraz kwadratowa macierz
oraz kwadratowa macierz 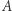 rozmiaru
rozmiaru 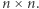 W każdym polu macierzy znajduje się jedna liczba całkowita. Z ilu pól składa się najmniejsza prostokątna podmacierz macierzy
W każdym polu macierzy znajduje się jedna liczba całkowita. Z ilu pól składa się najmniejsza prostokątna podmacierz macierzy 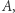 której
której 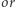 bitowy wszystkich elementów wynosi
bitowy wszystkich elementów wynosi 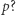
Dla uproszczenia, wartością podmacierzy będziemy nazywali wartość równą 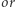 'owi wszystkich liczb w tej podmacierzy.
'owi wszystkich liczb w tej podmacierzy.
Rozwiązanie 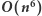
Zaczniemy od najbardziej intuicyjnego pomysłu. Rozwiązanie polega na niezależnym sprawdzeniu każdej podmacierzy i wybraniu tej, która ma wartość 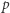 oraz jest najmniejsza. Wszystkich podmacierzy jest
oraz jest najmniejsza. Wszystkich podmacierzy jest 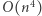 (lewy górny róg możemy wybrać na
(lewy górny róg możemy wybrać na 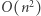 sposobów, podobnie prawy dolny róg możemy wybrać na
sposobów, podobnie prawy dolny róg możemy wybrać na 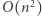 sposobów). Naiwne obliczenie wartości podmacierzy (iterowanie po wszystkich elementach) działa w czasie
sposobów). Naiwne obliczenie wartości podmacierzy (iterowanie po wszystkich elementach) działa w czasie 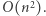 Zatem całe rozwiązanie działa w czasie
Zatem całe rozwiązanie działa w czasie 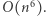
Szybkie obliczanie wartości podmacierzy
Skonstruujemy strukturę danych, która będzie umożliwiała obliczanie wartości dowolnej podmacierzy.
W naiwnym rozwiązaniu iterujemy po każdym polu podmacierzy. Oczywiście takie rozwiązanie jest wolne, dlatego je przyspieszymy. Chcemy, w pewnym sensie, niektóre pola zliczać hurtowo. Zatem obliczymy wartość wszystkich podmacierzy o rozmiarze 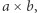 gdzie
gdzie 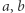 są liczbami postaci
są liczbami postaci 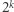 dla
dla 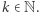 Zauważmy, że takich podmacierzy w całej macierzy
Zauważmy, że takich podmacierzy w całej macierzy 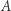 będzie
będzie 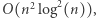 ponieważ w każdym polu jest zaczepionych
ponieważ w każdym polu jest zaczepionych 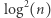 podmacierzy
podmacierzy 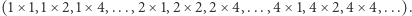

Wartości wyżej opisanych podmacierzy będziemy obliczali od tych, które mają najmniejszą liczbę pól, do tych, które mają największą liczbę pól. Wartość podmacierzy o wymiarach 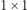 to liczba zapisana w tym polu. Wartość podmacierzy o wymiarach
to liczba zapisana w tym polu. Wartość podmacierzy o wymiarach 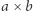 to
to 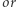 wartości dwóch mniejszych podmacierzy o wymiarach
wartości dwóch mniejszych podmacierzy o wymiarach 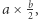 jeśli
jeśli 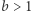 lub
lub 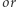 wartości dwóch mniejszych podmacierzy o wymiarach
wartości dwóch mniejszych podmacierzy o wymiarach 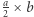 w przeciwnym przypadku. Przykładowo: wartością podmacierzy o wymiarach
w przeciwnym przypadku. Przykładowo: wartością podmacierzy o wymiarach 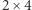 jest
jest 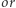 wartości dwóch mniejszych podmacierzy o wymiarach
wartości dwóch mniejszych podmacierzy o wymiarach 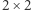 każda.
każda.
Konstrukcja struktury zajmuje 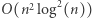 pamięci i odbywa się w czasie
pamięci i odbywa się w czasie 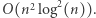
Pozostało nam jeszcze opisanie, w jaki sposób znaleźć wartość dowolnej podmacierzy. Nazwijmy ją 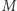 i niech ma wymiary
i niech ma wymiary 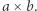 Jej wartość obliczymy na podstawie znanych wartości innych podmacierzy. Ustalmy takie największe
Jej wartość obliczymy na podstawie znanych wartości innych podmacierzy. Ustalmy takie największe 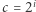 i największe
i największe 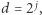 że
że 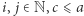 oraz
oraz 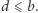 Weźmy takie cztery podmacierze
Weźmy takie cztery podmacierze 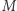 o wymiarach
o wymiarach 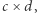 że każde pole
że każde pole 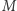 będzie należało do przynajmniej jednej z tych czterech podmacierzy. Wówczas wartością
będzie należało do przynajmniej jednej z tych czterech podmacierzy. Wówczas wartością 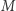 będzie
będzie 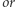 wartości tych czterech podmacierzy.
wartości tych czterech podmacierzy.

Przykład: chcemy obliczyć wartość podmacierzy, której lewe górne pole to 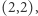 a prawe dolne to
a prawe dolne to 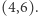 Zauważmy, że tę podmacierz możemy pokryć czterema podmacierzami o wymiarach
Zauważmy, że tę podmacierz możemy pokryć czterema podmacierzami o wymiarach 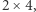 dla których wyniki znamy. Zatem wartością tej podmacierzy jest
dla których wyniki znamy. Zatem wartością tej podmacierzy jest 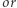 wartości czterech mniejszych podmacierzy.
wartości czterech mniejszych podmacierzy.
Rozwiązanie 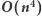
Zauważmy, że dzięki powyższej strukturze danych potrafimy w czasie 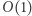 obliczyć wartość dowolnej podmacierzy. Zatem w naturalny sposób możemy przyspieszyć rozwiązanie z
obliczyć wartość dowolnej podmacierzy. Zatem w naturalny sposób możemy przyspieszyć rozwiązanie z 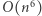 do
do 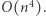 Wystarczy przejrzeć wszystkie
Wystarczy przejrzeć wszystkie 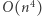 podmacierzy macierzy
podmacierzy macierzy 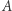 i spośród tych o wartości
i spośród tych o wartości 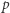 wybrać najmniejszą.
wybrać najmniejszą.
Rozwiązanie 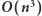
W tym rozwiązaniu iterujemy po każdym przedziale wierszy. W ustalonym przedziale wierszy szukamy najmniejszej podmacierzy o wartości 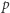 i wysokości równej liczbie wierszy w tym przedziale. Od teraz możemy o tym myśleć jak o problemie jednowymiarowym, ponieważ wysokość jest ustalona. Szukamy najkrótszego fragmentu, który będzie miał wartość
i wysokości równej liczbie wierszy w tym przedziale. Od teraz możemy o tym myśleć jak o problemie jednowymiarowym, ponieważ wysokość jest ustalona. Szukamy najkrótszego fragmentu, który będzie miał wartość 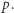 Ten problem możemy rozwiązać za pomocą techniki o nazwie "gąsienica". Na początku ustawiamy dwa wskaźniki (początek i koniec gąsienicy) w pierwszej kolumnie. Następnie symulujemy ruch gąsienicy. Jeśli aktualna wartość jest mniejsza od
Ten problem możemy rozwiązać za pomocą techniki o nazwie "gąsienica". Na początku ustawiamy dwa wskaźniki (początek i koniec gąsienicy) w pierwszej kolumnie. Następnie symulujemy ruch gąsienicy. Jeśli aktualna wartość jest mniejsza od 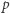 i może jeszcze osiągnąć
i może jeszcze osiągnąć 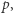 wtedy rozszerzamy gąsienicę o kolejną kolumnę. W przeciwnym przypadku skracamy gąsienicę. W każdym stanie, za pomocą powyżej opisanej struktury, w czasie
wtedy rozszerzamy gąsienicę o kolejną kolumnę. W przeciwnym przypadku skracamy gąsienicę. W każdym stanie, za pomocą powyżej opisanej struktury, w czasie 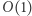 obliczamy wartość aktualnie rozpatrywanej podmacierzy. Dla każdego rozpatrywanego przedziału wierszy gąsienica wykona liniowo wiele ruchów. Wszystkich przedziałów wierszy do rozpatrzenia jest
obliczamy wartość aktualnie rozpatrywanej podmacierzy. Dla każdego rozpatrywanego przedziału wierszy gąsienica wykona liniowo wiele ruchów. Wszystkich przedziałów wierszy do rozpatrzenia jest 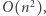 zatem całe rozwiązanie działa w czasie
zatem całe rozwiązanie działa w czasie