Informatyczny kącik olimpijski
Zalesianie
Tym razem omówimy zadanie Zalesianie, które pojawiło się na finale zawodów drużynowych XII Olimpiady Informatycznej Gimnazjalistów.
Zadanie (Zalesianie). Danych jest  wierzchołków ponumerowanych od
wierzchołków ponumerowanych od 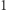 do
do 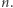 Ciąg
Ciąg 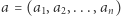 składa się z wartości przyporządkowanych kolejnym wierzchołkom (
składa się z wartości przyporządkowanych kolejnym wierzchołkom ( 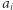 to wartość przyporządkowana
to wartość przyporządkowana 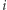 -temu wierzchołkowi). Naszym zadaniem jest zbudować drzewo (spójny, acykliczny graf), przez ustalenie
-temu wierzchołkowi). Naszym zadaniem jest zbudować drzewo (spójny, acykliczny graf), przez ustalenie 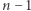 krawędzi między wierzchołkami oraz wybranie wierzchołka, który będzie korzeniem. Chcemy to zrobić w taki sposób, aby zminimalizować współczynnik niezadowolenia. Współczynnik niezadowolenia to maksymalna wartość wyrażenia
krawędzi między wierzchołkami oraz wybranie wierzchołka, który będzie korzeniem. Chcemy to zrobić w taki sposób, aby zminimalizować współczynnik niezadowolenia. Współczynnik niezadowolenia to maksymalna wartość wyrażenia 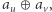 dla takich
dla takich  i
i 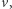 że
że  jest przodkiem
jest przodkiem  (
( 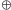 oznacza operację bitową xor).
oznacza operację bitową xor).
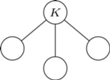
Zastanówmy się najpierw nad strukturą drzewa, które budujemy. Zauważmy, że korzeń jest przodkiem każdego innego wierzchołka w tym drzewie. Zatem, licząc współczynnik niezadowolenia, zawsze będziemy rozpatrywali każdą taką parę wierzchołków  i
i 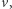 że
że  jest korzeniem drzewa. Okazuje się, że istnieje drzewo, w którym nie ma więcej par wierzchołków pozostających w relacji przodek-potomek. Wystarczy wybrać korzeń oraz połączyć go krawędziami ze wszystkimi pozostałymi wierzchołkami. Obok schemat takiego drzewa
jest korzeniem drzewa. Okazuje się, że istnieje drzewo, w którym nie ma więcej par wierzchołków pozostających w relacji przodek-potomek. Wystarczy wybrać korzeń oraz połączyć go krawędziami ze wszystkimi pozostałymi wierzchołkami. Obok schemat takiego drzewa 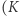 oznacza korzeń).
oznacza korzeń).
Ustaliliśmy już strukturę drzewa. Opiszemy teraz, w jaki sposób wybrać taki korzeń, który będzie minimalizował współczynnik niezadowolenia.
Rozwiązanie 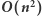
Pierwszy, najbardziej intuicyjny pomysł, polega na naiwnym sprawdzeniu każdego z  sposobów ustalenia korzenia. Dla każdego wierzchołka
sposobów ustalenia korzenia. Dla każdego wierzchołka 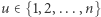 konstruujemy drzewo, którego korzeniem jest
konstruujemy drzewo, którego korzeniem jest  oraz pozostałe wierzchołki są z nim połączone krawędzią. Następnie, dla każdego z tych drzew obliczamy (z definicji) współczynnik niezadowolenia. Spośród otrzymanych wyników wybieramy najmniejszy. Drzew mamy
oraz pozostałe wierzchołki są z nim połączone krawędzią. Następnie, dla każdego z tych drzew obliczamy (z definicji) współczynnik niezadowolenia. Spośród otrzymanych wyników wybieramy najmniejszy. Drzew mamy  (po jednym dla każdego kandydata na korzeń). Obliczenie współczynnika niezadowolenia dla jednego drzewa odbywa się w czasie
(po jednym dla każdego kandydata na korzeń). Obliczenie współczynnika niezadowolenia dla jednego drzewa odbywa się w czasie 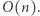 Zatem cały algorytm działa w czasie
Zatem cały algorytm działa w czasie 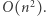
Rozwiązanie 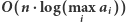
Potraktujmy zapisy binarne elementów ciągu 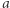 jako słowa nad alfabetem
jako słowa nad alfabetem 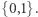 Niech
Niech 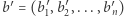 oznacza zapisy binarne kolejnych elementów ciągu
oznacza zapisy binarne kolejnych elementów ciągu  (
( 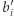 oznacza zapis binarny
oznacza zapis binarny 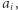 który nie zawiera zer wiodących). Następnie "wyrównajmy" długości słów ciągu
który nie zawiera zer wiodących). Następnie "wyrównajmy" długości słów ciągu  Chcemy otrzymać słowa o takiej samej długości, równej długości najdłuższego słowa w ciągu
Chcemy otrzymać słowa o takiej samej długości, równej długości najdłuższego słowa w ciągu 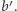 W tym celu wszystkie krótsze słowa należy poprzedzić odpowiednią liczbą zer wiodących. Kolejno otrzymane słowa nazwijmy
W tym celu wszystkie krótsze słowa należy poprzedzić odpowiednią liczbą zer wiodących. Kolejno otrzymane słowa nazwijmy 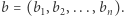
Podobnie jak w rozwiązaniu 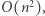 dla każdego potencjalnego korzenia chcemy obliczyć współczynnik niezadowolenia. W istocie, dla każdego
dla każdego potencjalnego korzenia chcemy obliczyć współczynnik niezadowolenia. W istocie, dla każdego 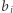 chcemy znaleźć takie
chcemy znaleźć takie 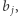 że
że 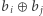 jest maksymalne. Na potrzeby tego artykułu zakładamy, że każdemu
jest maksymalne. Na potrzeby tego artykułu zakładamy, że każdemu 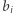 jest przypisana wartość
jest przypisana wartość 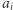 oraz
oraz 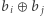 ma wartość
ma wartość 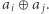
Weźmy 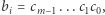 dla którego szukamy takiego
dla którego szukamy takiego 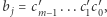 że
że 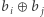 jest maksymalne. Idealnie byłoby, gdyby istniało
jest maksymalne. Idealnie byłoby, gdyby istniało 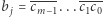 (
( 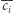 oznacza negację
oznacza negację 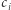 ). Wtedy
). Wtedy 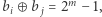 czyli najlepszy możliwy wynik. Ta obserwacja daje nam pewną intuicję. Będziemy wyszukiwali
czyli najlepszy możliwy wynik. Ta obserwacja daje nam pewną intuicję. Będziemy wyszukiwali 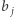 cyfra po cyfrze, w kolejności od najbardziej znaczących do najmniej znaczących. Załóżmy, że mamy już ustalony prefiks
cyfra po cyfrze, w kolejności od najbardziej znaczących do najmniej znaczących. Załóżmy, że mamy już ustalony prefiks 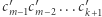 słowa
słowa 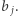 Zastanawiamy się teraz, jaką wartość może mieć
Zastanawiamy się teraz, jaką wartość może mieć 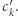 Oczywiście, gdyby
Oczywiście, gdyby 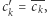 wtedy wynik wzrósłby o
wtedy wynik wzrósłby o 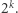 Zatem, jeśli
Zatem, jeśli 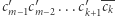 jest prefiksem jakiegoś słowa w ciągu
jest prefiksem jakiegoś słowa w ciągu 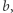 to
to 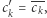 w przeciwnym przypadku
w przeciwnym przypadku 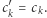 Prosty dowód pozostawiamy Czytelnikowi.
Prosty dowód pozostawiamy Czytelnikowi.
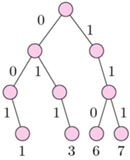
Pozostało nam jeszcze opisać, w jaki sposób dla danego słowa sprawdzać, czy jest ono prefiksem jakiegoś słowa w ciągu 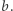 W tym celu zbudujemy drzewo trie nad słowami ciągu
W tym celu zbudujemy drzewo trie nad słowami ciągu 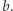 Wyszukiwanie
Wyszukiwanie 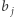 cyfra po cyfrze odpowiada wędrówce w drzewie trie od korzenia do liści. Załóżmy, że w danym kroku ustalamy wartość
cyfra po cyfrze odpowiada wędrówce w drzewie trie od korzenia do liści. Załóżmy, że w danym kroku ustalamy wartość 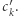 Jeśli wierzchołek, w którym jesteśmy, ma dwóch synów, to poruszamy się krawędzią z etykietą
Jeśli wierzchołek, w którym jesteśmy, ma dwóch synów, to poruszamy się krawędzią z etykietą 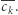 W przeciwnym przypadku nie mamy wyboru - idziemy krawędzią z etykietą
W przeciwnym przypadku nie mamy wyboru - idziemy krawędzią z etykietą 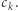 Wędrówkę kończymy w liściu. Kolejno wybierane etykiety krawędzi tworzą szukane
Wędrówkę kończymy w liściu. Kolejno wybierane etykiety krawędzi tworzą szukane 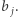
Konstrukcja drzewa trie zajmuje czas 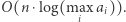 Wyznaczenie
Wyznaczenie 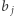 dla danego
dla danego 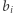 zajmuje czas
zajmuje czas 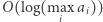 (długość ścieżki od korzenia do liścia). Współczynnik niezadowolenia obliczamy dla każdego z
(długość ścieżki od korzenia do liścia). Współczynnik niezadowolenia obliczamy dla każdego z 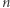 potencjalnych drzew, co w sumie daje
potencjalnych drzew, co w sumie daje 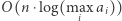 operacji. Zatem cały algorytm działa w czasie
operacji. Zatem cały algorytm działa w czasie 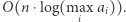
Rozważmy przykład. Niech 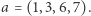 Wówczas
Wówczas 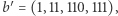
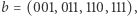 a drzewo trie widać na rysunku obok.
a drzewo trie widać na rysunku obok.