Informatyczny kącik olimpijski
Egzamin
Tym razem omówimy zadanie Egzamin, które pojawiło się w 2010 roku na Junior Balkan Olympiad in Informatics w Szumen (Bułgaria).
Zadanie. Egzamin: Dany jest ciąg 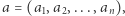 złożony z
złożony z 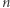 liczb naturalnych, oraz liczba
liczb naturalnych, oraz liczba  Ile jest podciągów ciągu
Ile jest podciągów ciągu 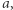 których suma elementów wynosi przynajmniej
których suma elementów wynosi przynajmniej 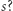 Dla przykładu,
Dla przykładu, 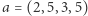 ma
ma 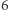 podciągów, które mają sumę przynajmniej
podciągów, które mają sumę przynajmniej 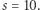 Są to podciągi:
Są to podciągi: 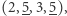
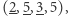
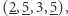
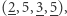
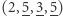 oraz
oraz 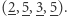
Rozwiązanie 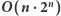
Pomysł, który jako pierwszy nasuwa się na myśl, polega na obliczeniu sumy każdego podciągu, a następnie zliczeniu tych sum, których wartość jest nie mniejsza niż 
Zastanówmy się teraz, jaka jest złożoność opisanego rozwiązania. Ciąg 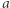 ma
ma 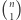 podciągów długości
podciągów długości 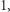
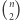 podciągów długości
podciągów długości 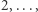 wreszcie
wreszcie 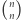 podciągów długości
podciągów długości 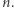 Zatem, suma długości wszystkich podciągów wynosi:
Zatem, suma długości wszystkich podciągów wynosi: 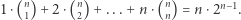 Powyższą sumę można zinterpretować nieco inaczej: każdy z
Powyższą sumę można zinterpretować nieco inaczej: każdy z  elementów ciągu
elementów ciągu 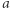 należy do
należy do 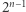 podciągów (dla ustalonego elementu
podciągów (dla ustalonego elementu 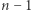 pozostałych elementów tworzy
pozostałych elementów tworzy 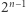 podciągów). Zatem liczba składników we wszystkich sumach wynosi
podciągów). Zatem liczba składników we wszystkich sumach wynosi 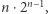 co daje nam złożoność czasową
co daje nam złożoność czasową 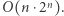
Rozwiązanie 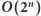
Spróbujmy przyspieszyć powyższe rozwiązanie. Będziemy obliczali sumy podciągów w kolejności niemalejących długości (najpierw podciągi długości jeden, potem długości dwa, trzy, itd.). Załóżmy, że obliczamy sumę podciągu 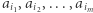 (podciąg ma długość
(podciąg ma długość 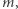 indeksy kolejnych elementów tworzą ciąg
indeksy kolejnych elementów tworzą ciąg 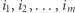 ). Suma elementów tego ciągu to suma podciągu
). Suma elementów tego ciągu to suma podciągu 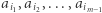 (którą obliczyliśmy wcześniej, ponieważ przeglądamy podciągi od najkrótszych do najdłuższych) powiększona o
(którą obliczyliśmy wcześniej, ponieważ przeglądamy podciągi od najkrótszych do najdłuższych) powiększona o 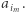 W tym podejściu obliczenie sumy każdego z
W tym podejściu obliczenie sumy każdego z 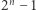 podciągów odbywa się w czasie stałym, co daje nam złożoność czasową
podciągów odbywa się w czasie stałym, co daje nam złożoność czasową 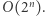
Rozwiązanie 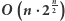
W tym rozwiązaniu skorzystamy z techniki Meet in the middle.
Podzielmy ciąg 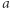 na dwa ciągi równej długości (jeśli długość ciągu jest nieparzysta, wtedy niech pierwszy ciąg zawiera o jeden element więcej): lewy
na dwa ciągi równej długości (jeśli długość ciągu jest nieparzysta, wtedy niech pierwszy ciąg zawiera o jeden element więcej): lewy 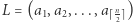 oraz prawy
oraz prawy 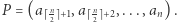 Następnie, dla każdego z nich, obliczmy sumy podciągów. Możemy to zrobić w czasie
Następnie, dla każdego z nich, obliczmy sumy podciągów. Możemy to zrobić w czasie 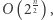 korzystając z algorytmu opisanego w poprzedniej sekcji. Niech
korzystając z algorytmu opisanego w poprzedniej sekcji. Niech 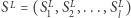 oznacza sumy podciągów
oznacza sumy podciągów 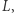 i niech
i niech 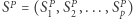 oznacza sumy podciągów
oznacza sumy podciągów 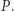
Zauważmy teraz, że dowolny podciąg 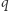 ciągu
ciągu 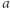 spełnia jeden z trzech poniższych warunków:
spełnia jeden z trzech poniższych warunków:
Warunek (I): wszystkie elementy 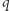 należą do
należą do 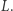
Aby obliczyć liczbę podciągów o sumie przynajmniej 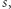 których wszystkie elementy należą do
których wszystkie elementy należą do 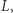 wystarczy zliczyć te elementy ciągu
wystarczy zliczyć te elementy ciągu 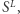 które mają wartość przynajmniej
które mają wartość przynajmniej  Formalnie jest to moc zbioru:
Formalnie jest to moc zbioru: 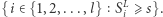 Sprawdzenie tego warunku odbywa się w czasie liniowym od liczby podciągów
Sprawdzenie tego warunku odbywa się w czasie liniowym od liczby podciągów 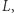 czyli
czyli 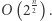
Warunek (II): wszystkie elementy 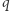 należą do
należą do 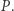
Analogicznie jak warunek (I).
Warunek (III): część elementów 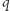 należy do
należy do 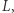 część należy do
część należy do 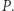
W tym przypadku chcemy obliczyć liczbę takich par 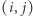 dla
dla 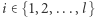 oraz
oraz 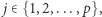 że
że 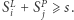 Ten problem rozbijemy na
Ten problem rozbijemy na 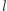 podproblemów. Dla każdego
podproblemów. Dla każdego 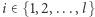 obliczymy, ile jest takich
obliczymy, ile jest takich 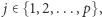 że
że 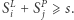
W tym celu posortujmy ciąg 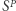 i otrzymany ciąg nazwijmy
i otrzymany ciąg nazwijmy 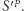 Załóżmy, że obliczamy wynik dla ustalonego
Załóżmy, że obliczamy wynik dla ustalonego 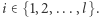 Za pomocą wyszukiwania binarnego szukamy takiego najmniejszego
Za pomocą wyszukiwania binarnego szukamy takiego najmniejszego 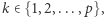 że
że 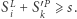 Jeśli takie
Jeśli takie 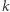 istnieje, wtedy dla każdego
istnieje, wtedy dla każdego 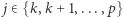 zachodzi
zachodzi 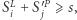 ponieważ
ponieważ 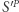 jest niemalejący. Stąd,
jest niemalejący. Stąd, 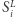 należy do
należy do 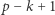 par, które mają sumę przynajmniej
par, które mają sumę przynajmniej  Jeśli zaś takie
Jeśli zaś takie 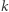 nie istnieje, to
nie istnieje, to 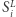 nie tworzy żadnej pary o sumie przynajmniej
nie tworzy żadnej pary o sumie przynajmniej 
Faza sortowania zajmuje czas 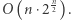 Wyznaczenie liczby poprawnych par, dla ustalonej wartości, za pomocą wyszukiwania binarnego zajmuje czas
Wyznaczenie liczby poprawnych par, dla ustalonej wartości, za pomocą wyszukiwania binarnego zajmuje czas 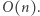 Wszystkich wartości do sprawdzenia jest
Wszystkich wartości do sprawdzenia jest 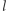 (
( 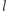 jest rzędu
jest rzędu 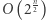 ), co daje całkowitą złożoność
), co daje całkowitą złożoność 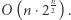
Przykład. Prześledźmy opisany algorytm na przykładzie ciągu 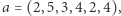 w którym szukamy liczby podciągów o sumie przynajmniej
w którym szukamy liczby podciągów o sumie przynajmniej  Najpierw dzielimy ciąg
Najpierw dzielimy ciąg  na dwa ciągi i dla każdego z nich obliczamy sumy wszystkich jego podciągów:
na dwa ciągi i dla każdego z nich obliczamy sumy wszystkich jego podciągów:

Z warunku (I) mamy 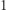 podciąg, z warunku (II) również
podciąg, z warunku (II) również 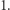 Przechodzimy do warunku (III). Najpierw sortujemy
Przechodzimy do warunku (III). Najpierw sortujemy 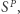 otrzymując
otrzymując 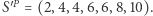 Teraz wyznaczamy wyniki dla kolejnych elementów
Teraz wyznaczamy wyniki dla kolejnych elementów 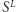 :
: 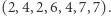 Ostatecznym wynikiem jest:
Ostatecznym wynikiem jest:
