Jak proste problemy stały się trudne
Dawno, dawno temu, wierzono, że fundamentalne zasady rządzące światem są proste. Kiedy dziedzina nauki, zwana obecnie informatyką, dopiero raczkowała, naukowcy byli przekonani, że dla każdego problemu obliczeniowego można znaleźć efektywny algorytm, o ile poświęci się na to wystarczająco dużo czasu, kredy oraz kawy. Pojęcie "efektywnego algorytmu" oznaczało początkowo algorytm o czasie działania proporcjonalnym do rozmiaru danych wejściowych, ale i algorytmy o złożoności obliczeniowej 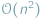 czy
czy 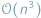 były do zaakceptowania.
były do zaakceptowania.
Pojawiły się jednak problemy, których pomimo wielu lat badań i hektolitrów wypitej kawy nikt nie umiał rozwiązać lepiej, niż generując wszystkie potencjalne rozwiązania i wybierając najlepsze z nich. Czas działania takich algorytmów jest zazwyczaj wykładniczy, zatem dla dużych danych działają one zdecydowanie wolniej niż te o złożoności wielomianowej. Do trudnych problemów należały:
- Pokrycie Wierzchołkowe: mając dany graf, znajdź najmniejszy podzbiór wierzchołków, stykający się z każdą krawędzią.
- Cykl Hamiltona: mając dany graf, rozstrzygnij, czy istnieje cykl odwiedzający każdy wierzchołek dokładnie raz.
- Spełnialność Formuł (SAT): mając daną formułę logiczną, złożoną ze zmiennych przyjmujących wartości prawda/fałsz oraz operatorów AND, OR, NOT, rozstrzygnij, czy można przypisać zmiennym takie wartości, aby formuła była prawdziwa.

Naukowcy zaczęli rozumieć to zjawisko lepiej na początku lat 70. Choć nie udało się efektywnie rozwiązać ani jednego z "trudnych" problemów, ani też wykluczyć istnienia algorytmów wielomianowych, udowodniono, że prawie wszystkie znane trudne problemy są równoważne na mocy wielomianowych redukcji pomiędzy nimi. Powstała teoria NP-trudności wyjaśniała, że efektywne rozwiązanie dowolnego z nich pociąga istnienie szybkich algorytmów dla pozostałych. Zamiast zastanawiać się nad setkami różnych problemów niezależnie, naukowcy zrozumieli, że "jądro" trudności jest takie samo. Choć dalej nie wiemy, czy da się je rozwiązać wielomianowo, całe zagadnienie sprowadza się do jednego kluczowego pytania: "czy P 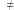 NP?". Świat znów stał się prosty.
NP?". Świat znów stał się prosty.
Teoria NP-trudności okazuje się jednak czasem zbyt "grubo ciosana", chociażby dla uczestników Olimpiady Informatycznej. Powiedzmy, że na zawodach pojawia się zadanie "rozstrzygnij, czy w danym zbiorze liczb naturalnych istnieją takie 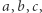 że
że 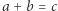 ". Najprostszy algorytm przegląda wszystkie trójki liczb i działa w czasie
". Najprostszy algorytm przegląda wszystkie trójki liczb i działa w czasie 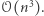 Znajomość podstawowych struktur danych pozwala na poprawę czasu działania do
Znajomość podstawowych struktur danych pozwala na poprawę czasu działania do 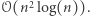 Ale czy da się poprawiać dalej, np. do
Ale czy da się poprawiać dalej, np. do 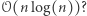 Inny problem: "mając dane dwa ciągi liczb, znajdź ich najdłuższy wspólny podciąg (niekoniecznie spójny)". Programowanie dynamiczne pozwala rozwiązać go w czasie
Inny problem: "mając dane dwa ciągi liczb, znajdź ich najdłuższy wspólny podciąg (niekoniecznie spójny)". Programowanie dynamiczne pozwala rozwiązać go w czasie 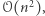 ale skąd wiadomo, że nie da się lepiej?
ale skąd wiadomo, że nie da się lepiej?
Pierwszy zdefiniowany wyżej problem nazywa się 3SUM i, jako że ma rozwiązanie wielomianowe, teoria NP-trudności nie mówi nam nic o ograniczeniach dolnych na złożoność algorytmu. 3SUM okazuje się istotny w geometrii obliczeniowej i w latach 90. zastanawiano się, czy da się go rozwiązać w czasie np. 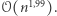 Jako że zapasy kawy przeznaczonej na badania zaczynały się kurczyć, postawiono nową hipotezę, że nie istnieje algorytm podkwadratowy dla 3SUM. Z hipotezy wynikało, że nie istnieją podkwadratowe algorytmy dla wielu innych zagadnień, np. obliczania sumarycznej powierzchni
Jako że zapasy kawy przeznaczonej na badania zaczynały się kurczyć, postawiono nową hipotezę, że nie istnieje algorytm podkwadratowy dla 3SUM. Z hipotezy wynikało, że nie istnieją podkwadratowe algorytmy dla wielu innych zagadnień, np. obliczania sumarycznej powierzchni 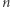 figur na płaszczyźnie. Jednak w przeciwieństwie do hipotezy P
figur na płaszczyźnie. Jednak w przeciwieństwie do hipotezy P 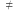 NP nieznane były żadne szokujące implikacje odrzucenia hipotezy 3SUM, toteż nie zyskała ona podobnego zainteresowania.
NP nieznane były żadne szokujące implikacje odrzucenia hipotezy 3SUM, toteż nie zyskała ona podobnego zainteresowania.
W międzyczasie rozwijała się teoria algorytmów wykładniczych. Postawiono wiele pytań typu "dla Cyklu Hamiltona znamy algorytm o złożoności 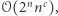 ale czy można to poprawić do
ale czy można to poprawić do 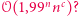 "
"
Aby wykluczyć istnienie szybszych algorytmów wykładniczych, potrzebowano jeszcze silniejszych hipotez niż P 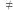 NP, ale takich, których obalenie byłoby wielkim szokiem dla nauki - inaczej trudno przekonać innych do wiary w nową hipotezę. Jedną z nich jest Strong Exponential Time Hypothesis (SETH), która w uproszczeniu głosi, że problemu SAT nie tylko nie da się rozwiązać wielomianowo, ale nawet złożoność
NP, ale takich, których obalenie byłoby wielkim szokiem dla nauki - inaczej trudno przekonać innych do wiary w nową hipotezę. Jedną z nich jest Strong Exponential Time Hypothesis (SETH), która w uproszczeniu głosi, że problemu SAT nie tylko nie da się rozwiązać wielomianowo, ale nawet złożoność 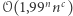 jest nieosiągalna. W oparciu o tę hipotezę (lub jej słabszą wersję) uzasadniono, że różne znane algorytmy wykładnicze są optymalne i dopóki nie zrozumiemy lepiej problemu SAT, nie warto już nad nimi pracować. Zaczęliśmy widzieć więcej, a świat się znowu trochę uprościł.
jest nieosiągalna. W oparciu o tę hipotezę (lub jej słabszą wersję) uzasadniono, że różne znane algorytmy wykładnicze są optymalne i dopóki nie zrozumiemy lepiej problemu SAT, nie warto już nad nimi pracować. Zaczęliśmy widzieć więcej, a świat się znowu trochę uprościł.

Wróćmy do świata wielomianowego i spójrzmy na następujący problem Orthogonal Vectors:
Problem. Mając dane 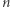 (krótkich) wektorów, rozstrzygnij, czy istnieje wśród nich para wektorów prostopadłych (czyli o iloczynie skalarnym 0).
(krótkich) wektorów, rozstrzygnij, czy istnieje wśród nich para wektorów prostopadłych (czyli o iloczynie skalarnym 0).
Oczywiście, łatwo go rozwiązać, sprawdzając wszystkie pary wektorów i - jak zapewne Czytelnik już się domyśla - nie wiemy, czy da się to zrobić sprytniej. W roku 2005 opublikowano zaskakującą redukcję, z której wynika, że algorytm dla Orthogonal Vectors o złożoności 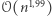 pociągałby algorytm dla SAT o złożoności
pociągałby algorytm dla SAT o złożoności 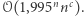 Teorie złożoności wielomianowej i wykładniczej zaczęły się przenikać. Następnie pokazano redukcję z problemu Orthogonal Vectors do wspomnianego wcześniej problemu najdłuższego podciągu. Oznacza to, że kwadratowy algorytm obliczania najdłuższego podciągu (znany od lat 60. i wykorzystywany intensywnie w biologii obliczeniowej) jest optymalny przy założeniu SETH.
Teorie złożoności wielomianowej i wykładniczej zaczęły się przenikać. Następnie pokazano redukcję z problemu Orthogonal Vectors do wspomnianego wcześniej problemu najdłuższego podciągu. Oznacza to, że kwadratowy algorytm obliczania najdłuższego podciągu (znany od lat 60. i wykorzystywany intensywnie w biologii obliczeniowej) jest optymalny przy założeniu SETH.
Badacze zachęceni tymi odkryciami doszli do wniosku, że pół wieku po narodzinach teorii NP-trudności informatyka jest już "gotowa", by stworzyć teorię dokładnej złożoności wielomianowej. Pojawiły się kolejne redukcje z problemów Orthogonal Vectors i 3SUM. W porównaniu do klasycznej teorii złożoności "krajobraz" redukcji okazał się bardziej skomplikowany: zamiast jednej hipotezy mamy ich kilka (choć niektóre są powiązane), a zamiast równoważności pomiędzy problemami często znamy jedynie implikacje w jedną stronę. Pewne miejsca w tym krajobrazie udało się już zrozumieć lepiej. Na przykład, dla każdego z poniższych problemów znany jest algorytm o złożoności 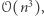 a znalezienie algorytmu o złożoności
a znalezienie algorytmu o złożoności 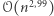 pociągałoby postęp dla wszystkich pozostałych:
pociągałoby postęp dla wszystkich pozostałych:
- Obliczanie najkrótszych ścieżek pomiędzy wszystkimi parami wierzchołków w grafie.
- Szukanie w grafie trójkąta o ujemnej sumie wag krawędzi.
- Rozstrzyganie, czy dana funkcja zadaje metrykę.
- Obliczanie promienia grafu (takiego najmniejszego
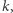 że istnieje wierzchołek
że istnieje wierzchołek 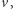 z którego odległość do wszystkich innych jest nie większa niż
z którego odległość do wszystkich innych jest nie większa niż 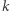 ).
).
Czy faktycznie teoria dokładnej złożoności jest bardziej skomplikowana niż teoria NP-trudności, czy też najbliższe lata przyniosą kolejny przełom i kolejne uproszczenie świata? To pytanie jest obecnie obiektem intensywnych badań, m.in. na Uniwersytecie Warszawskim. Czytelników zainteresowanych naszym stanem wiedzy w tej dziedzinie odsyłam do artykułu Virginii V. Williams Hardness of Easy Problems: Basing Hardness on Popular Conjectures such as the Strong Exponential Time Hypothesis.