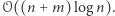Informatyczny kącik olimpijski
Problem (MAX, +) kontratakuje
Tym razem wyjątkowo nie omówimy żadnego nowego zadania. Wrócimy za to do problemu przedstawionego w  w artykule Złośliwy problem
w artykule Złośliwy problem  i kubełkowe struktury danych...
i kubełkowe struktury danych...
Problem ten wygląda następująco: Dany jest ciąg złożony z  liczb całkowitych
liczb całkowitych  Na tym ciągu chcemy wykonywać dwa typy operacji: (1) przypisanie wartości
Na tym ciągu chcemy wykonywać dwa typy operacji: (1) przypisanie wartości 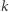 każdemu elementowi ciągu o indeksie z przedziału
każdemu elementowi ciągu o indeksie z przedziału ![|[i.. j]](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/4x-9f0814d2d681d2a4a373c3c31fc16ba211acb834-im-33,33,33-FF,FF,FF.gif) i wartości mniejszej niż
i wartości mniejszej niż 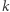 (operacja
(operacja 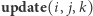 ) oraz (2) zapytanie o sumę elementów ciągu o indeksach z przedziału
) oraz (2) zapytanie o sumę elementów ciągu o indeksach z przedziału ![[i.. j]](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/7x-9f0814d2d681d2a4a373c3c31fc16ba211acb834-im-33,33,33-FF,FF,FF.gif) (operacja
(operacja 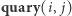 ).
).
W oryginalnym artykule przedstawiona była struktura danych, która 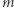 takich operacji potrafi wykonać w czasie
takich operacji potrafi wykonać w czasie 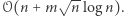 Autor tamtego opracowania (Wojciech Śmietanka) zorganizował wówczas konkurs na poprawę tej złożoności, który udało mi się wtedy wygrać, uzyskując wynik
Autor tamtego opracowania (Wojciech Śmietanka) zorganizował wówczas konkurs na poprawę tej złożoności, który udało mi się wtedy wygrać, uzyskując wynik 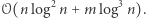 Niedawno w algorytmicznej społeczności pojawił się jeszcze lepszy pomysł, który przedstawię w dzisiejszym kąciku. Nie dość, że rozwiązuje on nasz problem w czasie
Niedawno w algorytmicznej społeczności pojawił się jeszcze lepszy pomysł, który przedstawię w dzisiejszym kąciku. Nie dość, że rozwiązuje on nasz problem w czasie 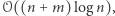 to jeszcze korzysta wyłącznie ze zwykłego drzewa przedziałowego! (Choć to, jakie konkretnie informacje będziemy przechowywać w każdym przedziale bazowym, jest - według mnie - dość nieintuicyjne.)
to jeszcze korzysta wyłącznie ze zwykłego drzewa przedziałowego! (Choć to, jakie konkretnie informacje będziemy przechowywać w każdym przedziale bazowym, jest - według mnie - dość nieintuicyjne.)
Przejdźmy do sedna. W każdym wierzchołku drzewa przedziałowego będziemy utrzymywać następujące informacje o elementach zawartych w jego przedziale bazowym: 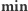 - minimalna wartość wśród elementów z przedziału;
- minimalna wartość wśród elementów z przedziału; 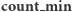 - liczba elementów o wartości równej
- liczba elementów o wartości równej 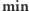 ;
; 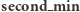 - najmniejsza wartość elementu różna od
- najmniejsza wartość elementu różna od 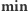 lub nieskończoność, jeśli wszystkie wartości w przedziale są równe;
lub nieskończoność, jeśli wszystkie wartości w przedziale są równe; 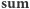 - suma wartości elementów;
- suma wartości elementów;  - wartość
- wartość 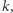 o jaką należy zaktualizować dzieci przedziału bazowego, aby wartości w nich przechowywane stały się aktualne, lub null, gdy wartości w dzieciach są aktualne.
o jaką należy zaktualizować dzieci przedziału bazowego, aby wartości w nich przechowywane stały się aktualne, lub null, gdy wartości w dzieciach są aktualne.
Po pierwsze, zachęcamy Czytelnika do przekonania się, że z aktualnych wartości dla dzieci przedziału bazowego możemy odzyskać wartości dla ojca. Następnie razem przeanalizujmy, w jaki sposób aktualizujemy konkretny przedział bazowy o nową wartość 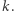 Jeśli
Jeśli 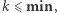 to nie robimy nic. Nawet najmniejsza wartość nie zostanie zmieniona na
to nie robimy nic. Nawet najmniejsza wartość nie zostanie zmieniona na 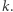 Jeśli
Jeśli 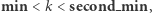 to wszystkie elementy o wartości
to wszystkie elementy o wartości 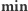 zamienią się na elementy o wartości
zamienią się na elementy o wartości 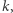 czyli przypisujemy
czyli przypisujemy 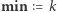 oraz
oraz 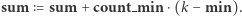 Przypisujemy również
Przypisujemy również 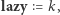 być może nadpisując mniejszą wartość
być może nadpisując mniejszą wartość 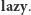 Jeśli
Jeśli 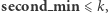 to rekurencyjnie aktualizujemy dzieci przedziału bazowego i w czasie stałym odzyskujemy z nich informacje o ojcu.
to rekurencyjnie aktualizujemy dzieci przedziału bazowego i w czasie stałym odzyskujemy z nich informacje o ojcu.

Otrzymując zapytanie o przedział ![[i.. j],](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/1x-cac23771e4811b10d960f5c7a3869fedba5716c9-im-33,33,33-FF,FF,FF.gif) rekurencyjnie rozkładamy go na przedziały bazowe. Jeśli w rekurencji natrafimy na przedział z wartością
rekurencyjnie rozkładamy go na przedziały bazowe. Jeśli w rekurencji natrafimy na przedział z wartością 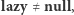 to - jak wyżej - aktualizujemy jego dzieci. Następnie można odzyskać sumę albo zaktualizować owe przedziały bazowe i odzyskać wartości ich przodków w drzewie.
to - jak wyżej - aktualizujemy jego dzieci. Następnie można odzyskać sumę albo zaktualizować owe przedziały bazowe i odzyskać wartości ich przodków w drzewie.
Sama poprawność algorytmu jest dość oczywista. Jednak skąd bierze się tak dobra złożoność czasowa? Nietrudno skonstruować przykład, w którym jedna operacja 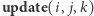 zajmie czas
zajmie czas 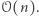 Problemem są zejścia rekurencyjne, gdy
Problemem są zejścia rekurencyjne, gdy 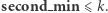 Oznaczmy ich liczbę przez
Oznaczmy ich liczbę przez  Poza nimi wszystko działa jak w zwykłych drzewach przedziałowych, więc nasz algorytm działa w czasie
Poza nimi wszystko działa jak w zwykłych drzewach przedziałowych, więc nasz algorytm działa w czasie 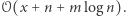
Przejdźmy do dokładniejszej analizy algorytmu. Weźmy przedział bazowy 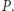 Jeśli w jakimś nadprzedziale przypisaliśmy wartość
Jeśli w jakimś nadprzedziale przypisaliśmy wartość 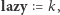 to w nim całym była tylko jedna wartość nie większa niż
to w nim całym była tylko jedna wartość nie większa niż 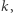 w szczególności
w szczególności 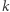 było mniejsze niż
było mniejsze niż 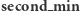 dla
dla 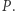 Dowodzi to, iż wartości
Dowodzi to, iż wartości 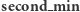 zawsze pozostają aktualne. Z tego powodu przy propagowaniu wartości
zawsze pozostają aktualne. Z tego powodu przy propagowaniu wartości 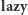 nie natrafimy na przypadek
nie natrafimy na przypadek 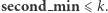 Całe
Całe 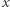 pochodzi więc z aktualizacji przedziałów bazowych o nowe wartości
pochodzi więc z aktualizacji przedziałów bazowych o nowe wartości 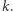
Aby oszacować wartość  w terminach
w terminach 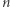 oraz
oraz 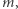 wprowadzimy pojęcie potencjału. Dla danego przedziału bazowego możemy policzyć, ile jest w nim różnych wartości. Potencjałem dla ciągu nazwijmy sumę tych wartości, liczoną po wszystkich przedziałach bazowych. Potencjał ten będzie największy, jeśli wszystkie wartości w ciągu będą różne. Będzie on wtedy wynosił tyle, ile suma długości przedziałów bazowych, czyli
wprowadzimy pojęcie potencjału. Dla danego przedziału bazowego możemy policzyć, ile jest w nim różnych wartości. Potencjałem dla ciągu nazwijmy sumę tych wartości, liczoną po wszystkich przedziałach bazowych. Potencjał ten będzie największy, jeśli wszystkie wartości w ciągu będą różne. Będzie on wtedy wynosił tyle, ile suma długości przedziałów bazowych, czyli 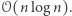

Najpierw zastanówmy się, kiedy nasz potencjał może się zwiększyć za względu na dany przedział bazowy 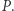 Przy operacji
Przy operacji 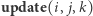 zbiór wartości w
zbiór wartości w 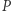 może się powiększyć co najwyżej o jeden element - o element o wartości
może się powiększyć co najwyżej o jeden element - o element o wartości 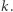 Aby tak się stało, musi zachodzić
Aby tak się stało, musi zachodzić 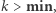 w przeciwnym razie żaden element w
w przeciwnym razie żaden element w 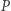 nie otrzyma nowej wartości
nie otrzyma nowej wartości 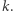 Ponadto przedział
Ponadto przedział ![|[i.. j]](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/8x-6d9a435513e7bc7a7e0a2019f513e0c0d5f1a5a7-im-33,33,33-FF,FF,FF.gif) nie może zawierać całego
nie może zawierać całego 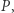 w przeciwnym razie usuniemy wartość
w przeciwnym razie usuniemy wartość 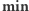 ze zbioru wartości z
ze zbioru wartości z 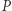 i potencjał się nie zwiększy. Liczba przedziałów bazowych, które przecinają się z
i potencjał się nie zwiększy. Liczba przedziałów bazowych, które przecinają się z ![|[i.. j],](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/12x-6d9a435513e7bc7a7e0a2019f513e0c0d5f1a5a7-im-33,33,33-FF,FF,FF.gif) a nie są zawarte w
a nie są zawarte w ![[i.. j],](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/13x-6d9a435513e7bc7a7e0a2019f513e0c0d5f1a5a7-im-33,33,33-FF,FF,FF.gif) wynosi
wynosi 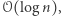 a są to dokładnie te przedziały, które odwiedzamy rekurencyjnie, rozkładając
a są to dokładnie te przedziały, które odwiedzamy rekurencyjnie, rozkładając ![[i.. j]](/math/temat/informatyka/algorytmy/2018/08/26/Problem_MAX_kontratakuje/15x-6d9a435513e7bc7a7e0a2019f513e0c0d5f1a5a7-im-33,33,33-FF,FF,FF.gif) na przedziały bazowe. Ze względu na każdy z tych
na przedziały bazowe. Ze względu na każdy z tych 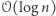 przedziałów potencjał zwiększy się o co najwyżej jeden.
przedziałów potencjał zwiększy się o co najwyżej jeden.
Nasz potencjał na początku wynosił co najwyżej 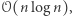 a podczas każdej z
a podczas każdej z 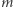 operacji wzrośnie o co najwyżej
operacji wzrośnie o co najwyżej 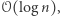 a więc może też zmaleć co najwyżej
a więc może też zmaleć co najwyżej 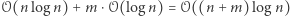 razy.
razy.
Wróćmy do naszego problematycznego przypadku, czyli gdy w aktualizowanym o wartość 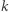 przedziale zachodzi
przedziale zachodzi 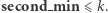 Wszystkie elementy o wartościach
Wszystkie elementy o wartościach 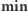 oraz
oraz 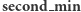 będę po aktualizacji miały wartość równą
będę po aktualizacji miały wartość równą 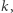 czyli liczba różnych wartości w aktualizowanym przedziale bazowym zmaleje i zmaleje też potencjał. W ten sposób ograniczyliśmy
czyli liczba różnych wartości w aktualizowanym przedziale bazowym zmaleje i zmaleje też potencjał. W ten sposób ograniczyliśmy 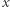 przez
przez 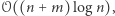 a cały algorytm, tak jak postulowaliśmy, zadziała w czasie
a cały algorytm, tak jak postulowaliśmy, zadziała w czasie