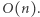Ciągi i łańcuchy
Tym razem omówimy dwa zadania z IX International Autumn Tournament in Informatics, który odbył się w listopadzie 2017 roku w Szumem w Bułgarii.
Zadanie (Ciągi). Dane są trzy dodatnie liczby całkowite 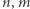 i
i 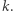 Należy obliczyć liczbę niemalejących ciągów długości
Należy obliczyć liczbę niemalejących ciągów długości 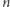 o wartościach będących liczbami całkowitymi z przedziału
o wartościach będących liczbami całkowitymi z przedziału ![[1;m],](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/4x-37311dca1c61ed076dc74a8482b09f3b4583b8d4-im-33,33,33-FF,FF,FF.gif) w których żadna wartość nie występuje więcej niż
w których żadna wartość nie występuje więcej niż 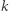 razy. Przykład: dla
razy. Przykład: dla 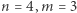 i
i 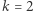 poprawną odpowiedzią jest
poprawną odpowiedzią jest 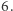 Poprawnymi ciągami są:
Poprawnymi ciągami są: 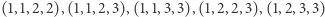 oraz
oraz 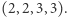
Rozwiązanie 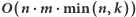
W rozwiązaniu skorzystamy z techniki programowania dynamicznego. Niech ![P[i][ j]D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/2x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) oznacza liczbę niemalejących ciągów długości
oznacza liczbę niemalejących ciągów długości 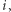 złożonych z liczb całkowitych z przedziału
złożonych z liczb całkowitych z przedziału ![[1; j],](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/4x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) w których żadna wartość nie występuje więcej niż
w których żadna wartość nie występuje więcej niż 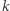 razy. Łatwo zauważyć, że:
razy. Łatwo zauważyć, że:
![P[0][ j]=1 D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/7x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) dla
dla ![| j∈ [1;m],](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/8x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) jest tylko jeden pusty ciąg;
jest tylko jeden pusty ciąg;![P[i][1]=1 D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/10x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) dla
dla ![i ∈[1;k]](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/11x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) ;
;![P[i][1]=0 D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/13x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) dla
dla ![|i∈ [k+ 1;n].](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/14x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif)
Zastanówmy się teraz, jak obliczyć wartość ![P[i][ j] D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/15x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) dla pozostałych par
dla pozostałych par 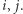 W ciągach niemalejących elementy o tych samych wartościach tworzą spójny przedział. W szczególności wartości
W ciągach niemalejących elementy o tych samych wartościach tworzą spójny przedział. W szczególności wartości 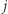 tworzą spójny przedział długości
tworzą spójny przedział długości ![l∈ [0,min(i,k)].](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/18x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) Zatem, otrzymujemy ogólny wzór:
Zatem, otrzymujemy ogólny wzór:
![mini,k P[i][ j]=QDP[i−l][ j−1]. D l0](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/19x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-dm-33,33,33-FF,FF,FF.gif)
Odpowiedzią w zadaniu jest wartość ![P[n][m]. D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/20x-d95ea91defa8fa0f7f5e4d29d69b696e486a3aad-im-33,33,33-FF,FF,FF.gif) Rozwiązanie działa w czasie
Rozwiązanie działa w czasie 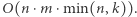
Rozwiązanie 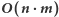
Powyższy wzór możemy zapisać równoważnie jako:
- dla
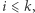
![ii P[i][ j]=QDP[i−l][ j−1]=DP[i][ j−1]+QDP[i−l][ j−1]= D l0l1 i−1 P[i][ j−1]+QDP[i−1−l][ j−1]= = D l0 P[i][ j−1]+DP[i−1][ j] = D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/4x-c7167c48f10bf731e78b5642222a4869004dc670-dm-33,33,33-FF,FF,FF.gif)
- dla
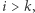
![kk P[i][ j]=QDP[i−l][ j−1]=DP[i][ j−1]+QDP[i−l][ j−1]= D l0l1 k−1 P[i][ j−1]+QDP[i−1−l][ j−1]= = D l0 P[i][ j−1]+DP[i−1][ j]−DP[i−1−k][ j−1] = D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/7x-c7167c48f10bf731e78b5642222a4869004dc670-dm-33,33,33-FF,FF,FF.gif)
Zauważmy, że obliczenie wartości ![[i][ j] D](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/8x-c7167c48f10bf731e78b5642222a4869004dc670-im-33,33,33-FF,FF,FF.gif) dla dowolnych
dla dowolnych 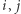 zajmuje czas stały. Zatem całe rozwiązanie działa w czasie
zajmuje czas stały. Zatem całe rozwiązanie działa w czasie 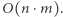
Zadanie (Łańcuchy). Dany jest ciąg liczb całkowitych 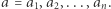 Łańcuch rozpoczynający się na
Łańcuch rozpoczynający się na 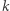 -tej pozycji powstaje w niżej opisany sposób. Znajdujemy pierwszy większy element na prawo od
-tej pozycji powstaje w niżej opisany sposób. Znajdujemy pierwszy większy element na prawo od 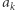 i oznaczamy go przez
i oznaczamy go przez 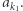 Następnie znajdujemy pierwszy większy element na prawo od
Następnie znajdujemy pierwszy większy element na prawo od 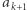 i oznaczmy go przez
i oznaczmy go przez 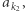 itd. W ten sposób, dla ustalonego
itd. W ten sposób, dla ustalonego 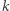 otrzymujemy łańcuch
otrzymujemy łańcuch 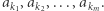 W zadaniu należy dla każdego
W zadaniu należy dla każdego 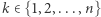 znaleźć długość łańcucha rozpoczynającego się na
znaleźć długość łańcucha rozpoczynającego się na 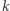 -tej pozycji. Przykład: dla
-tej pozycji. Przykład: dla 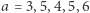 wynikiem jest
wynikiem jest 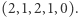
Rozwiązanie 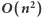
Najprostsze rozwiązanie polega na wygenerowaniu dla każdego 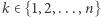 łańcucha rozpoczynającego się na
łańcucha rozpoczynającego się na 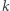 -tej pozycji (zgodnie z opisem w treści zadania) i wypisaniu jego długości. Wyznaczenie łańcucha dla każdej pozycji zajmuje
-tej pozycji (zgodnie z opisem w treści zadania) i wypisaniu jego długości. Wyznaczenie łańcucha dla każdej pozycji zajmuje 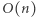 operacji (musimy przeiterować się po całym ciągu). Zatem całe rozwiązanie działa w czasie
operacji (musimy przeiterować się po całym ciągu). Zatem całe rozwiązanie działa w czasie 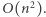
Rozwiązanie 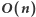
Niech ![|F[k]](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/2x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif) oznacza długość łańcucha rozpoczynającego się na
oznacza długość łańcucha rozpoczynającego się na 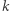 -tej pozycji. W tym rozwiązaniu będziemy wyznaczali
-tej pozycji. W tym rozwiązaniu będziemy wyznaczali ![F[k]](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/4x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif) dla kolejnych
dla kolejnych 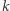 od
od  do
do 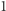 (od prawej do lewej). Załóżmy, że obliczyliśmy już
(od prawej do lewej). Załóżmy, że obliczyliśmy już ![|F[k +1],F[k + 2],...,F[n]](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/8x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif) i chcemy obliczyć
i chcemy obliczyć ![F[k].](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/9x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif) Jeśli pierwszym większym elementem na prawo od
Jeśli pierwszym większym elementem na prawo od 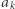 jest
jest 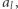 wtedy
wtedy ![F[k] = F[l]+ 1](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/12x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif) (korzystamy z wcześniej obliczonego wyniku dla l). Jeśli zaś wszystkie elementy na prawo są nie większe niż
(korzystamy z wcześniej obliczonego wyniku dla l). Jeśli zaś wszystkie elementy na prawo są nie większe niż 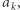 wtedy
wtedy ![F[k] = 0.](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/14x-bd354871e3ff77dad22ee83264d00b6c2d17c498-im-33,33,33-FF,FF,FF.gif)
Zastanówmy się teraz, jak dla każdego 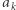 wyznaczyć pierwszy większy element na prawo od niego. Oczywiście, możemy to zrobić naiwnie (przeglądając kolejne elementy). Wówczas jednak otrzymamy rozwiązanie
wyznaczyć pierwszy większy element na prawo od niego. Oczywiście, możemy to zrobić naiwnie (przeglądając kolejne elementy). Wówczas jednak otrzymamy rozwiązanie 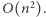
Zauważmy, że dla pary indeksów 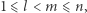 jeśli
jeśli 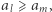 to
to 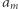 nie będzie kolejnym elementem w łańcuchu dla żadnego elementu na pozycji
nie będzie kolejnym elementem w łańcuchu dla żadnego elementu na pozycji ![|[1;l]](/math/temat/informatyka/algorytmy/2018/05/21/Ciagi_i_lancuchy/4x-1804b7c5b6d663c865e11643058838f669ef0871-im-33,33,33-FF,FF,FF.gif) (możemy myśleć o tym w ten sposób, że
(możemy myśleć o tym w ten sposób, że 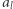 przysłania
przysłania 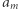 ). Zatem kandydaci na kolejny element w łańcuchu tworzą ciąg rosnący. Przeglądając ciąg
). Zatem kandydaci na kolejny element w łańcuchu tworzą ciąg rosnący. Przeglądając ciąg  od prawej do lewej, przechowujemy kandydatów na stosie. Na szczycie stosu znajduje się najmniejszy element, na dole zaś największy. Kiedy chcemy znaleźć kolejny element w łańcuchu dla
od prawej do lewej, przechowujemy kandydatów na stosie. Na szczycie stosu znajduje się najmniejszy element, na dole zaś największy. Kiedy chcemy znaleźć kolejny element w łańcuchu dla 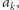 wówczas tak długo zdejmujemy elementy ze stosu, aż na szczycie stosu pojawi się element większy niż
wówczas tak długo zdejmujemy elementy ze stosu, aż na szczycie stosu pojawi się element większy niż 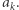 Jeśli taki element nie pojawi się, oznacza to, że taki element nie istnieje. Po wyznaczeniu kolejnego elementu w łańcuchu odkładamy
Jeśli taki element nie pojawi się, oznacza to, że taki element nie istnieje. Po wyznaczeniu kolejnego elementu w łańcuchu odkładamy 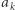 na szczyt stosu.
na szczyt stosu.
Powyższy algorytm działa w zamortyzowanym czasie liniowym. Wynika to bezpośrednio z własności stosu (każdy z 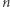 elementów został dokładnie raz odłożony na stos i raz z niego zdjęty). Powyższe rozwiązanie działa w czasie
elementów został dokładnie raz odłożony na stos i raz z niego zdjęty). Powyższe rozwiązanie działa w czasie