Informatyczny kącik olimpijski
Gotówka, Startup
Tym razem omówimy dwa zadania, które na pierwszy rzut oka wyglądają podobnie, jednak w istocie są różne. Pierwsze z nich pochodzi z II etapu IX Olimpiady Informatycznej Gimnazjalistów, zaś drugie z Bałkańskiej Olimpiady Informatycznej Juniorów w 2015 roku.
Zadanie (Gotówka). Danych jest 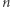 transakcji opisanych za pomocą ciągu liczb całkowitych
transakcji opisanych za pomocą ciągu liczb całkowitych 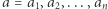 (dodatnie liczby to wpływy, zaś ujemne to wydatki). Poprawnym ciągiem transakcji nazywamy taki, podczas którego stan konta nigdy nie spadnie poniżej zera. Ile jest permutacji ciągu
(dodatnie liczby to wpływy, zaś ujemne to wydatki). Poprawnym ciągiem transakcji nazywamy taki, podczas którego stan konta nigdy nie spadnie poniżej zera. Ile jest permutacji ciągu 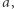 które są poprawnymi ciągami transakcji?
które są poprawnymi ciągami transakcji?
Rozwiązanie 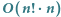 .
.
Pierwszy, najbardziej intuicyjny, pomysł polega na wygenerowaniu wszystkich 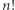 permutacji ciągu
permutacji ciągu 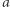 oraz zliczeniu tych, które są poprawne. Sprawdzenie, czy dana permutacja transakcji jest poprawna, możemy wykonać w czasie liniowym od jej długości. Wystarczy, że sprawdzimy, czy suma każdego prefiksu jest nieujemna. Niestety, takie podejście jest czasochłonne i działa w czasie
oraz zliczeniu tych, które są poprawne. Sprawdzenie, czy dana permutacja transakcji jest poprawna, możemy wykonać w czasie liniowym od jej długości. Wystarczy, że sprawdzimy, czy suma każdego prefiksu jest nieujemna. Niestety, takie podejście jest czasochłonne i działa w czasie 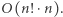
Rozwiązanie 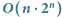 .
.
W tym rozwiązaniu wykorzystamy technikę programowania dynamicznego. Niech ![P[s] D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/2x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-im-33,33,33-FF,FF,FF.gif) oznacza liczbę poprawnych ciągów transakcji, które są permutacją ciągu
oznacza liczbę poprawnych ciągów transakcji, które są permutacją ciągu  Obliczmy wartość
Obliczmy wartość 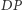 dla każdego podciągu
dla każdego podciągu 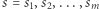 ciągu
ciągu 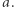 Jeśli
Jeśli  jest pusty lub suma elementów podciągu
jest pusty lub suma elementów podciągu  jest ujemna, wtedy
jest ujemna, wtedy ![P[s]=0.D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/9x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku istnieje przynajmniej jedna poprawna permutacja ciągu
W przeciwnym przypadku istnieje przynajmniej jedna poprawna permutacja ciągu  Aby obliczyć
Aby obliczyć ![P[s], D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/11x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-im-33,33,33-FF,FF,FF.gif) rozważmy
rozważmy 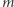 możliwości wybrania transakcji, która zostanie wykonana jako ostatnia. Liczba poprawnych ciągów transakcji, przy założeniu, że ostatnia transakcja to
możliwości wybrania transakcji, która zostanie wykonana jako ostatnia. Liczba poprawnych ciągów transakcji, przy założeniu, że ostatnia transakcja to 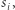 wynosi
wynosi ![P[s1,...,si−1,si+1,...,sm] |D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/14x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-im-33,33,33-FF,FF,FF.gif) (liczba poprawnych uporządkowań
(liczba poprawnych uporządkowań 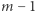 pozostałych transakcji). Zatem:
pozostałych transakcji). Zatem:
![m P[s]=QDP[s1,...,si−1,si+1,...,sm]. D i1](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/16x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-dm-33,33,33-FF,FF,FF.gif)
Liczba poprawnych permutacji dla całego ciągu to ![P[a]. D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/17x-9706a17271e21cb25f5e90e72b12a611ed3eb02a-im-33,33,33-FF,FF,FF.gif)
Ciąg  ma
ma 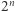 podciągów. Obliczenie
podciągów. Obliczenie ![P[s] D](/math/temat/informatyka/algorytmy/2018/04/22/Gotowka_Startup/3x-bbaca41d3bf5b5d778ad7234f39690bc8f720a23-im-33,33,33-FF,FF,FF.gif) dla
dla 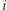 -elementowego podciągu
-elementowego podciągu  kosztuje
kosztuje 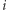 operacji, zaś
operacji, zaś 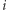 -elementowych podciągów jest
-elementowych podciągów jest 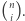 Zatem obliczenie wszystkich wartości
Zatem obliczenie wszystkich wartości 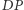 wymaga wykonania
wymaga wykonania

operacji. Rozwiązanie działa w czasie 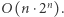
Zadanie (Startup). Dany jest ciąg 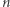 transakcji opisanych za pomocą ciągu liczb całkowitych
transakcji opisanych za pomocą ciągu liczb całkowitych 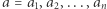 (dodatnie liczby to wpływy, zaś ujemne to wydatki). Poprawnym ciągiem transakcji nazywamy taki, podczas którego stan konta nigdy nie spadnie poniżej zera. Ile jest rotacji ciągu
(dodatnie liczby to wpływy, zaś ujemne to wydatki). Poprawnym ciągiem transakcji nazywamy taki, podczas którego stan konta nigdy nie spadnie poniżej zera. Ile jest rotacji ciągu 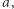 które są poprawnymi ciągami transakcji? Rotacją ciągu
które są poprawnymi ciągami transakcji? Rotacją ciągu  nazywamy
nazywamy 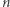 -elementowy ciąg, powstały poprzez konkatenację sufiksu i prefiksu ciągu
-elementowy ciąg, powstały poprzez konkatenację sufiksu i prefiksu ciągu  Rotacjami ciągu
Rotacjami ciągu 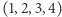 są:
są: 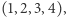
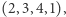
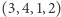 i
i 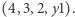
Rozwiązanie 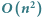 .
.
Zauważmy, że wszystkich rotacji jest 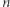 (każdy element wyznacza początek rotacji). Wystarczy zatem każdą z nich rozpatrzyć niezależnie. Sprawdzenie, czy dana rotacja jest poprawnym ciągiem transakcji, możemy wykonać w czasie liniowym od jej długości. Wystarczy sprawdzić, czy suma każdego prefiksu jest nieujemna. W ten sposób otrzymujemy rozwiązanie, które działa w czasie
(każdy element wyznacza początek rotacji). Wystarczy zatem każdą z nich rozpatrzyć niezależnie. Sprawdzenie, czy dana rotacja jest poprawnym ciągiem transakcji, możemy wykonać w czasie liniowym od jej długości. Wystarczy sprawdzić, czy suma każdego prefiksu jest nieujemna. W ten sposób otrzymujemy rozwiązanie, które działa w czasie 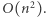
Rozwiązanie 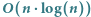 . Zastanówmy się teraz, czy możemy przyspieszyć fazę sprawdzania, czy dana rotacja jest poprawnym ciągiem transakcji - oczywiście możemy. Zacznijmy od sklejenia dwóch kopii ciągu
. Zastanówmy się teraz, czy możemy przyspieszyć fazę sprawdzania, czy dana rotacja jest poprawnym ciągiem transakcji - oczywiście możemy. Zacznijmy od sklejenia dwóch kopii ciągu  w jeden ciąg
w jeden ciąg 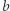 :
:

Wówczas każda rotacja jest podsłowem ciągu 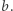
Niech 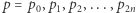 będzie ciągiem sum prefiksowych dla ciągu
będzie ciągiem sum prefiksowych dla ciągu 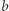 (tzn.
(tzn. 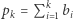 ).
).
Załóżmy, że chcemy sprawdzić poprawność rotacji 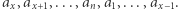 Odpowiadającym podsłowem słowa
Odpowiadającym podsłowem słowa 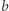 jest
jest 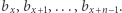 Podsłowo jest poprawnym ciągiem transakcji, jeśli każdy prefiks ma nieujemną sumę:
Podsłowo jest poprawnym ciągiem transakcji, jeśli każdy prefiks ma nieujemną sumę:

Powyższy warunek możemy równoważnie zapisać jako

oraz jako

Zauważmy, że powyższy warunek jest prawdziwy wtedy i tylko wtedy, gdy

W celu wyznaczenia minimum na przedziale możemy skorzystać ze struktury drzewa przedziałowego rozpiętego na ciągu 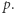 Drzewo przedziałowe pozwala w czasie
Drzewo przedziałowe pozwala w czasie 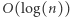 znajdować minimum na przedziale - czyli sprawdzać, czy dana rotacja jest poprawna. Wszystkich rotacji jest
znajdować minimum na przedziale - czyli sprawdzać, czy dana rotacja jest poprawna. Wszystkich rotacji jest 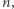 zatem rozwiązanie działa w czasie
zatem rozwiązanie działa w czasie