Informatyczny kącik olimpijski
Magic
Tym razem omówimy zadanie z pierwszego dnia Pierwszej Olimpiady Informatycznej Juniorów (EJOI), która odbyła się w Sofii we wrześniu 2017 roku.
Zadanie. Dane jest słowo 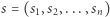 o długości
o długości 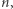 w którym występuje
w którym występuje 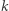 różnych liter alfabetu angielskiego. Magicznym podsłowem nazywamy niepuste podsłowo (czyli spójny fragment słowa), które zawiera taką samą liczbę wystąpień każdej z
różnych liter alfabetu angielskiego. Magicznym podsłowem nazywamy niepuste podsłowo (czyli spójny fragment słowa), które zawiera taką samą liczbę wystąpień każdej z 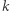 liter. Należy policzyć liczbę magicznych podsłów w słowie
liter. Należy policzyć liczbę magicznych podsłów w słowie  Podsłowa, które są takie same, ale znajdują się na różnych pozycjach, uznajemy za różne.
Podsłowa, które są takie same, ale znajdują się na różnych pozycjach, uznajemy za różne.
Na potrzeby tego artykułu przyjmijmy dodatkowe założenie, że słowo  zawiera wyłącznie litery ze zbioru
zawiera wyłącznie litery ze zbioru 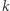 -początkowych liter alfabetu angielskiego. Aby uzyskać to założenie, wystarczy po wczytaniu słowa nadać literom nowe identyfikatory będące kolejnymi małymi literami alfabetu angielskiego.
-początkowych liter alfabetu angielskiego. Aby uzyskać to założenie, wystarczy po wczytaniu słowa nadać literom nowe identyfikatory będące kolejnymi małymi literami alfabetu angielskiego.
Rozwiązanie 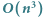 .
.
Najprostsze rozwiązanie polega na rozpatrzeniu każdego podsłowa niezależnie. Aby sprawdzić, czy dane podsłowo jest magiczne, należy zliczyć liczbę wystąpień każdej litery w podsłowie, a następnie sprawdzić, czy wszystkie otrzymane wartości są równe.
Liczba wszystkich podsłów jest rzędu 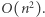 Sprawdzenie, czy podsłowo jest magiczne, wymaga
Sprawdzenie, czy podsłowo jest magiczne, wymaga 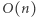 operacji. Zatem całe rozwiązanie wykonuje
operacji. Zatem całe rozwiązanie wykonuje 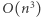 operacji.
operacji.
Rozwiązanie 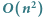 .
.
Powyższe rozwiązanie można w łatwy sposób przyspieszyć. Każdą z możliwych początkowych pozycji 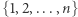 podsłowa słowa
podsłowa słowa  rozpatrzymy niezależnie. Załóżmy, że rozpatrujemy początkową pozycję
rozpatrzymy niezależnie. Załóżmy, że rozpatrujemy początkową pozycję  Przeiterujemy wszystkie potencjalne końce podsłów zaczynających się na tej pozycji. Niech
Przeiterujemy wszystkie potencjalne końce podsłów zaczynających się na tej pozycji. Niech 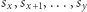 będzie aktualnie rozpatrywanym podsłowem. Zauważmy, że aby policzyć liczbę wystąpień poszczególnych liter w tym podsłowie, wystarczy skorzystać z wyniku dla podsłowa
będzie aktualnie rozpatrywanym podsłowem. Zauważmy, że aby policzyć liczbę wystąpień poszczególnych liter w tym podsłowie, wystarczy skorzystać z wyniku dla podsłowa 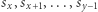 oraz zaktualizować go o wystąpienie litery
oraz zaktualizować go o wystąpienie litery 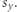 Zatem, dla ustalonego podsłowa potrafimy wyznaczyć te wartości w stałej liczbie operacji
Zatem, dla ustalonego podsłowa potrafimy wyznaczyć te wartości w stałej liczbie operacji 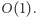 Natomiast sprawdzenie, czy dane podsłowo jest magiczne, wymaga
Natomiast sprawdzenie, czy dane podsłowo jest magiczne, wymaga 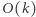 operacji (należy sprawdzić, czy liczba wystąpień każdej z
operacji (należy sprawdzić, czy liczba wystąpień każdej z 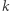 liter jest taka sama). Zauważmy, że słowa, których długość nie jest podzielna przez
liter jest taka sama). Zauważmy, że słowa, których długość nie jest podzielna przez 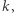 na pewno nie są magiczne. Zatem dla tych słów możemy pominąć fazę sprawdzania liczności poszczególnych liter. Słów, dla których wykonamy fazę sprawdzania liczności liter, jest
na pewno nie są magiczne. Zatem dla tych słów możemy pominąć fazę sprawdzania liczności poszczególnych liter. Słów, dla których wykonamy fazę sprawdzania liczności liter, jest 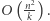 Sumarycznie wykonamy
Sumarycznie wykonamy 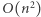 operacji.
operacji.
Przypadek dla 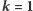
Przypadek dla 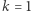 jest trywialny. Każde podsłowo jest magiczne, zatem wynikiem jest
jest trywialny. Każde podsłowo jest magiczne, zatem wynikiem jest 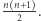
Przypadek dla 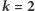
Najpierw słowo  zamieńmy na ciąg liczb
zamieńmy na ciąg liczb 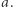 Pierwszą literę słowa oraz wszystkie jej wystąpienia zamieńmy na
Pierwszą literę słowa oraz wszystkie jej wystąpienia zamieńmy na 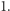 Pozostałe litery zamieńmy na
Pozostałe litery zamieńmy na 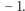 Zauważmy teraz, że każde magiczne podsłowo ma sumę
Zauważmy teraz, że każde magiczne podsłowo ma sumę 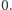
Policzmy sumy prefiksowe 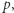 gdzie
gdzie 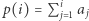 dla
dla 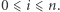 Zauważmy, że podsłowo
Zauważmy, że podsłowo 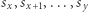 jest magiczne, jeśli
jest magiczne, jeśli 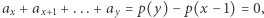 czyli jeśli
czyli jeśli 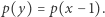 Wystarczy zatem policzyć liczbę par indeksów, dla których sumy prefiksowe są równe. W tym celu zliczmy wystąpienia elementów w ciągu
Wystarczy zatem policzyć liczbę par indeksów, dla których sumy prefiksowe są równe. W tym celu zliczmy wystąpienia elementów w ciągu 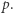 Niech
Niech 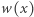 oznacza liczbę wystąpień
oznacza liczbę wystąpień 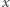 w ciągu
w ciągu 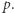 Wówczas wynikiem jest
Wówczas wynikiem jest 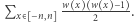 Rozwiązanie wykonuje
Rozwiązanie wykonuje 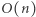 operacji.
operacji.
Rozwiązanie 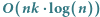 .
.
Zacznijmy od przypisania każdej literze jej unikalnego identyfikatora ze zbioru 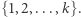 Następnie przekształćmy słowo
Następnie przekształćmy słowo  na ciąg liczb
na ciąg liczb 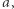 zamieniając każdą literę na odpowiadający jej identyfikator. Np. słowo kajak możemy zamienić na ciąg
zamieniając każdą literę na odpowiadający jej identyfikator. Np. słowo kajak możemy zamienić na ciąg 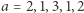 (a otrzymało identyfikator
(a otrzymało identyfikator 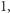 k otrzymało identyfikator
k otrzymało identyfikator 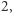 zaś j otrzymało identyfikator
zaś j otrzymało identyfikator 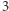 ). Od teraz będziemy operowali na ciągu liczb naturalnych.
). Od teraz będziemy operowali na ciągu liczb naturalnych.
Niech:
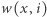 będzie równe
będzie równe 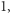 jeśli na
jeśli na 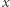 -tej pozycji występuje wartość
-tej pozycji występuje wartość 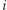 oraz 0 w przeciwnym przypadku;
oraz 0 w przeciwnym przypadku;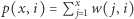 (liczba wystąpień wartości
(liczba wystąpień wartości 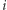 na
na 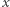 -elementowym prefiksie ciągu
-elementowym prefiksie ciągu 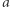 );
);![v(x) = [p(x,1),p(x, 2),...,p(x, k)]](/math/temat/informatyka/algorytmy/2018/03/25/Magic/12x-5d60be1ec8eb2e2baf5247a652ef72e6f1f43127-im-33,33,33-FF,FF,FF.gif) ; (wektor reprezentuje liczbę wystąpień poszczególnych liter na
; (wektor reprezentuje liczbę wystąpień poszczególnych liter na 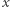 -elementowym prefiksie ciągu
-elementowym prefiksie ciągu  );
);![v′(x) = v(x)− [p(x, 1),p(x, 1),...,p(x, 1)].](/math/temat/informatyka/algorytmy/2018/03/25/Magic/16x-5d60be1ec8eb2e2baf5247a652ef72e6f1f43127-im-33,33,33-FF,FF,FF.gif)
Podsłowo 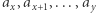 jest magiczne, jeśli:
jest magiczne, jeśli:
![v(y)− v(x − 1) = [c,c,...,c]](/math/temat/informatyka/algorytmy/2018/03/25/Magic/2x-ba0d8134b249c245d464a687317cd59d8653da2f-dm-33,33,33-FF,FF,FF.gif)
dla pewnego 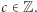 Po przekształceniach, które pozostawiam Czytelnikowi jako ćwiczenie, otrzymujemy równoważną definicję magicznego podsłowa:
Po przekształceniach, które pozostawiam Czytelnikowi jako ćwiczenie, otrzymujemy równoważną definicję magicznego podsłowa:
![′ ′ v (y)− v (x −1) = [0,0,...,0]](/math/temat/informatyka/algorytmy/2018/03/25/Magic/4x-ba0d8134b249c245d464a687317cd59d8653da2f-dm-33,33,33-FF,FF,FF.gif)
Zatem każda taka para 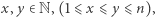 że
że ![|v′ (y) − v′ (x − 1) = [0,0,...,0]](/math/temat/informatyka/algorytmy/2018/03/25/Magic/6x-ba0d8134b249c245d464a687317cd59d8653da2f-im-33,33,33-FF,FF,FF.gif) oznacza magiczne podsłowo. Policzmy zatem, ile jest par takich samych wektorów w ciągu
oznacza magiczne podsłowo. Policzmy zatem, ile jest par takich samych wektorów w ciągu 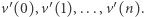 W tym celu posortujmy ten ciąg leksykograficznie. Wówczas wektory, które są równe, będą tworzyły spójny blok. Spośród bloku
W tym celu posortujmy ten ciąg leksykograficznie. Wówczas wektory, które są równe, będą tworzyły spójny blok. Spośród bloku 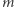 takich samych wektorów można wybrać
takich samych wektorów można wybrać 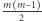 par.
par.
Obliczenie wektorów 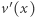 dla każdego
dla każdego 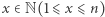 wymaga
wymaga 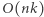 operacji, zaś sortowanie
operacji, zaś sortowanie 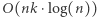 operacji. Zatem całe rozwiązania wykonuje
operacji. Zatem całe rozwiązania wykonuje 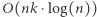 operacji.
operacji.