Bartek jest starszy od Agatki. Chodzi do prestiżowego liceum w stolicy i startuje w różnych konkursach programistycznych. Rodzice są bardzo dumni z Bartka i na ostatnie urodziny kupili mu wyjątkowo drogi komputer do nauki. Komputer ten ma procesor, pamięć RAM i wszystkie inne bajery, jakie tylko można sobie wyobrazić.

Agatka jest bardzo zapatrzona w brata. Chce być taka jak on. Od Bartka dostała jego stary komputer. Wprawdzie klawiatura jest brudna, komputer jest bardzo przestarzały i często się zawiesza, jednak nie powstrzymuje to Agatki przed nauką programowania.

Ostatnio Agatka znalazła w bibliotece książkę dotyczącą podstaw algorytmiki. Pierwszy rozdział książki był poświęcony złożoności obliczeniowej. Autorzy książki tłumaczyli, że są dwie metody sprawdzania, który algorytm działa szybciej. Pierwsza z nich to metoda empiryczna. Polega ona na napisaniu dwóch programów, uruchomieniu ich na danych testowych i zmierzeniu czasu każdego z nich. Metoda ta ma wiele wad. Różne wyniki można otrzymać w zależności od tego, na jakim komputerze uruchomimy program, jaka będzie architektura procesora, jaka będzie struktura pamięci komputera, jakich kompilatorów użyjemy, w jakich językach napiszemy programy, jaki będzie rozmiar danych testowych, jakie dane testowe użyjemy czy jakie liczby wygeneruje generator liczb losowych. Mówiąc prościej - wynik eksperymentu może zależeć od wielu czynników. Przede wszystkim jednak wadą tej metody jest to, że najpierw należy oba programy napisać na komputerze - co w przypadku skomplikowanych algorytmów może okazać się czasochłonne.

Drugą metodę autorzy tłumaczą na przykładzie poniższego programu:

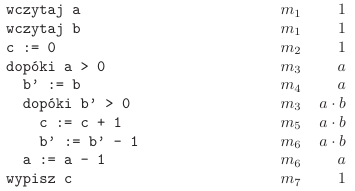
Jeśli chcielibyśmy ustalić, ile czasu zajmie komputerowi obliczenie powyższego programu, musielibyśmy wiedzieć, ile milisekund zajmuje mu wykonanie każdej z instrukcji. Ponieważ to zależy od komputera (a jak napisali autorzy książki: "my chcemy zajmować się algorytmami, a nie maszynami liczącymi"), ustalimy sobie pewne stałe. Założymy, że instrukcja wczytaj a wykona się na komputerze w milisekund, instrukcja c := 0 wykona się w 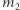milisekundy, i tak dalej. Następnie chcemy policzyć, ile razy (w najgorszym przypadku) wykonywana będzie dana instrukcja przez komputer. Dla przykładu: instrukcja wczytaj a wykona się 1 raz, natomiast instrukcja c := c + 1 wykona się 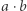razy. Można obliczyć, że program będzie wykonywać się przez następującą liczbę milisekund:

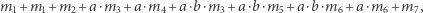co można zapisać krócej jako:

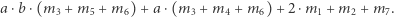Teraz będziemy się zastanawiać, co się będzie działo, gdy wartości 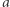oraz 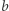będą bardzo duże. Można zauważyć wtedy, że pierwszy i drugi składnik będą tak dużo większe od trzeciego, że trzeci będzie w porównaniu z nimi pomijalnie mały. Pomińmy go zatem:

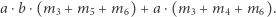Teraz spróbujemy sobie wyobrazić, co się stanie, gdy wartości 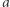oraz 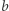będą naprawdę bardzo, bardzo duże. Wtedy pierwszy składnik sumy będzie na tyle duży, że wartość drugiego składnika stanie się w porównaniu z nim pomijalnie mała. Zatem i ją pomińmy:

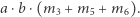Ponieważ, jak wielokrotnie autorzy książki już wspominali, chcemy zajmować się algorytmami, a nie komputerami - pomińmy dodatkowo współczynnik w nawiasie:

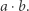Otrzymaliśmy coś, co informatycy nazywają asymptotyczną złożonością obliczeniową algorytmu. Mówi się czasem, że algorytm działa w czasie 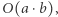albo że algorytm ma złożoność 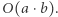Metoda ta ma dwie podstawowe zalety. Po pierwsze - bardzo łatwo ją zastosować. Tak naprawdę nie potrzebujemy nawet powtarzać wszystkich tych kroków, które poczyniliśmy. Wystarczy, że spojrzymy na algorytm i zastanowimy się, która instrukcja będzie wykonywana najczęściej przez program. W naszym przykładzie jest to linijka c := c + 1 i faktycznie jest ona wykonywana dokładnie 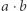razy. Po drugie, łatwo na podstawie złożoności określić, który algorytm będzie działał szybciej. I to jeszcze przed napisaniem go na komputerze! Dla przykładu: algorytm działający w czasie 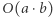działa wolniej od algorytmu 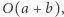a ten z kolei od algorytmu ze złożonością 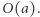Oczywiście, metoda ta ma również wady. Po pierwsze, mówi ona, co się dzieje dla dużych danych. O tym, który algorytm działa szybciej dla małych danych, nie mówi nic. Po drugie, jeśli dwa algorytmy mają taką samą złożoność - nie dowiemy się, który działa krócej.

Uzbrojona w nową wiedzę Agatka postanowiła wyzwać swojego brata na pojedynek. Założyła się z bratem, że jej program sortujący zadziała na jej wolnym komputerze szybciej niż program sortujący Bartka na jego superkomputerze. Bartek bez zastanowienia przyjął zakład. Napisanie programu zajęło mu 5 minut. Agatce natomiast zajęło to cały dzień. Bartek nie wiedział jednak, że Agatka wie, że Bartek zna tylko jeden algorytm sortowania. W książce przeczytała też, że złożoność tego algorytmu to 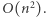W rozdziale dalej z kolei był podany algorytm sortowania o złożoności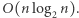

Kto wyjdzie z tego pojedynku zwycięsko? Bartek jest świetnym programistą. Stała ukryta w złożoności programu Bartka wynosi 1/10. Ponadto Bartek tak zaprogramował swój algorytm, że jest on w stanie pracować równolegle na wszystkich czterech rdzeniach jego komputera bez żadnych dodatkowych narzutów czasowych. Każdy z rdzeni jego komputera taktuje z częstotliwością 2,5 GHz. Agatka nie jest jeszcze taką dobrą programistką jak jej starszy brat. Stała ukryta w złożoności programu Agatki wynosi 20. Komputer Agatki to bardzo stary Commodore 64 z procesorem taktującym z częstotliwością 1 MHz. Wydawać by się mogło, że Agatka nie ma żadnych szans. Jednak sprytna siostra zażądała, żeby sortowali oboje wszystkich ludzi na świecie. W sumie około 8000000000 nazwisk.

Komputery będą działały długo i trochę wody w Wiśle upłynie, zanim rodzeństwo dowie się, kto wygrał zakład. My to obliczymy już teraz. Przyjmując dodatkowe założenia, możemy obliczyć, że program Agaty będzie się liczył około 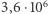sekund, natomiast program Bartka 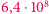sekund. Mówiąc bardziej obrazowo: program Agatki skończy się liczyć w półtora miesiąca, natomiast program Bartka będzie się liczył ponad 20 lat.