Kieszonkowe
Dzisiejsze zadanie pochodzi z VIII. Olimpiady Informatycznej Gimnazjalistów w roku szkolnym 2013/2014.
Zadanie. Danych jest  stosów, ponumerowanych od
stosów, ponumerowanych od 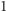 do
do 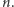 Każdy stos zawiera dokładnie dwie monety, ułożone jedna na drugiej. Ciąg
Każdy stos zawiera dokładnie dwie monety, ułożone jedna na drugiej. Ciąg 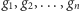 oznacza nominały monet, znajdujących się na górze kolejnych stosów, zaś ciąg
oznacza nominały monet, znajdujących się na górze kolejnych stosów, zaś ciąg 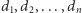 nominały monet, znajdujących się na dole kolejnych stosów. Staś, bohater zadania, może wykonać co najwyżej
nominały monet, znajdujących się na dole kolejnych stosów. Staś, bohater zadania, może wykonać co najwyżej 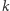 ruchów. W każdym ruchu chłopiec wybiera dowolny niepusty stos i zabiera monetę ze szczytu tego stosu. Jaki jest największy możliwy zysk Stasia?
ruchów. W każdym ruchu chłopiec wybiera dowolny niepusty stos i zabiera monetę ze szczytu tego stosu. Jaki jest największy możliwy zysk Stasia?
Rozwiązanie dynamiczne. Zadanie możemy rozwiązać, korzystając z metody programowania dynamicznego. Niech ![P[i][ j] D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/1x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) oznacza maksymalny zysk dla problemu ograniczonego do stosów o numerach od
oznacza maksymalny zysk dla problemu ograniczonego do stosów o numerach od 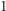 do
do 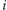 oraz maksymalnej liczbie ruchów równej
oraz maksymalnej liczbie ruchów równej 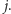 Łatwo obliczyć wartości
Łatwo obliczyć wartości 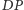 dla pierwszego stosu
dla pierwszego stosu 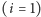 :
:
![P[1][0]=0 D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/8x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) ;
;![P[1][1]=g D 1](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/10x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) ;
;![P[1][ j]=g1+d1, D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/12x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) dla
dla 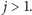
Przejdźmy teraz do obliczenia wyników dla większej liczby stosów. Dla każdego 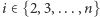 oraz
oraz 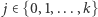 aby obliczyć wartość
aby obliczyć wartość ![P[i][ j],D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/16x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) należy rozpatrzyć trzy sytuacje:
należy rozpatrzyć trzy sytuacje:
- nie bierzemy ani jednej monety z
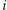 -tego stosu, wtedy wynikiem jest
-tego stosu, wtedy wynikiem jest ![P[i−1][ j] D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/19x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) ;
; - bierzemy jedną monetę z
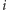 -tego stosu, wtedy wynikiem jest
-tego stosu, wtedy wynikiem jest ![P[i−1][ j−1]+gi D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/22x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) ;
; - bierzemy dwie monety z
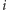 -tego stosu, wtedy wynikiem jest
-tego stosu, wtedy wynikiem jest ![P[i−1][ j−2]+g+d. D ii](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/25x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif)
Wartością ![P[i][ j] D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/26x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif) jest maksimum z trzech powyższych wartości. Oczywiście, druga sytuacja jest możliwa tylko dla
jest maksimum z trzech powyższych wartości. Oczywiście, druga sytuacja jest możliwa tylko dla 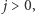 podobnie trzecia tylko dla
podobnie trzecia tylko dla 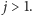 Największym zyskiem Stasia jest
Największym zyskiem Stasia jest ![P[n][k]. D](/math/temat/informatyka/algorytmy/2018/02/26/Kieszonkowe/29x-6579335cf83983326475aa1260defd20b0b51f46-im-33,33,33-FF,FF,FF.gif)
Wszystkich stanów jest 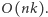 Obliczenie wyniku dla każdego stanu odbywa się w czasie stałym. Stąd złożoność czasowa rozwiązania wynosi
Obliczenie wyniku dla każdego stanu odbywa się w czasie stałym. Stąd złożoność czasowa rozwiązania wynosi 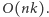
Rozwiązanie zachłanne. Okazuje się, że istnieje rozwiązanie o lepszej złożoności czasowej. Na początku podzielmy stosy na dwie grupy. Niech pierwsza grupa zawiera stosy, których górna moneta ma nominał nie mniejszy niż dolna moneta, nazwijmy je 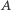 -stosami. Pozostałe stosy niech tworzą drugą grupę i nazwijmy je
-stosami. Pozostałe stosy niech tworzą drugą grupę i nazwijmy je 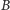 -stosami. Każdą z tych grup rozważmy oddzielnie.
-stosami. Każdą z tych grup rozważmy oddzielnie.
Przypadek 1: 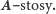 Załóżmy, że mamy
Załóżmy, że mamy 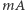 -stosów. Chcemy wybrać
-stosów. Chcemy wybrać  monet, których sumaryczna wartość jest największa. Załóżmy dodatkowo, że w każdym ruchu możemy wybrać dowolną monetę (górną lub dolną). Nietrudno zauważyć, że aby zmaksymalizować zysk, należy wybrać
monet, których sumaryczna wartość jest największa. Załóżmy dodatkowo, że w każdym ruchu możemy wybrać dowolną monetę (górną lub dolną). Nietrudno zauważyć, że aby zmaksymalizować zysk, należy wybrać 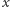 monet o największym nominale. Zatem posortujmy wszystkie monety malejąco według nominału. Otrzymujemy ciąg
monet o największym nominale. Zatem posortujmy wszystkie monety malejąco według nominału. Otrzymujemy ciąg 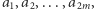 oznaczający wartości wszystkich monet. Największy zysk uzyskamy, jeśli weźmiemy następujące monety:
oznaczający wartości wszystkich monet. Największy zysk uzyskamy, jeśli weźmiemy następujące monety: 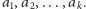
Strategia zachłanna, która została opisana powyżej, jest również poprawna bez dodatkowego założenia o braniu dowolnej monety. Ustalamy zatem, że możemy brać tylko monety ze szczytu stosu. Przypuśćmy, że w optymalnym rozwiązaniu chcemy wziąć dwie monety 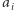 (górną) i
(górną) i 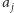 (dolną), które tworzą jeden stos. Skoro rozważamy
(dolną), które tworzą jeden stos. Skoro rozważamy 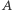 -stos
-stos 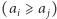 oraz ciąg
oraz ciąg  jest posortowany malejąco, to
jest posortowany malejąco, to 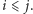 Zatem strategia zachłanna jest poprawna, ponieważ najpierw wybierze górną monetę
Zatem strategia zachłanna jest poprawna, ponieważ najpierw wybierze górną monetę 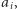 a dopiero potem dolną
a dopiero potem dolną 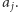 Tutaj jest drobna subtelność, jeśli dwie monety mają ten sam nominał, wtedy pierwszeństwo ma górna.
Tutaj jest drobna subtelność, jeśli dwie monety mają ten sam nominał, wtedy pierwszeństwo ma górna.
Przypadek 2: 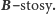 Załóżmy, że mamy
Załóżmy, że mamy 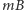 -stosów. Chcemy wybrać
-stosów. Chcemy wybrać 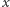 monet, których sumaryczna wartość jest największa. Przypuśćmy, że w optymalnym rozwiązaniu istnieją dwa stosy (o numerach
monet, których sumaryczna wartość jest największa. Przypuśćmy, że w optymalnym rozwiązaniu istnieją dwa stosy (o numerach 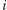 oraz
oraz 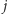 ), z których zabieramy po jednej monecie. Bez straty ogólności możemy założyć, że
), z których zabieramy po jednej monecie. Bez straty ogólności możemy założyć, że 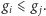 Wiadomo (z własności
Wiadomo (z własności 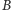 -stosu), że
-stosu), że 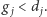 Skoro
Skoro 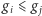 oraz
oraz 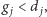 to
to 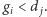 Zatem wzięcie po jednej monecie ze stosów
Zatem wzięcie po jednej monecie ze stosów 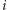 i
i 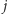 nie jest optymalnym rozwiązaniem, gdyż bardziej opłaca się wziąć dwie monety z
nie jest optymalnym rozwiązaniem, gdyż bardziej opłaca się wziąć dwie monety z 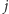 -tego stosu. Stąd otrzymujemy, że w optymalnym rozwiązaniu nie ma dwóch stosów, z których zabieramy po jednej monecie. Innymi słowy, jest co najwyżej jeden stos, z którego zabieramy jedną monetę.
-tego stosu. Stąd otrzymujemy, że w optymalnym rozwiązaniu nie ma dwóch stosów, z których zabieramy po jednej monecie. Innymi słowy, jest co najwyżej jeden stos, z którego zabieramy jedną monetę.
Zatem posortujmy stosy według malejącej sumy nominałów. Otrzymujemy ciąg 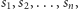 gdzie
gdzie 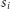 oznacza sumę nominałów
oznacza sumę nominałów 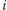 -tego najcenniejszego stosu. Jeśli
-tego najcenniejszego stosu. Jeśli 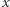 jest parzyste, to wybieramy monety ze stosów
jest parzyste, to wybieramy monety ze stosów 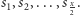 W przeciwnym przypadku rozważamy dwie sytuacje. Pierwsza z nich polega na wzięciu stosów
W przeciwnym przypadku rozważamy dwie sytuacje. Pierwsza z nich polega na wzięciu stosów 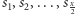 oraz monety o największym nominale spośród szczytów pozostałych stosów. Druga zaś polega na wzięciu stosów
oraz monety o największym nominale spośród szczytów pozostałych stosów. Druga zaś polega na wzięciu stosów 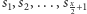 bez monety o najmniejszym nominale spośród spodów wybranych stosów.
bez monety o najmniejszym nominale spośród spodów wybranych stosów.
Podsumowanie. Rozwiązanie opiera się na rozpatrzeniu dla każdego 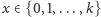 następującego przypadku: wybieramy
następującego przypadku: wybieramy 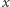 monet z
monet z 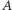 -stosów oraz
-stosów oraz  monet z
monet z 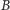 -stosów. Wynikiem jest maksimum spośród wyników dla tych przypadków. Całe rozwiązanie działa w czasie
-stosów. Wynikiem jest maksimum spośród wyników dla tych przypadków. Całe rozwiązanie działa w czasie 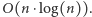 Szczegóły implementacyjne pozostawiam Czytelnikowi jako ćwiczenie.
Szczegóły implementacyjne pozostawiam Czytelnikowi jako ćwiczenie.