Informatyczny kącik olimpijski
Ciąg arytmetyczny i Kamyczki
Tym razem omówimy dwa zadania z jubileuszowej X Olimpiady Informatycznej Gimnazjalistów w roku szkolnym 2015/2016.
Zadanie (Ciąg arytmetyczny). Dany jest ciąg 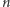 liczb naturalnych
liczb naturalnych 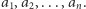 Naszym zadaniem jest odpowiedzieć na
Naszym zadaniem jest odpowiedzieć na 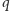 zapytań postaci: czy podsłowo
zapytań postaci: czy podsłowo 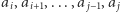 jest ciągiem arytmetycznym?
jest ciągiem arytmetycznym?
Zacznijmy od przypomnienia definicji ciągu arytmetycznego. Otóż, 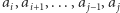 jest ciągiem arytmetycznym, jeśli różnice między kolejnymi parami wyrazów są równe, czyli:
jest ciągiem arytmetycznym, jeśli różnice między kolejnymi parami wyrazów są równe, czyli:

Rozwiązanie ( 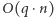 ). Najprostsze rozwiązanie polega na sprawdzeniu dla każdego zapytania, wprost z definicji, czy dany ciąg jest arytmetyczny. W tym celu wyznaczamy różnicę ciągu jako
). Najprostsze rozwiązanie polega na sprawdzeniu dla każdego zapytania, wprost z definicji, czy dany ciąg jest arytmetyczny. W tym celu wyznaczamy różnicę ciągu jako 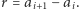 Następnie sprawdzamy, czy różnica między każdymi dwoma sąsiednimi wyrazami jest równa
Następnie sprawdzamy, czy różnica między każdymi dwoma sąsiednimi wyrazami jest równa 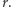 Powyższe rozwiązanie działa w czasie
Powyższe rozwiązanie działa w czasie 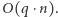
Rozwiązanie ( 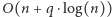 ). Niech
). Niech  będzie ciągiem różnic między kolejnymi wyrazami:
będzie ciągiem różnic między kolejnymi wyrazami:

Ciąg 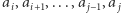 jest arytmetyczny, jeśli odpowiadający mu ciąg różnic
jest arytmetyczny, jeśli odpowiadający mu ciąg różnic 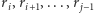 jest stały (wszystkie wyrazy są równe). Niech zatem
jest stały (wszystkie wyrazy są równe). Niech zatem 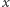 będzie najmniejszą liczbą w ciągu, zaś
będzie najmniejszą liczbą w ciągu, zaś 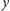 największą. Wówczas wszystkie różnice znajdują się w przedziale
największą. Wówczas wszystkie różnice znajdują się w przedziale ![|[x; y].](/math/temat/informatyka/algorytmy/2018/01/25/Ciag_arytmetyczny_i_Kamyczki/8x-ba08ad3ffc44c4de33c464738dd1c831cc63dfa1-im-33,33,33-FF,FF,FF.gif) Stąd, jeśli
Stąd, jeśli 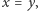 to ciąg różnic jest stały, czyli pierwotny ciąg jest arytmetyczny. Do wyznaczenia najmniejszego i największego elementu w przedziale można wykorzystać drzewo przedziałowe, które pozwala zrealizować tę operację w czasie
to ciąg różnic jest stały, czyli pierwotny ciąg jest arytmetyczny. Do wyznaczenia najmniejszego i największego elementu w przedziale można wykorzystać drzewo przedziałowe, które pozwala zrealizować tę operację w czasie 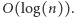 Całe rozwiązanie działa w czasie
Całe rozwiązanie działa w czasie 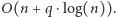
Rozwiązanie ( 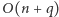 ). Okazuje się, że istnieje jeszcze szybsze rozwiązanie. Zauważmy, że ciąg różnic możemy podzielić na fragmenty o tych samych wartościach:
). Okazuje się, że istnieje jeszcze szybsze rozwiązanie. Zauważmy, że ciąg różnic możemy podzielić na fragmenty o tych samych wartościach:

Wówczas fragment 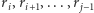 jest stały, jeśli wszystkie jego wyrazy należą do jednej grupy. Przejdźmy teraz do opisu generowania grup. Ustalmy, że pierwsza różnica tworzy pierwszą grupę. Pozostałe różnice będziemy przeglądali od lewej do prawej. Jeśli rozpatrywana różnica jest równa poprzedniej, to rozszerzamy poprzednią grupę, w przeciwnym przypadku tworzymy nową grupę. Rozwiązanie działa w czasie
jest stały, jeśli wszystkie jego wyrazy należą do jednej grupy. Przejdźmy teraz do opisu generowania grup. Ustalmy, że pierwsza różnica tworzy pierwszą grupę. Pozostałe różnice będziemy przeglądali od lewej do prawej. Jeśli rozpatrywana różnica jest równa poprzedniej, to rozszerzamy poprzednią grupę, w przeciwnym przypadku tworzymy nową grupę. Rozwiązanie działa w czasie 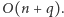
Zadanie (Kamyczki). Danych jest  stosów kamyczków. Wysokości kolejnych stosów to
stosów kamyczków. Wysokości kolejnych stosów to 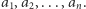 Celem Małgosi, bohaterki zadania, jest opróżnienie wszystkich stosów. Dziewczyna w jednym ruchu może opróżnić jeden dowolnie wybrany stos (nazwijmy ten ruch A) lub zabrać po jednym kamieniu z wszystkich niepustych stosów (nazwijmy ten ruch B). Ile minimalnie ruchów musi wykonać dziewczynka, aby opróżnić wszystkie stosy?
Celem Małgosi, bohaterki zadania, jest opróżnienie wszystkich stosów. Dziewczyna w jednym ruchu może opróżnić jeden dowolnie wybrany stos (nazwijmy ten ruch A) lub zabrać po jednym kamieniu z wszystkich niepustych stosów (nazwijmy ten ruch B). Ile minimalnie ruchów musi wykonać dziewczynka, aby opróżnić wszystkie stosy?
Obserwacja. Istnieje optymalne rozwiązanie, w którym najpierw wykonujemy ruchy typu A, a następnie ruchy typu B.
Dowód. Weźmy dowolne optymalne rozwiązanie. Jeśli w tym rozwiązaniu istnieje taki ruch  typu A, który występuje po jakimś ruchu typu B, to ruch
typu A, który występuje po jakimś ruchu typu B, to ruch  nie ma wpływu na pozostałe stosy oraz wcześniejsze ruchy typu B nie są konieczne do wykonania ruchu
nie ma wpływu na pozostałe stosy oraz wcześniejsze ruchy typu B nie są konieczne do wykonania ruchu 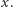 Stąd ruch
Stąd ruch  może zostać wykonany przed wszystkimi ruchami typu B.
może zostać wykonany przed wszystkimi ruchami typu B.
Na mocy powyższej obserwacji w optymalnym rozwiązaniu najpierw wykonujemy ruchy typu A, a następnie ruchy typu B. Zauważmy, że maksymalna liczba ruchów typu A to  (jest co najwyżej
(jest co najwyżej 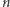 stosów do opróżnienia). Dla każdej możliwej liczby ruchów A (od 0 do
stosów do opróżnienia). Dla każdej możliwej liczby ruchów A (od 0 do 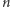 ) obliczmy minimalną liczbę ruchów B, która pozwoli opróżnić wszystkie stosy.
) obliczmy minimalną liczbę ruchów B, która pozwoli opróżnić wszystkie stosy.
Zastanówmy się teraz, jak dla ustalonej liczby 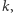 oznaczającej liczbę ruchów A, wybrać
oznaczającej liczbę ruchów A, wybrać 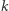 stosów do usunięcia tak, aby zminimalizować liczbę ruchów B. Zauważmy wcześniej, że po wykonaniu
stosów do usunięcia tak, aby zminimalizować liczbę ruchów B. Zauważmy wcześniej, że po wykonaniu 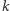 ruchów typu A należy wykonać tyle ruchów B, ile wynosi wysokość najwyższego z pozostałych stosów. Stąd, aby zminimalizować liczbę ruchów typu B, należy wybrać
ruchów typu A należy wykonać tyle ruchów B, ile wynosi wysokość najwyższego z pozostałych stosów. Stąd, aby zminimalizować liczbę ruchów typu B, należy wybrać 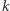 najwyższych stosów, co minimalizuje wysokość najwyższego z pozostałych stosów.
najwyższych stosów, co minimalizuje wysokość najwyższego z pozostałych stosów.
Przejdźmy teraz do opisu sposobu znajdowania 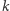 najwyższych stosów. Kolejność stosów nie ma znaczenia, dlatego zacznijmy od posortowania ciągu
najwyższych stosów. Kolejność stosów nie ma znaczenia, dlatego zacznijmy od posortowania ciągu 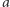 rosnąco oraz ustalenia, że
rosnąco oraz ustalenia, że 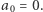 Wówczas
Wówczas 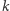 najwyższych stosów to:
najwyższych stosów to: 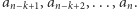 Zatem wynik dla ustalonego
Zatem wynik dla ustalonego 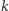 to
to 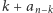 (wykonujemy
(wykonujemy 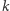 ruchów typu A, usuwając
ruchów typu A, usuwając 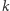 najwyższych stosów, oraz
najwyższych stosów, oraz 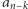 ruchów typu B, opróżniając wszystkie pozostałe stosy, z których najwyższy ma wysokość
ruchów typu B, opróżniając wszystkie pozostałe stosy, z których najwyższy ma wysokość 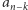 ).
).
Najmniejszą liczbą ruchów, potrzebną do opróżnienia wszystkich stosów, jest minimum z wyników dla każdego 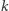 od 0 do
od 0 do 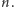 Rozwiązanie działa w czasie
Rozwiązanie działa w czasie