Kwantowe wyżarzanie „klasycznej” optymalizacji
Wydaje się, że moc, szybkość obliczeniowa współczesnych komputerów, bazujących na krzemie, osiąga swoje plateau wynikłe z ograniczeń natury materiałowej. Jednocześnie w wielu dziedzinach życia codziennego, poczynając od prób unikania korków w planowanej podróży, poprzez minimalizację kosztochłonności produkcji aż po liczne zaawansowane zagadnienia badawcze z zakresu teorii sterowania, staramy się optymalizować nasze postępowanie. Wobec wspomnianych ograniczeń sprzętowych pozostaje nam poszukiwanie nowych algorytmów dla optymalizacji lub zupełnie nowych paradygmatów obliczeniowych - być może kwantowych?

Komputer D-Wave, opisywany w tym artykule, nie realizuje standardowego modelu obliczeń kwantowych opisanego w artykule O modelach obliczeń komputerowych. Realizuje tak zwany model adiabatycznych obliczeń kwantowych, który - choć jest koncepcyjnie zupełnie inny - to jest (wielomianowo) równoważny obliczeniowo modelowi standardowemu.
Jak się okazuje, istnieje wcale niemała grupa zagadnień, które można wyrazić w języku fizyki poprzez przetłumaczenie ich, odwzorowanie na stary problem poszukiwania minimalizującej energię konfiguracji szkła spinowego w starym i powszechnie szanowanym modelu Isinga. Informatykowi wystarczy wiedzieć, że rzecz tyczy problemu znalezienia globalnego minimum, najmniejszej wartości funkcji wielu zmiennych o argumentach binarnych. Tak naprawdę funkcja ta opisuje energię układu, a zmienne binarne to wartości spinu w węzłach pewnej sieci. W związku z tym, że problem poszukiwania konfiguracji szkła jest NP-trudny, to poszukiwanie nowych metod jego rozwiązywania jest bardzo ciekawe i pożądane. Jednym z przykładów takich prób jest algorytm symulowanego wyżarzania, w ramach którego wcześniej "podgrzany" układ w procesie powolnego "schładzania" relaksuje do szukanej konfiguracji minimalizującej energię. Inna strategia, wiążąca się z intensywnym rozwojem nowego paradygmatu obliczeniowego, nazywanego dziś powszechnie obliczeniami kwantowymi, zaowocowała powstaniem i - co bardzo ważne - komercyjną implementacją algorytmu wyżarzania kwantowego.
Klasyczny problem optymalizacyjny: przykład
Załóżmy, że mamy dany prosty graf nieskierowany 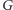 o wierzchołkach
o wierzchołkach 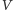 i krawędziach
i krawędziach 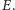 W jaki sposób wydajnie podzielić
W jaki sposób wydajnie podzielić 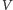 na dwa rozłączne i niepuste podzbiory tak, aby liczba krawędzi łączących wierzchołki nieznajdujące się w jednym zbiorze była możliwie największa? Mimo prostego sformułowania rozwiązanie powyższego problemu nie jest trywialne, nie jest znany ogólny algorytm pozwalający rozwiązać go w wielomianowym czasie na znanych nam z codziennej pracy klasycznych komputerach.
na dwa rozłączne i niepuste podzbiory tak, aby liczba krawędzi łączących wierzchołki nieznajdujące się w jednym zbiorze była możliwie największa? Mimo prostego sformułowania rozwiązanie powyższego problemu nie jest trywialne, nie jest znany ogólny algorytm pozwalający rozwiązać go w wielomianowym czasie na znanych nam z codziennej pracy klasycznych komputerach.
Zanim przedstawimy alternatywny sposób, w jaki współczesna fizyka pozwala nam zaatakować powyższy problem, spróbujmy znaleźć najpierw jego matematyczne sformułowanie, które ma, jak okaże się, wiele wspólnego ze znanym fizykom modelem Isinga. Ponumerujmy zatem wierzchołki naszego grafu kolejnymi liczbami naturalnymi. Wówczas podział zbioru 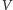 to przypisanie każdemu z wierzchołków jednej z liczb
to przypisanie każdemu z wierzchołków jednej z liczb 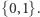 Oznaczmy liczbę przypisaną
Oznaczmy liczbę przypisaną 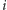 -temu wierzchołkowi przez
-temu wierzchołkowi przez 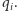 Wtedy liczba krawędzi, które łączą wierzchołki znajdujące się w różnych podzbiorach, jest dana wzorem:
Wtedy liczba krawędzi, które łączą wierzchołki znajdujące się w różnych podzbiorach, jest dana wzorem:
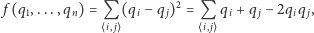 |
(1) |
gdzie sumowanie odbywa się po sąsiadujących ze sobą wierzchołkach, przy czym każdą parę takich wierzchołków zliczamy tylko raz. Rozwiązanie naszego problemu sprowadza się więc do znalezienia takiej konfiguracji 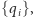 dla której wartość funkcji
dla której wartość funkcji 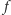 jest największa - lub równoważnie - wartość funkcji
jest największa - lub równoważnie - wartość funkcji 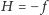 jest najmniejsza. Zauważmy, że jeśli funkcję
jest najmniejsza. Zauważmy, że jeśli funkcję 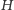 interpretujemy jako "energię" układu, otrzymujemy model typu Isinga. Funkcja
interpretujemy jako "energię" układu, otrzymujemy model typu Isinga. Funkcja 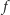 ma pewną istotną cechę - jest funkcją kwadratową zmiennych zero-jedynkowych. Problemy minimalizacyjne zadane za pomocą takich właśnie funkcji, nazywane w skrócie QUBO, stanowią klasę problemów, które możemy rozwiązać za pomocą kwantowego wyżarzania. Idea jest bardzo prosta i opiera się na przejawianej przez układy kwantowe tendencji do pozostawania w stanie o najniższej energii - stanie podstawowym - o ile ich ewolucja przebiega dostatecznie wolno, czyli adiabatycznie.
ma pewną istotną cechę - jest funkcją kwadratową zmiennych zero-jedynkowych. Problemy minimalizacyjne zadane za pomocą takich właśnie funkcji, nazywane w skrócie QUBO, stanowią klasę problemów, które możemy rozwiązać za pomocą kwantowego wyżarzania. Idea jest bardzo prosta i opiera się na przejawianej przez układy kwantowe tendencji do pozostawania w stanie o najniższej energii - stanie podstawowym - o ile ich ewolucja przebiega dostatecznie wolno, czyli adiabatycznie.
Rażąco stronnicza historia informatyki kwantowej napisana w kontekście wyżarzania
Mechanika kwantowa powstała na początku XX stulecia w dość typowy dla nauki sposób: jako teoria próbująca wyjaśnić problemy i zjawiska, z którymi ówczesna fizyka nie mogła sobie poradzić. Jako pierwszy pojęciem kwantyzacji posłużył się Max Planck, który zaproponował rewolucyjny model promieniowania ciała doskonale czarnego, w którym przyjął, że energia fal elektromagnetycznych emitowanych przez ciało doskonale czarne nie jest ciągła, ale może przyjmować jedynie wartości będące wielokrotnościami pewnej elementarnej porcji (kwantu) energii. Analogiczny pomysł został zastosowany w 1905 roku przez Einsteina, który zakładając kwantowanie energii, wyjaśnił zjawisko fotoelektryczne. Dalszy rozwój mechaniki kwantowej to efekt pracy wielu słynnych fizyków.
W mechanice klasycznej opisujemy układ, podając jego położenie i pęd, jakie ma w konkretnej chwili. W mechanice kwantowej jest inaczej: opisywany przez nas układ reprezentujemy przez tzw. wektor stanu, czyli jednostkowy wektor w pewnej, dość abstrakcyjnej, przestrzeni Hilberta. Najprostszym układem kwantowym jest spin, a jako że mówimy tu o obliczeniach kwantowych - kubit. Przestrzeń Hilberta takiego układu jest dwuwymiarowa, a jej bazę tworzą dwa bity 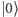 oraz
oraz 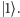 Wielkościom obserwowalnym, obserwablom takim jak energia, odpowiadają dwuwymiarowe macierze hermitowskie dane przez kombinacje liniowe macierzy jednostkowej oraz słynnych macierzy Pauliego
Wielkościom obserwowalnym, obserwablom takim jak energia, odpowiadają dwuwymiarowe macierze hermitowskie dane przez kombinacje liniowe macierzy jednostkowej oraz słynnych macierzy Pauliego 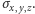 Wartości własne obserwabli to możliwe do uzyskania w drodze pomiaru wyniki.
Wartości własne obserwabli to możliwe do uzyskania w drodze pomiaru wyniki.
Przestrzeń Hilberta jest liniowa, zatem stany układu tworzą superpozycje - kombinacje liniowe wektorów bazy (bitów) 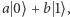 gdzie skalary
gdzie skalary 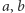 są tak dobrane, aby spełniały warunek unormowania
są tak dobrane, aby spełniały warunek unormowania 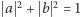 oraz, co istotne, są liczbami zespolonymi, co, jak można się domyślić, nie ułatwia ich narysowania. To właśnie zjawisko superpozycji, niemające swojego klasycznego odpowiednika, leży u podstaw informatyki kwantowej, gdyż superpozycja bitów tworzy kubit, czyli kwantową jednostkę informacji. Wśród pomysłodawców wykorzystania kwantowych zjawisk do wykonywania obliczeń wymienić można takich fizyków jak Paul Benioff, Yuri Manin, Richard Feynman czy David Deutsch. Istnieje dziś kilka modeli obliczeń kwantowych: kwantowe obwody logiczne, kwantowe maszyny Turinga czy adiabatyczne obliczenia kwantowe. Wszystkie je łączy idea wykorzystania do obliczeń kubitów w miejsce bitów klasycznych, co czyni komputer kwantowy fundamentalnie różnym od komputera klasycznego.
oraz, co istotne, są liczbami zespolonymi, co, jak można się domyślić, nie ułatwia ich narysowania. To właśnie zjawisko superpozycji, niemające swojego klasycznego odpowiednika, leży u podstaw informatyki kwantowej, gdyż superpozycja bitów tworzy kubit, czyli kwantową jednostkę informacji. Wśród pomysłodawców wykorzystania kwantowych zjawisk do wykonywania obliczeń wymienić można takich fizyków jak Paul Benioff, Yuri Manin, Richard Feynman czy David Deutsch. Istnieje dziś kilka modeli obliczeń kwantowych: kwantowe obwody logiczne, kwantowe maszyny Turinga czy adiabatyczne obliczenia kwantowe. Wszystkie je łączy idea wykorzystania do obliczeń kubitów w miejsce bitów klasycznych, co czyni komputer kwantowy fundamentalnie różnym od komputera klasycznego.
Koniec XX i początek XXI wieku to okres intensywnych prac nad teorią obliczeń kwantowych i kwantowych algorytmów, jak również nad próbami fizycznych implementacji tychże teorii. Prawdopodobnie najsłynniejszym algorytmem kwantowym jest służący do faktoryzacji dużych liczb naturalnych algorytm zaproponowany w 1994 roku przez Petera Shora. Algorytm ten doczekał się kilku swoich implementacji, jednak wykorzystujących zbyt małą ilość kubitów, by można je było uznać za praktyczne, a więc zagrażające stosowanym dziś kryptosystemom. Warto wspomnieć, że istnieją inne algorytmy pozwalające na faktoryzację liczb naturalnych przy użyciu nieco innego modelu obliczeń kwantowych, przy czym ich najnowsze implementacje na komercyjnie dostępnych urządzeniach pozwalają na faktoryzację liczb rzędu kilkuset tysięcy.
Adiabatyczne obliczenia kwantowe zostały zaproponowane jako alternatywa dla obliczeń kwantowych opartych na paradygmacie sformułowanym przez Alana Turinga. Dziś wiemy, iż ta niesłychanie prosta koncepcja jest równoważna kwantowym obwodom logicznym. Idea adiabatycznych obliczeń kwantowych sprowadza się do na tyle powolnego zmieniania wybranego parametru układu, aby przez cały czas był on opisywany przez stan o najniższej chwilowej energii. Intencją tego działania jest, lub powinno być, przeprowadzenie układu ze znanego i łatwego do przygotowania stanu początkowego, który jest wektorem własnym Hamiltonianu 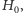 do stanu końcowego, który jest wektorem własnym operatora
do stanu końcowego, który jest wektorem własnym operatora 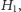 a który zawiera zakodowane rozwiązanie interesującego nas problemu, takie jak poszukiwana przez nas konfiguracja szkła spinowego. Ewolucję taką można otrzymać, zmieniając w sposób ciągły parametr
a który zawiera zakodowane rozwiązanie interesującego nas problemu, takie jak poszukiwana przez nas konfiguracja szkła spinowego. Ewolucję taką można otrzymać, zmieniając w sposób ciągły parametr ![s ∈[0,1]](/math/temat/informatyka/algorytmy/2017/11/25/Kwantowe_wyzarzanie/3x-cfb0cf652b77d3b74415a1a5b612d7d6b8d88c07-im-33,33,33-FF,FF,FF.gif) pomiędzy dwiema ustalonymi wartościami
pomiędzy dwiema ustalonymi wartościami 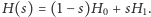

Dzięki uprzejmości D-Wave Systems
Jedynym dostępnym dziś na rynku komercyjnym urządzeniem, które realizuje opisaną powyżej procedurę, jest D-Wave 2X. Składa się on z chipa liczącego ponad 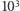 kubitów połączonych w strukturę zwaną chimerą. Fizycznie układ taki realizuje kwantowy model Isinga, a jego ewolucja w czasie to kwantowe wyżarzanie szkła spinowego. Dla
kubitów połączonych w strukturę zwaną chimerą. Fizycznie układ taki realizuje kwantowy model Isinga, a jego ewolucja w czasie to kwantowe wyżarzanie szkła spinowego. Dla 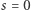 układ startuje ze stanu własnego
układ startuje ze stanu własnego 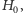 gdzie wszystkie kubity ułożone są w jednym kierunku. Konfiguracja taka jest łatwa do przygotowania, wystarczy włączyć dostatecznie silne pole magnetyczne. Następnie stopniowo i wolno zmniejszamy pole. W stanie końcowym pole magnetyczne staje się zaniedbywalne, a układ, opisany przez
gdzie wszystkie kubity ułożone są w jednym kierunku. Konfiguracja taka jest łatwa do przygotowania, wystarczy włączyć dostatecznie silne pole magnetyczne. Następnie stopniowo i wolno zmniejszamy pole. W stanie końcowym pole magnetyczne staje się zaniedbywalne, a układ, opisany przez 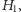 osiąga szukaną przez nas konfigurację, którą w drodze pomiaru możemy odczytać. Jeśli wyjściowym problemem byłoby poszukiwanie konfiguracji (klasycznego) szkła spinowego minimalizującej energię
osiąga szukaną przez nas konfigurację, którą w drodze pomiaru możemy odczytać. Jeśli wyjściowym problemem byłoby poszukiwanie konfiguracji (klasycznego) szkła spinowego minimalizującej energię 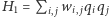 (na przykład optymalny podział grafu z poprzedniego rozdziału dla pewnych wartości
(na przykład optymalny podział grafu z poprzedniego rozdziału dla pewnych wartości 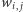 ), wówczas problem kwantowy w komputerze D-Wave otrzymuje się poprzez przypisanie zmiennej binarnej
), wówczas problem kwantowy w komputerze D-Wave otrzymuje się poprzez przypisanie zmiennej binarnej 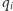 macierzy Pauliego
macierzy Pauliego 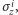 czyli
czyli  otrzymując
otrzymując 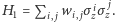 Naturalnym wyborem jest wtedy
Naturalnym wyborem jest wtedy 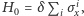 przy czym
przy czym 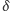 to pole magnetyczne, za pomocą którego "wyżarzamy" rozwiązanie.
to pole magnetyczne, za pomocą którego "wyżarzamy" rozwiązanie.
Takie podejście wiąże się z wieloma problemami. Aby dla 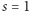 "trafić" w stan o najniższej energii, którego przecież szukamy, musimy w chwili
"trafić" w stan o najniższej energii, którego przecież szukamy, musimy w chwili 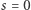 rozpocząć w stanie o najniższej energii (to w zasadzie jest proste), a potem zmieniać pole magnetyczne na tyle wolno, aby nie wzbudzić układu do stanu o wyższej energii - co już jest trudniejsze. Układ kwantowy pozostanie w stanie podstawowym, tylko gdy ewolucja przebiegać będzie adiabatycznie. Kiedy dynamika układu kwantowego jest wystarczająco wolna, aby adiabatyczne obliczenia kwantowe stały się możliwe? Niestety, odpowiedź na to pytanie jest w ogólności bardzo trudna. Pesymistycznie może się okazać, że czas chłodzenia nie jest wcale istotnie krótszy niż rozwiązanie badanego problemu przez komputer klasyczny.
rozpocząć w stanie o najniższej energii (to w zasadzie jest proste), a potem zmieniać pole magnetyczne na tyle wolno, aby nie wzbudzić układu do stanu o wyższej energii - co już jest trudniejsze. Układ kwantowy pozostanie w stanie podstawowym, tylko gdy ewolucja przebiegać będzie adiabatycznie. Kiedy dynamika układu kwantowego jest wystarczająco wolna, aby adiabatyczne obliczenia kwantowe stały się możliwe? Niestety, odpowiedź na to pytanie jest w ogólności bardzo trudna. Pesymistycznie może się okazać, że czas chłodzenia nie jest wcale istotnie krótszy niż rozwiązanie badanego problemu przez komputer klasyczny.
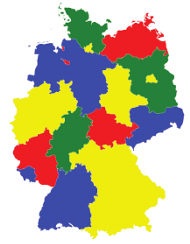
Kolejny przykład: kolorowanie mapy
Pokażemy teraz, w jaki sposób możemy wyżarzyć rozwiązanie problemu kolorowania mapy. Przypomnijmy jego sformułowanie: mapę podzieloną na regiony (na przykład polityczną mapę Europy lub mapę Niemiec podzieloną na landy) chcemy pokolorować tak, aby żadne dwa sąsiednie regiony nie były tej samej barwy. Okaże się zaraz, że problem ten można sprowadzić do poszukiwania optymalnej konfiguracji spinów w modelu Isinga i użyć komputera D-Wave do jego rozwiązania. Nasza mapa to graf, którego wierzchołki to regiony mapy, a krawędź łączy dwa wierzchołki wtedy i tylko wtedy, gdy odpowiadające im regiony sąsiadują na mapie. Otrzymany w ten sposób graf jest, oczywiście, planarny, a nasz problem sprowadza się do problemu kolorowania jego wierzchołków. Klasyczny rezultat z teorii grafów mówi nam, że wystarczą nam do tego cztery kolory.
Kolejnym krokiem jest przeformułowanie naszego problemu do postaci QUBO. Fundamentalną kwestią jest ustalenie kodowania kolorów. Do zakodowania w postaci zero-jedynkowej czterech kolorów wystarczą dwa bity. Okazuje się jednak, że wybranie takiego kodowania prowadziłoby do większego skomplikowania problemu. Zamiast tego kolor 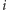 -tego regionu zakodujemy w postaci czterech bitów
-tego regionu zakodujemy w postaci czterech bitów 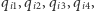 uznając, że region ten jest pokolorowany na
uznając, że region ten jest pokolorowany na 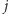 -ty kolor wtedy i tylko wtedy, gdy bit
-ty kolor wtedy i tylko wtedy, gdy bit 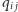 jest ustawiony na
jest ustawiony na 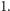 Oczywiście, takie kodowanie niesie ze sobą problemy - co jeśli dwa z czterech bitów będą ustawione na 1 albo wszystkie cztery będą miały wartość 0? Mając to na uwadze, musimy sformułować nasze QUBO tak, aby niepoprawne konfiguracje były "niekorzystne energetycznie". Innymi słowy, chcemy skonstruować funkcję kwadratową
Oczywiście, takie kodowanie niesie ze sobą problemy - co jeśli dwa z czterech bitów będą ustawione na 1 albo wszystkie cztery będą miały wartość 0? Mając to na uwadze, musimy sformułować nasze QUBO tak, aby niepoprawne konfiguracje były "niekorzystne energetycznie". Innymi słowy, chcemy skonstruować funkcję kwadratową 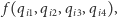 która jest zerem dokładnie wtedy, gdy jeden z jej argumentów jest jedynką oraz przyjmuje dodatnią wartość w pozostałych przypadkach. Funkcją taką jest
która jest zerem dokładnie wtedy, gdy jeden z jej argumentów jest jedynką oraz przyjmuje dodatnią wartość w pozostałych przypadkach. Funkcją taką jest 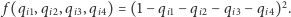 Podnosząc nawias do kwadratu i zaniedbując stałą (dodawanie stałej do QUBO nie zmienia problemu optymalizacyjnego), możemy przyjąć
Podnosząc nawias do kwadratu i zaniedbując stałą (dodawanie stałej do QUBO nie zmienia problemu optymalizacyjnego), możemy przyjąć
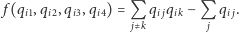 |
(2) |
Tak skonstruowana funkcja 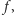 dodana z dużą stałą dodatnią do naszej funkcji celu (energii), powinna zapewnić nam znalezienie optymalnego rozwiązania o dopuszczalnej konfiguracji.
dodana z dużą stałą dodatnią do naszej funkcji celu (energii), powinna zapewnić nam znalezienie optymalnego rozwiązania o dopuszczalnej konfiguracji.
Pozostaje skonstruowanie tego fragmentu funkcji celu, który spenalizuje rozwiązania, w których sąsiednie regiony są pokolorowane w ten sam sposób. Jeżeli 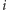 -ty oraz
-ty oraz 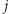 -ty region sąsiadują, to dla żadnego
-ty region sąsiadują, to dla żadnego 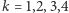 nie może spełniona być równość
nie może spełniona być równość 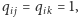 lub równoważnie
lub równoważnie 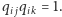 Kolejnym składnikiem naszej "energii" jest więc
Kolejnym składnikiem naszej "energii" jest więc 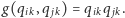
Ostatecznie zatem, poszukujemy konfiguracji szkła spinowego minimalizującego energię
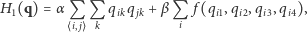 |
(3) |
przy czym 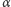 i
i 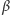 to pewne stałe dodatnie, a notacja
to pewne stałe dodatnie, a notacja 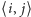 oznacza sąsiadujące regiony o numerach
oznacza sąsiadujące regiony o numerach 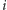 oraz
oraz 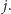 Teraz wystarczy dodać
Teraz wystarczy dodać 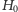 i wyżarzać rozwiązanie.
i wyżarzać rozwiązanie.
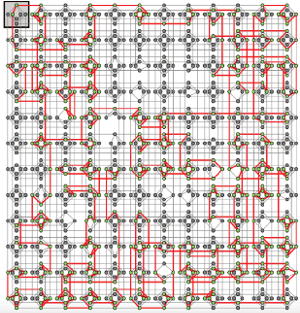
Koncepcyjnie mamy już skonstruowany problem optymalizacyjny, ale, niestety, dla większości map nie wystarczy to do rozwiązania go na maszynie D-Wave. Powodem jest topologia grafu tworzonego przez kubity - graf ten, mimo sporej liczby kubitów, jest dość rzadki, ma stosunkowo mało krawędzi, co widać na rysunku na tylnej okładce. Będziemy musieli się więc uciec do tak zwanego embeddingu. Idea jest prosta, ale w praktyce często wymagająca w realizacji: łączymy kilka kubitów fizycznych w jeden logiczny. Taki logiczny kubit będzie miał więcej sąsiadów niż każdy ze składowych fizycznych kubitów. Wynik naszych starań widzimy na rysunku.
Łyżka dziegciu
Zaskakująco wiele problemów znanych z klasycznej teorii obliczeń daje się wyrazić w języku spinowego szkła Isinga. W szczególności można to zrobić w przypadku wszystkich 21 problemów Karpa. Czy to oznacza, że ich rozwiązanie można zawsze wyżarzyć, używając do tego maszyn D-Wave? Niestety, jeszcze nie. Jednym z powodów jest wspomniane już ograniczenie narzucane przez topologię chimery ukrytej w maszynie D-Wave: zaskakująco niewiele spośród naprawdę ciekawych problemów daje się zapisać na takim typie grafu. Co więcej, nawet jeśli okazuje się to możliwe, wcale nie jest oczywiste, czy warto to robić (może się okazać, że czas rozwiązania jest wciąż porównywalny z najlepszymi rozwiązaniami dla komputerów klasycznych). Wyniki intensywnych badań prowadzonych przez fizyków przy użyciu maszyn D-Wave oraz nad maszynami D-Wave wskazują, że oczekiwane "kwantowe przyśpieszenie" wyżarzania kwantowego nie jest wcale oczywiste. Uniwersalnym kandydatem na winnego wszelkich niepowodzeń informatyki kwantowej jest wszechobecna dekoherencja, i choć w porównaniu do wnętrza maszyn D-Wave przestrzeń kosmiczna jest całkiem ciepłym miejscem, nie można wykluczyć, że D-Wave pracuje w reżimie nie dość adiabatycznym. Nie można jednak wykluczyć, że problemem znów jest chimera, gdyż pechowym zbiegiem okoliczności, dla tego typu grafów wyżarzanie kwantowe jest nie lepsze niż klasyczne algorytmy, takie jak choćby symulowane wyżarzanie lub dynamika molekularna. Maszyny D-Wave rosną jak na drożdżach, na chimerę w ich trzewiach składa się coraz to więcej kubitów. To dobrze, gdyż daje to użytkownikom możliwość wykorzystania skutecznego embeddingu i tworzenia kubitów logicznych. Z drugiej jednak strony dopiero możliwość implementacji szerszej klasy mniej chimerycznych grafów da nam odpowiedź, czy w przyszłości będziemy wyżarzać kwantowo rozwiązanie naszych problemów optymalizacyjnych.