W 1994, ale też i teraz, w 2017 roku, po prostu nie umiemy rozkładać szybko liczb na czynniki pierwsze. A na trudności faktoryzacji opiera się m.in. kryptologia, najbardziej znany kryptosystem RSA dałby się łatwo łamać, gdybyśmy umieli szybko rozkładać liczby na czynniki pierwsze. Drugim najbardziej popularnym problemem, na którego trudności opiera się wiele w kryptologii, jest problem logarytmu dyskretnego (dla danych 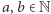i liczby pierwszej 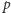znajdź 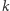takie, że 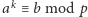). Warto wiedzieć, że w tym samym artykule Shor udowodnił również, że komputer kwantowy umie rozwiązywać problem logarytmu dyskretnego w czasie wielomianowym. Algorytm Shora nie tylko zainspirował intensywne badania w tej dziedzinie, ale chyba do tej pory jest najbardziej znanym i celebrowanym algorytmem kwantowym.

W tym artykule postaramy się zrozumieć najistotniejsze idee w algorytmie Shora. Niektóre szczegóły techniczne pominiemy, gdyż tłumaczenie wszystkiego zajęłoby raczej kilkanaście stron niż kilka.

Sprecyzujmy problem. Dostajemy liczbę 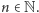W naszych rozważaniach skupimy się na przypadku, gdy 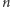jest iloczynem dwóch liczb pierwszych, tj. 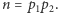Ten przypadek jest również trudny (nie ma dla niego żadnych szybko działających heurystyk), a algorytm Shora w ogólności działa prawie identycznie, jak dla tego przypadku. Nasz cel to znaleźć liczby 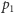i 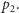Po pierwsze powiedzmy sobie od razu, że algorytm Shora jest oparty na losowości. Uruchomiony wiele razy z pewnym dużym (bliskim 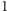) prawdopodobieństwem znajdzie rozkład 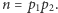Myślmy, że zarówno 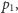jak i 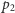mają po 100 cyfr, wtedy będziemy mieli odpowiednie wyobrażenie o tym, co się da, a czego nie da się szybko zrobić.

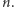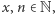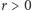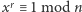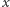Pierwszy krok, niemający jeszcze żadnego związku z kwantami, to redukcja faktoryzacji do problemu rzędu elementu modulo Problem ten, dla danych pyta o najmniejsze naturalne takie, że (takie nazywamy rzędem modulo 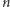). Przy założeniu, że umiemy w czasie wielomianowym znajdować rząd elementu (wszędzie tu używana jest losowość, więc przestaniemy się na niej skupiać, a czasem nawet o niej wspominać), pokażemy, jak rozłożyć na czynniki w czasie wielomianowym. Rozważmy 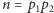i wylosujmy liczbę ze zbioru 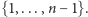Jeśli 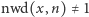(co możemy szybko sprawdzić algorytmem Euklidesa), to świetnie, bo wtedy 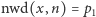albo 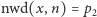i znaleźliśmy rozkład. Ale to się zdarza rzadko. Załóżmy więc, że 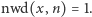Można wykazać (nie bardzo trudno, szczegóły pominiemy), że dla co najmniej jednej czwartej wylosowanych 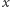zachodzą następujące dwa warunki: 1) 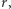czyli rząd 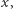jest parzysty, 2) 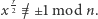Dla takiego 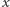mamy 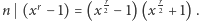Jednak skoro nie dzieli żadnego z dwóch nawiasów, to musi być tak, że 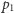dzieli jeden z nich, a 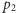drugi. Zatem 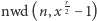jest równe a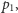lbo albo 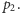Łatwo je obliczyć algorytmem Euklidesa, a tym samym znaleźć rozkład A więc wystarczy skupić się na znajdowaniu rzędu liczby 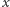modulo 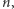co zrobimy przy użyciu algorytmu kwantowego.

Ustalmy pewne 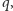które należy do przedziału oraz jest potęgą dwójki, niech 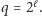Nasz algorytm na wejściu będzie miał 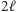drutów, czyli będzie operował na 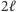kubitach (albo jeszcze inaczej: stan pamięci może być opisany przez wektor długości 1 z 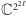). Te 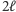drutów podzielimy na dwa segmenty po 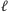drutów. Zaczynamy od stanu pamięci równego 0 na wszystkich kubitach. Czyli, formalnie rzecz biorąc, jest to stan 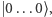gdzie ciąg zer ma długość 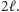My jednak na potrzeby naszego algorytmu będziemy o nim myśleli jako o 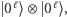co będziemy zapisywać w skrócie jako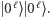

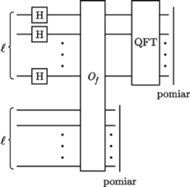
Cały obwód kwantowy realizujący algorytm Shora przedstawiony jest na rysunku. Wchodzi do niego 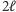drutów po lewej, do których po kolei aplikowane są bramki kwantowe i na końcu wykonywany jest pomiar. Fakt, że algorytm jest wielomianowy, oznacza, że w obwodzie jest wielomianowo wiele podstawowych bramek (czyli bramek Hadamarda 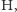obrotu 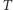i kontrolowanej negacji CNOT, z których składamy wszystkie macierze unitarne, potrzebne do obliczeń). Teraz szczegółowo opiszemy, co dzieje się po kolei (od lewej).

Najpierw robimy to, co często robią na początek algorytmy kwantowe, czyli zamieniamy stan "same zera" na superpozycję wszystkich możliwych stanów bazowych, każdy z równym prawdopodobieństwem. Tyle, że my teraz zrobimy to tylko na pierwszych 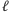kubitach, tj. w pierwszym segmencie. Aby to zrobić, używamy, jak zawsze w takim przypadku, bramek Hadamarda

Bramka 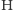przekształc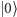a na 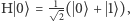czyli na superpozycję 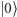i 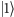z równym prawdopodobieństwem. Jeśli zastosujemy bramkę 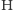do każdego z pierwszych 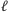kubitów, to stan 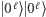zostanie przekształcony na stan 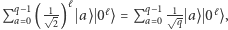gdzie przez 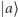rozumiemy stan określony przez binarną reprezentację 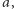np. dla przez 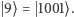Formalnie rzecz biorąc, powyżej przyłożyliśmy do aktualnego stanu przekształcenie będące produktem 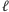macierzy Hadamarda H i 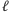macierzy identycznościowych I. Jednak warto patrzeć na to intuicyjnie, jako na przyłożenie bramki Hadamarda do każdego kubitu oddzielnie, bo takie jest właśnie znaczenie produktu tensorowego.

Następnie w algorytmie przykładamy do wszystkich drutów bramkę, która liczy funkcję 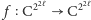(czyli z 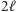kubitów w 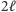kubitów) taką, że

Przypomnijmy, że 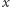to nasza wylosowana liczba ze zbioru 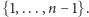Na rysunku obwód obliczający funkcję 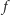oznaczamy przez 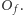Sprawdzenie, że obliczenie funkcji 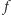jest unitarne oraz że da się je zrealizować obwodem o wielomianowej liczbie małych bramek, nie jest specjalnie trudne. Tutaj jednak pominiemy szczegóły. A więc po przejściu przez bramkę 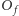stan jest następującą superpozycją:

Teraz wykonujemy pomiar na drugim segmencie, czyli na drugich 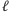kubitach. W wyniku pomiaru zmierzona zostaje jakaś (nie wiemy z góry jaka!) wartość 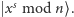Przy czym nie wiadomo wcale, czy na pierwszych 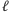kubitach jest wartość 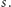Może być również tak, że jest tam wartość 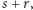gdyż 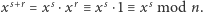Podobnie może być tam wartość 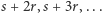Tak jak po każdym pomiarze, teraz stan układu jest superpozycją tych stanów bazowych sprzed pomiaru, które są zgodne z pomiarem.

W dalszej części rozważa się dwa przypadki. Pierwszy, gdy 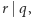jest łatwiejszy, a drugi, gdy 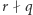trudniejszy. My przyjrzyjmy się pierwszemu, bo idea jest w obu przypadkach podobna, tylko w drugim jest więcej szczegółów technicznych. W tym przypadku z pomiarem 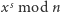(dla 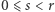) zgodne są wartości 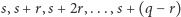na pierwszych 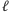kubitach. Zatem po pomiarze stan układu na pierwszych 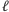kubitach jest postaci

Widać teraz, że jest jakoś związane ze stanem układu. Pytanie tylko, jak je z niego wydobyć. Jeśli zmierzymy po prostu wartość tych kubitów, to otrzymamy pewną liczbę 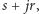która będzie jakąś liczbą ze zbioru 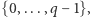wiele nam nie powie. Nie znamy przecież 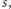żeby móc obliczyć 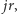a tym bardziej nie znamy 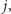żeby obliczyć z 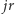wartość 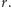Musimy więc postępować inaczej.

Tu w sukurs przychodzi nam dziedzina, która wielu Czytelnikom zapewne wcale nie kojarzy się z faktoryzacją liczb pierwszych. Przyjrzyjmy się jeszcze raz naszemu pytaniu, z nieco innej strony. Możemy pomyśleć o naszej superpozycji jako o ciągu wartości 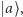dla których przy większości jest współczynnik 0, ale dla niektórych niezerowy współczynnik 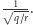Te wartości o niezerowych współczynnikach powtarzają się co i chcemy odkryć, z jakim okresem to robią. Wróćmy na chwilę do świata niekwantowego i zastanówmy się, co należy robić w takich sytuacjach, jak znaleźć okres pewnego okresowego zjawiska. Zauważmy, że nasze ucho robi to przez cały czas. Dźwięk, który słyszymy, rozkłada się bowiem na wiele składowych o różnych częstotliwościach. Ucho właśnie rozkłada dźwięk na składowe, które wyglądają jak sinusy i kosinusy. To, co robi, nazywa się w matematyce transformatą Fouriera. Okazuje się, że każdą funkcję okresową da się rozłożyć na nieskończoną sumę sinusów i kosinusów. Podobnie robi się, gdy mamy sygnał, który nie jest ciągły, lecz dyskretny. Tylko, że wtedy rozkładamy na skończoną sumę próbkowań kosinusów. Czytelnik Zapoznany Z Algebrą Liniową może sobie wyobrażać oba przekształcenia jako wyrażanie funkcji okresowej (bądź jej próbkowania) po prostu w innej bazie, złożonej z sinusów i kosinusów (bądź ich próbkowań). Ciekawostką może być, że ta sama transformata jest wykorzystywana w innych miejscach informatyki, np. w formatach jpeg lub mpeg.

A więc w świecie kwantowym, jeśli chcemy odnaleźć coś w stylu okresu w naszym stanie, też powinniśmy zastosować transformatę Fouriera, tylko że kwantową. Szczęśliwie rzeczywiście istnieje kwantowa transformata Fouriera (QFT - quantum Fourier transform), która okazuje się unitarna i daje się zaimplementować za pomocą wielomianowej liczby podstawowych bramek kwantowych. Przyłożenie jej do naszej konfiguracji 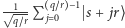na wyjściu daje współczynniki przy odpowiednich okresach. Dostajemy pewną superpozycję 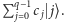Okazuje się, że dla przypadku gdy 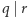współczynniki 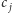są niezerowe jedynie dla 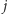będących wielokrotnościami 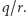A więc możemy teraz wykonać pomiar i jesteśmy pewni, że otrzymaliśmy jakąś wielokrotność 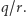Gdy wykonamy wiele (ale wielomianowo wiele) takich pomiarów i weźmiemy minimum albo 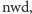to obliczymy z dużym prawdopodobieństwem 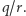A zatem poznamy również i rząd 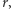co kończy naszą opowieść.

Czytelnikom Zainteresowanym Szczegółami polecamy oryginalny artykuł Petera Shora dostępny pod adresem: arxiv.org/abs/quant-ph/9508027.