Dlaczego problem 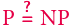 jest tak trudny?
jest tak trudny?
24 maja 2000 roku Instytut Matematyczny Claya ogłosił listę siedmiu Problemów Milenijnych, czyli zagadnień, które zostały uznane za najważniejsze otwarte problemy matematyczne opierające się rozwiązaniom od lat. Wśród nich był jeden problem zaliczany do informatyki teoretycznej, o którym wielu Czytelników zapewne słyszało. Chodzi oczywiście o tytułowy problem: "Czy P=NP"? Jest on powszechnie uznawany za najważniejsze pytanie informatyki teoretycznej.
Problem nazywamy decyzyjnym, jeśli odpowiedź to "tak" lub "nie" (a nie np. liczba). Klasa 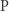 (od Polynomial time) zawiera te problemy, które dadzą się rozwiązać w czasie wielomianowym. Definicja klasy
(od Polynomial time) zawiera te problemy, które dadzą się rozwiązać w czasie wielomianowym. Definicja klasy 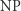 (od Nondeterministic Polynomial time) jest nieco bardziej złożona. Powiemy, że problem
(od Nondeterministic Polynomial time) jest nieco bardziej złożona. Powiemy, że problem 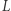 należy do
należy do 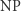 , o ile dla każdego możliwego wejścia
, o ile dla każdego możliwego wejścia 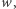 na które odpowiedź jest "tak", istnieje świadek tej pozytywnej odpowiedzi
na które odpowiedź jest "tak", istnieje świadek tej pozytywnej odpowiedzi 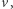 co najwyżej wielomianowo większy niż
co najwyżej wielomianowo większy niż 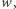 taki, że gdy dostaniemy parę
taki, że gdy dostaniemy parę 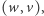 to możemy w czasie wielomianowym potwierdzić, że istotnie odpowiedź na
to możemy w czasie wielomianowym potwierdzić, że istotnie odpowiedź na 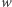 to "tak". Intuicyjnie więc
to "tak". Intuicyjnie więc 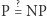 pyta mniej więcej, czy każdy problem, dla którego można sprawdzić poprawność odpowiedzi szybko (w czasie wielomianowym), można również rozwiązać szybko (w czasie wielomianowym). Już w latach 50. problem ten pojawiał się w dyskusjach, ale precyzyjnie zdefiniował go w 1971 roku Stephen Cook. Od tej pory jest otwarty, mimo że naprawdę wiele osób próbowało go rozwiązać.
pyta mniej więcej, czy każdy problem, dla którego można sprawdzić poprawność odpowiedzi szybko (w czasie wielomianowym), można również rozwiązać szybko (w czasie wielomianowym). Już w latach 50. problem ten pojawiał się w dyskusjach, ale precyzyjnie zdefiniował go w 1971 roku Stephen Cook. Od tej pory jest otwarty, mimo że naprawdę wiele osób próbowało go rozwiązać.
Dlaczego jednak uważamy ten problem za aż tak ważny i ciekawy? Przecież jest wiele starych problemów, których nikt jeszcze nie rozwiązał. Można na to pytanie odpowiedzieć na kilka sposobów. Po pierwsze, jest bardzo wiele praktycznych problemów, o których wiemy, że należą do klasy 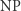 , jednak nie znamy dla nich żadnego algorytmu wielomianowego. Często rozważanym przykładem jest tzw. problem komiwojażera, w którym mamy dany graf o
, jednak nie znamy dla nich żadnego algorytmu wielomianowego. Często rozważanym przykładem jest tzw. problem komiwojażera, w którym mamy dany graf o  wierzchołkach (reprezentujących miasta), a na każdej krawędzi liczbę, która oznacza, ile czasu potrzebuje komiwojażer, aby przejechać między tymi właśnie miastami. Pytanie brzmi, czy może on objechać wszystkie miasta i wrócić do domu w zadanym czasie (lub szybciej). Łatwo zauważyć, że istotnie należy on do
wierzchołkach (reprezentujących miasta), a na każdej krawędzi liczbę, która oznacza, ile czasu potrzebuje komiwojażer, aby przejechać między tymi właśnie miastami. Pytanie brzmi, czy może on objechać wszystkie miasta i wrócić do domu w zadanym czasie (lub szybciej). Łatwo zauważyć, że istotnie należy on do 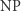 , świadkiem jest tutaj samo rozwiązanie, czyli cykl o wystarczająco małym czasie przejazdu. Innym przykładem, ważnym w dalszej części artykułu, jest problem spełnialności formuł (znany jako SAT od angielskiego satisfiability - spełnialność). Rozważamy w tym przypadku formuły logiczne zawierające
, świadkiem jest tutaj samo rozwiązanie, czyli cykl o wystarczająco małym czasie przejazdu. Innym przykładem, ważnym w dalszej części artykułu, jest problem spełnialności formuł (znany jako SAT od angielskiego satisfiability - spełnialność). Rozważamy w tym przypadku formuły logiczne zawierające 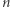 zmiennych:
zmiennych: 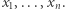 Możemy założyć, że formuła jest zawsze koniunkcją klauzul
Możemy założyć, że formuła jest zawsze koniunkcją klauzul 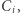 czyli postaci
czyli postaci 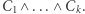 Każda klauzula natomiast jest alternatywą zmiennych
Każda klauzula natomiast jest alternatywą zmiennych 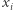 lub ich negacji
lub ich negacji 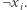 Przykładowa formuła wygląda więc tak:
Przykładowa formuła wygląda więc tak:
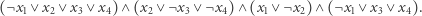 |
Pytanie brzmi, czy istnieją takie wartości 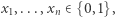 dla których formuła jest prawdziwa. W naszym przykładzie istnieją: są to, na przykład,
dla których formuła jest prawdziwa. W naszym przykładzie istnieją: są to, na przykład, 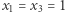 oraz
oraz 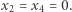 SAT należy do
SAT należy do 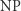 , bo świadkiem spełnialności jest tu po prostu takie wartościowanie zmiennych, które spełnia formułę. A więc, tak jak i wcześniej, świadkiem jest obiekt, o którego istnienie pytamy. Jest to częste zjawisko, ale wcale nie zawsze świadek musi być takiej postaci. Wiele praktycznych problemów da się przepisać jako problem spełnialności formuły powyższej postaci, więc bardzo przydatne byłoby umieć rozwiązywać je szybko, najlepiej w czasie wielomianowym. Niestety, nie znamy takich metod, a najlepsze znane algorytmy działają w czasie wykładniczym. Znaczy to, że nie są istotnie lepsze od bezmyślnego podstawiania wszystkich możliwych
, bo świadkiem spełnialności jest tu po prostu takie wartościowanie zmiennych, które spełnia formułę. A więc, tak jak i wcześniej, świadkiem jest obiekt, o którego istnienie pytamy. Jest to częste zjawisko, ale wcale nie zawsze świadek musi być takiej postaci. Wiele praktycznych problemów da się przepisać jako problem spełnialności formuły powyższej postaci, więc bardzo przydatne byłoby umieć rozwiązywać je szybko, najlepiej w czasie wielomianowym. Niestety, nie znamy takich metod, a najlepsze znane algorytmy działają w czasie wykładniczym. Znaczy to, że nie są istotnie lepsze od bezmyślnego podstawiania wszystkich możliwych 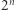 wartości na zmienne
wartości na zmienne 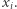 Co ciekawe, oba powyższe problemy są NP-zupełne, co oznacza, że każdy inny problem z klasy
Co ciekawe, oba powyższe problemy są NP-zupełne, co oznacza, że każdy inny problem z klasy 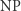 da się przeformułować na SAT albo na problem komiwojażera niewiele (co najwyżej wielomianowo) większej wielkości. Oznacza to, że gdybyśmy umieli rozwiązać jakiś problem
da się przeformułować na SAT albo na problem komiwojażera niewiele (co najwyżej wielomianowo) większej wielkości. Oznacza to, że gdybyśmy umieli rozwiązać jakiś problem 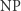 -zupełny (np. SAT), to wszystkie inne problemy z klasy
-zupełny (np. SAT), to wszystkie inne problemy z klasy 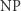 rozwiązalibyśmy również w czasie wielomianowym (poprzez sformułowanie w postaci SATa, a potem rozwiązanie go). A to oznaczałoby, że
rozwiązalibyśmy również w czasie wielomianowym (poprzez sformułowanie w postaci SATa, a potem rozwiązanie go). A to oznaczałoby, że 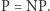 Ta właśnie cecha problemów
Ta właśnie cecha problemów 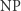 -zupełnych świadczy o ich znaczeniu: wystarczy rozwiązać jeden z nich, a wiemy, że
-zupełnych świadczy o ich znaczeniu: wystarczy rozwiązać jeden z nich, a wiemy, że 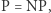 z drugiej strony, oczywiście, jeśli tylko jeden z nich nie należy do
z drugiej strony, oczywiście, jeśli tylko jeden z nich nie należy do 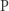 , to
, to 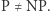
Gdybyśmy umieli rozwiązywać SAT w czasie wielomianowym, to wiele problemów rozwiązalibyśmy dużo szybciej. To dobrze. Jednak byłyby też złe strony tej sytuacji. Większość szyfrów opiera się na tym, że pewne obliczenia wymagają dużo czasu i nie są znane metody istotnie lepsze od sprawdzania wszystkich możliwych wartości (jak wyżej dla wartości zmiennych 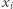 ). Gdyby jednak
). Gdyby jednak 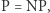 to te obliczenia już nie potrzebowałyby tyle czasu i większość szyfrów przestałaby być bezpieczna. To źle. To kolejna motywacja do zrozumienia, czy
to te obliczenia już nie potrzebowałyby tyle czasu i większość szyfrów przestałaby być bezpieczna. To źle. To kolejna motywacja do zrozumienia, czy 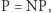 czy też nie. I to trochę innego rodzaju, bo w tym przypadku, jeśli zrozumiemy, że
czy też nie. I to trochę innego rodzaju, bo w tym przypadku, jeśli zrozumiemy, że 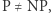 to też mamy zysk: wiemy, że niektóre szyfry są chociaż trochę bezpieczne. Te dwie motywacje nie są jedynymi powodami, dla których chcemy znać odpowiedź. To tylko poszlaki, że problem jest naprawdę ważny i fundamentalny. Być może najważniejszą przyczyną jest przekonanie, które stoi u źródeł nauk podstawowych, że zrozumienie tak istotnego problemu, niezależnie od wyniku, może skutkować nieprzewidywalnymi wręcz korzyściami. Tak jak to było z odkryciem przez Watsona i Cricka, że DNA ma strukturę podwójnej helisy.
to też mamy zysk: wiemy, że niektóre szyfry są chociaż trochę bezpieczne. Te dwie motywacje nie są jedynymi powodami, dla których chcemy znać odpowiedź. To tylko poszlaki, że problem jest naprawdę ważny i fundamentalny. Być może najważniejszą przyczyną jest przekonanie, które stoi u źródeł nauk podstawowych, że zrozumienie tak istotnego problemu, niezależnie od wyniku, może skutkować nieprzewidywalnymi wręcz korzyściami. Tak jak to było z odkryciem przez Watsona i Cricka, że DNA ma strukturę podwójnej helisy.
Dochodzimy teraz do pytania, o którym tak naprawdę chcę opowiedzieć, czyli: skoro uważamy ten problem za tak ważny i tylu ludzi bardzo się stara, to dlaczego wciąż jest nierozwiązany? Można by uznać, że jest to pytanie głupie: jak to dlaczego - jest po prostu trudny. Nie pozostawajmy jednak na tym poziomie odpowiedzi, bo historia jest dużo bardziej subtelna. Już przez ponad 45 lat ludzie próbowali rozwiązać problem, pewne metody rozwijały się, ale nie udawało się nimi rozwiązać 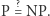 Więc zadawali sobie pytanie: "dlaczego nam się nie udaje?". I często tym sposobem dochodzili do wniosku, że pewne metody po prostu nie mogą działać. Historia tych badań jest fascynująca i może nam bardzo wiele powiedzieć o teorii złożoności, a także chociaż trochę wytłumaczyć, dlaczego
Więc zadawali sobie pytanie: "dlaczego nam się nie udaje?". I często tym sposobem dochodzili do wniosku, że pewne metody po prostu nie mogą działać. Historia tych badań jest fascynująca i może nam bardzo wiele powiedzieć o teorii złożoności, a także chociaż trochę wytłumaczyć, dlaczego 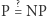 jest aż tak trudny i jakie bariery stoją na drodze.
jest aż tak trudny i jakie bariery stoją na drodze.
Wszystko zaczęło się w latach 70. Po tym, jak Cook zadał pytanie, matematycy próbowali je rozwiązać. Naturalną techniką była wtedy tak zwana metoda diagonalizacji. Wiele pierwszych rezultatów z teorii złożoności (czyli dziedziny zajmującej się klasyfikacją problemów na bardziej złożone i mniej złożone) używa właśnie tej metody. Użyta jest np. w dowodach nierozstrzygalności problemu stopu, twierdzenia (dużo starszego) o tym, że liczb rzeczywistych jest więcej niż naturalnych, albo mniej znanych twierdzeń o hierarchii czasowej i pamięciowej. Niech język będzie zbiorem słów nad pewnym ustalonym alfabetem, czyli ciągów liter z tego alfabetu. Rozważmy maszyny, które dostają słowo, wykonują jakieś obliczenie i odpowiadają "tak" lub "nie", typowy przykład to maszyny Turinga, być może z jakimiś ograniczeniami (jak działanie w czasie wielomianowym). Zbiór słów, dla których maszyna 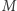 odpowie "tak", nazywamy językiem tej maszyny, oznaczamy go
odpowie "tak", nazywamy językiem tej maszyny, oznaczamy go 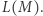 Rozważmy teraz dwie klasy maszyn
Rozważmy teraz dwie klasy maszyn 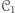 i
i 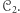 Aby wykazać, że maszyny z
Aby wykazać, że maszyny z 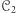 opisują pewne języki, które nie są opisywane przez maszyny z
opisują pewne języki, które nie są opisywane przez maszyny z 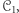 wystarczy wskazać taką maszynę
wystarczy wskazać taką maszynę 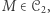 że dla dowolnej maszyny
że dla dowolnej maszyny 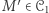 istnieje takie słowo
istnieje takie słowo 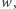 iż maszyny
iż maszyny 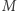 i
i 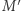 potraktują je inaczej (jedna z nich powie "tak", a druga "nie"). Tę właśnie metodę nazywamy diagonalizacją. Okazuje się, że większość dowodów, które używają tej metody, podlega relatywizacji. Aby powiedzieć, co to oznacza, opowiemy najpierw o wyroczni. Rozważmy jakąś wyrocznię
potraktują je inaczej (jedna z nich powie "tak", a druga "nie"). Tę właśnie metodę nazywamy diagonalizacją. Okazuje się, że większość dowodów, które używają tej metody, podlega relatywizacji. Aby powiedzieć, co to oznacza, opowiemy najpierw o wyroczni. Rozważmy jakąś wyrocznię 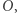 która odpowiada "tak" lub "nie" na pewne pytania poprawnie i za darmo. Możemy dodać maszynie możliwość zadawania pytań do takiej wyroczni. Przykładowo wyrocznia mogłaby odpowiadać na pytanie, czy dana liczba jest potęgą liczby pierwszej. Widać wtedy, że maszyna, która miałaby za zadanie stwierdzić, czy dana liczba jest pierwsza, miałaby, być może, ułatwione zadanie, gdyby mogła pytać taką wyrocznię. Klasę maszyn
która odpowiada "tak" lub "nie" na pewne pytania poprawnie i za darmo. Możemy dodać maszynie możliwość zadawania pytań do takiej wyroczni. Przykładowo wyrocznia mogłaby odpowiadać na pytanie, czy dana liczba jest potęgą liczby pierwszej. Widać wtedy, że maszyna, która miałaby za zadanie stwierdzić, czy dana liczba jest pierwsza, miałaby, być może, ułatwione zadanie, gdyby mogła pytać taką wyrocznię. Klasę maszyn 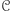 z możliwością korzystania z wyroczni
z możliwością korzystania z wyroczni 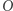 oznaczmy przez
oznaczmy przez 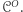 Powiemy, że dowód, iż maszyny z
Powiemy, że dowód, iż maszyny z 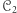 rozpoznają więcej języków niż maszyny z
rozpoznają więcej języków niż maszyny z 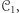 się relatywizuje, jeśli dla dowolnej wyroczni
się relatywizuje, jeśli dla dowolnej wyroczni 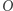 ten dowód pokazuje również, że maszyny z
ten dowód pokazuje również, że maszyny z 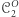 rozpoznają więcej języków niż maszyny z
rozpoznają więcej języków niż maszyny z 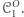 Jak powiedzieliśmy, zasadniczo dowody używające diagonalizacji się relatywizują. I dlatego przełomem było twierdzenie, które w roku 1975 udowodnili Baker, Gill i Solovay. Pokazali oni, że istnieje taka wyrocznia
Jak powiedzieliśmy, zasadniczo dowody używające diagonalizacji się relatywizują. I dlatego przełomem było twierdzenie, które w roku 1975 udowodnili Baker, Gill i Solovay. Pokazali oni, że istnieje taka wyrocznia 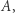 że
że 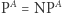 oraz taka wyrocznia
oraz taka wyrocznia 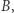 że
że 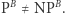 Oznacza to, że żaden dowód, który się relatywizuje, na pewno nie pokaże, że
Oznacza to, że żaden dowód, który się relatywizuje, na pewno nie pokaże, że 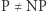 (bo jest wyrocznia
(bo jest wyrocznia 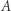 ) ani że
) ani że 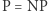 (bo jest wyrocznia
(bo jest wyrocznia 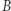 ). Jeśli chcemy rozwiązać
). Jeśli chcemy rozwiązać 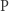
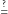
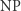 , to musimy iść inną drogą.
, to musimy iść inną drogą.
Ten wynik spowodował, że społeczność badaczy teorii złożoności zarzuciła metody diagonalizacji przy rozwiązywaniu problemu 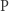
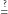
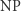 . W zasadzie słusznie, ale ruch ten był, być może, zbyt radykalny. Można bowiem wyobrazić sobie, że diagonalizacja jest tylko jednym z argumentów w dowodzie i wówczas cały dowód się nie relatywizuje. W każdym razie mniej więcej w tamtym czasie popularne zaczęły być obwody logiczne, to z nimi wiązano teraz nadzieję na postęp w kwestii problemu
. W zasadzie słusznie, ale ruch ten był, być może, zbyt radykalny. Można bowiem wyobrazić sobie, że diagonalizacja jest tylko jednym z argumentów w dowodzie i wówczas cały dowód się nie relatywizuje. W każdym razie mniej więcej w tamtym czasie popularne zaczęły być obwody logiczne, to z nimi wiązano teraz nadzieję na postęp w kwestii problemu 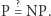 Obwód logiczny o
Obwód logiczny o 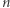 wejściach i jednym wyjściu oblicza funkcję
wejściach i jednym wyjściu oblicza funkcję 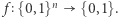 Wszystko można zakodować jako ciąg zer i jedynek, natomiast jedynkę na wyjściu traktować jako odpowiedź "tak", a zero jako odpowiedź "nie". A zatem obwód logiczny jest dobrą alternatywą dla maszyn i można też używać go do opisu języków. Pomiędzy
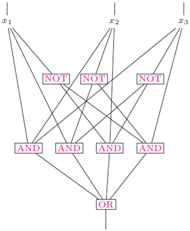
Wszystko można zakodować jako ciąg zer i jedynek, natomiast jedynkę na wyjściu traktować jako odpowiedź "tak", a zero jako odpowiedź "nie". A zatem obwód logiczny jest dobrą alternatywą dla maszyn i można też używać go do opisu języków. Pomiędzy  wejściami a wyjściem obwód ma bramki jednego z trzech typów: AND, OR oraz NOT. Bramki AND i OR mogą mieć wiele wejść, a wyjście mają jedno, na którym zwracają koniunkcję (AND) lub alternatywę (OR) wejść. Bramka NOT ma jedno wejście i jedno wyjście, na którym wypuszcza zanegowane wejście. Można składać z tych bramek dowolnie skomplikowane funkcje, na rysunkuprzedstawiono obwód dla funkcji
wejściami a wyjściem obwód ma bramki jednego z trzech typów: AND, OR oraz NOT. Bramki AND i OR mogą mieć wiele wejść, a wyjście mają jedno, na którym zwracają koniunkcję (AND) lub alternatywę (OR) wejść. Bramka NOT ma jedno wejście i jedno wyjście, na którym wypuszcza zanegowane wejście. Można składać z tych bramek dowolnie skomplikowane funkcje, na rysunkuprzedstawiono obwód dla funkcji 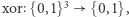 która zwraca sumę wejść modulo dwa. Co prawda, każdą funkcję można opisać pewnym obwodem (Ambitnego Czytelnika zachęcamy do wykazania tego faktu), ale już gdy ograniczymy pewne parametry obwodów, to nie wszystkie funkcje dadzą się opisać i sytuacja staje się znacznie ciekawsza. Przykładowo jeden z ważniejszych wyników tamtego okresu (1983 rok) to dowód, że ciąg funkcji
która zwraca sumę wejść modulo dwa. Co prawda, każdą funkcję można opisać pewnym obwodem (Ambitnego Czytelnika zachęcamy do wykazania tego faktu), ale już gdy ograniczymy pewne parametry obwodów, to nie wszystkie funkcje dadzą się opisać i sytuacja staje się znacznie ciekawsza. Przykładowo jeden z ważniejszych wyników tamtego okresu (1983 rok) to dowód, że ciąg funkcji 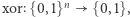 które zwracają sumę wejść modulo dwa, nie może być opisany ciągiem obwodów (dla coraz większej liczby zmiennych) o stałej głębokości, czyli długości najdłuższej ścieżki od wejścia do wyjścia (czyli xor nie należy do klasy
które zwracają sumę wejść modulo dwa, nie może być opisany ciągiem obwodów (dla coraz większej liczby zmiennych) o stałej głębokości, czyli długości najdłuższej ścieżki od wejścia do wyjścia (czyli xor nie należy do klasy 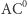 ). Tego typu rezultatów niemożliwości dowodzono wtedy więcej i wierzono, że postęp w tych technikach może doprowadzić do wykazania, że
). Tego typu rezultatów niemożliwości dowodzono wtedy więcej i wierzono, że postęp w tych technikach może doprowadzić do wykazania, że 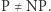 Oczekiwany dowód miałby podążać mniej więcej po następującej linii:
Oczekiwany dowód miałby podążać mniej więcej po następującej linii:
- 1)
- definiujemy jakąś sprytną miarę skomplikowania funkcji boolowskiej,
- 2)
- wykazujemy, że miara funkcji SAT (czyli przypisującej kodowaniom zero-jedynkowym spełnialnych formuł jedynkę, a reszcie zero) lub jakiejś innej funkcji z klasy
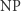 jest duża,
jest duża, - 3)
- pokazujemy, że wszystkie obwody wielomianowej wielkości opisują funkcje o małej mierze.
Ponieważ wiemy, że każdą funkcję z 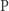 można zapisać wielomianowym obwodem (w takim obwodzie można zakodować algorytm wielomianowy, który jest wykonywany przez bramki), to powyższe punkty pokazywałyby, że
można zapisać wielomianowym obwodem (w takim obwodzie można zakodować algorytm wielomianowy, który jest wykonywany przez bramki), to powyższe punkty pokazywałyby, że 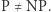
Niestety, (a może raczej na szczęście) i tu pojawiła się nieoczekiwana trudność. W roku 1994 Razborov i Rudich przedstawili swoją pracę na temat "dowodów naturalnych", w której pokazywali, że takiej miary nie można zdefiniować, o ile tylko prawdziwa jest powszechnie uznawana za prawdziwą hipoteza na temat istnienia pseudolosowych funkcji. Główne idee ich dowodu, mimo, że przełomowego i bardzo pomysłowego, dadzą się pokrótce naszkicować. Autorzy pokazali też, że wszystkie wcześniejsze dowody różności klas złożoności korzystały z pewnych własności funkcji, które to własności nazwali naturalnymi. Powiemy, że własność  funkcji jest naturalna, jeśli spełnia trzy warunki:
funkcji jest naturalna, jeśli spełnia trzy warunki:
- i)
- co najmniej
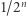 funkcji
funkcji 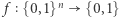 spełnia
spełnia 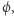
- ii)
- jeśli
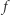 spełnia
spełnia 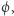 to nie ma obwodu wielomianowej wielkości, który ją opisuje,
to nie ma obwodu wielomianowej wielkości, który ją opisuje, - iii)
- spełnianie
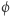 daje się obliczyć w czasie
daje się obliczyć w czasie 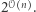
Gwoli ścisłości, definicja naturalności zależy jeszcze od tego, jakie klasy złożoności chcemy rozróżniać, ale my tu skupimy się na powyższej definicji. Gdybyśmy chcieli realizować plan naszkicowany w poprzednim akapicie, to funkcja spełniałaby 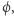 gdyby miała dużą miarę skomplikowania - autorzy przedstawili przekonujące argumenty, że dla każdej rozsądnej miary rzeczywiście spełnione byłyby punkty i), ii), iii). Niemniej jednak, co było głównym wynikiem pracy, o ile tylko istnieją funkcje pseudolosowe, to nie istnieje żadna naturalna własność
gdyby miała dużą miarę skomplikowania - autorzy przedstawili przekonujące argumenty, że dla każdej rozsądnej miary rzeczywiście spełnione byłyby punkty i), ii), iii). Niemniej jednak, co było głównym wynikiem pracy, o ile tylko istnieją funkcje pseudolosowe, to nie istnieje żadna naturalna własność 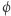 (a więc nie użyjemy jej w dowodzie). Funkcje pseudolosowe to takie, które wyglądają jak losowe z punktu widzenia obserwatora o ograniczonej mocy obliczeniowej. Idea dowodu jest następująca. Weźmy dowolną funkcję, kandydata na funkcję pseudolosową. Losowa funkcja spełnia własność
(a więc nie użyjemy jej w dowodzie). Funkcje pseudolosowe to takie, które wyglądają jak losowe z punktu widzenia obserwatora o ograniczonej mocy obliczeniowej. Idea dowodu jest następująca. Weźmy dowolną funkcję, kandydata na funkcję pseudolosową. Losowa funkcja spełnia własność 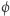 z prawdopodobieństwem co najwyżej
z prawdopodobieństwem co najwyżej 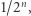 co wynika z i). Natomiast funkcja pseudolosowa musi być prosta w opisie, więc ma obwód wielomianowej wielkości (z ii)), czyli spełnia
co wynika z i). Natomiast funkcja pseudolosowa musi być prosta w opisie, więc ma obwód wielomianowej wielkości (z ii)), czyli spełnia 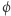 z prawdopodobieństwem
z prawdopodobieństwem 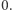 A zatem z prawdopodobieństwem co najmniej
A zatem z prawdopodobieństwem co najmniej 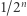 własność
własność 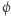 rozróżnia funkcję losową od naszej, a to, czy funkcja spełnia
rozróżnia funkcję losową od naszej, a to, czy funkcja spełnia 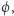 można obliczyć w czasie
można obliczyć w czasie 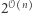 (z iii)). Więc nasza funkcja nie jest pseudolosowa, bo można ją odróżnić od losowej z sensownym prawdopodobieństwem i w odpowiednio ograniczonym czasie. Nie ma więc żadnej takiej - sprzeczność z powszechnie uznawaną hipotezą. Razborov i Rudich w 2007 roku otrzymali nagrodę Gödla za ten rezultat, przez wielu uznawany za najważniejszy wynik dotyczący problemu
(z iii)). Więc nasza funkcja nie jest pseudolosowa, bo można ją odróżnić od losowej z sensownym prawdopodobieństwem i w odpowiednio ograniczonym czasie. Nie ma więc żadnej takiej - sprzeczność z powszechnie uznawaną hipotezą. Razborov i Rudich w 2007 roku otrzymali nagrodę Gödla za ten rezultat, przez wielu uznawany za najważniejszy wynik dotyczący problemu 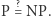
Również i ten wynik istotnie zmienił społeczność informatyków. Ludzie odwrócili się od obwodów logicznych, przestali dowodzić dolne ograniczenia dla nich, bo jak pokazuje powyższy wynik - nie tędy droga. Być może znów zrobiono to zbyt pochopnie, a barierę należy raczej traktować jako drogowskaz, którędy nie iść, tzn. żeby nie definiować naturalnych własności w swoich dowodach. Niedawno zaczęto stosować pewne techniki omijające powyższe bariery i używające algebry. Żeby zrozumieć ideę, przyjrzyjmy się szkicowi dowodu wspomnianego wyżej faktu, że xor nie należy do klasy 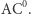 Dowód bada, jak dobrze można przybliżyć funkcję
Dowód bada, jak dobrze można przybliżyć funkcję 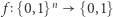 wielomianem wielu zmiennych nad ciałem
wielomianem wielu zmiennych nad ciałem 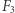 o stopniu co najwyżej
o stopniu co najwyżej 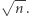 Przez przybliżenie mamy na myśli zwrócenie takiego samego wyniku w większości przypadków. Okazuje się, że każdą funkcję należącą do klasy
Przez przybliżenie mamy na myśli zwrócenie takiego samego wyniku w większości przypadków. Okazuje się, że każdą funkcję należącą do klasy 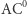 można przybliżyć całkiem nieźle, natomiast funkcji xor nie da się przybliżyć dobrze. Akurat ten dowód nie omija bariery dowodów naturalnych, ale stosując podobne techniki używające wielomianów niskich stopni nad skończonymi ciałami lub pierścieniami, można ominąć obie wspomniane bariery. Ale i ta technika ma ograniczenia; niedawna praca Aaronsona i Widgersona z roku 2009 wprowadza nową barierę zwaną algebraizacją. Jest to uogólnienie relatywizacji. Inkluzja
można przybliżyć całkiem nieźle, natomiast funkcji xor nie da się przybliżyć dobrze. Akurat ten dowód nie omija bariery dowodów naturalnych, ale stosując podobne techniki używające wielomianów niskich stopni nad skończonymi ciałami lub pierścieniami, można ominąć obie wspomniane bariery. Ale i ta technika ma ograniczenia; niedawna praca Aaronsona i Widgersona z roku 2009 wprowadza nową barierę zwaną algebraizacją. Jest to uogólnienie relatywizacji. Inkluzja 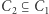 się algebraizuje, jeśli
się algebraizuje, jeśli 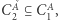 dla pewnej wyroczni
dla pewnej wyroczni 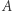 oraz wyroczni
oraz wyroczni 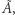 która powstała z
która powstała z 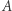 poprzez rozszerzenie z funkcji boolowskich do wielomianów niskich stopni nad skończonym ciałem (dla pierścieni to też działa). Jeśli się algebraizuje, to pewnymi technikami bazującymi na wielomianach niskich stopni (tzw. algebraizującymi się) nie da się jej obalić, podobnie jak fakt, iż
poprzez rozszerzenie z funkcji boolowskich do wielomianów niskich stopni nad skończonym ciałem (dla pierścieni to też działa). Jeśli się algebraizuje, to pewnymi technikami bazującymi na wielomianach niskich stopni (tzw. algebraizującymi się) nie da się jej obalić, podobnie jak fakt, iż 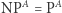 pokazuje, że technikami, które się relatywizują, nie da się obalić inkluzji
pokazuje, że technikami, które się relatywizują, nie da się obalić inkluzji 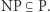 Autorzy wykazali też, że inkluzja
Autorzy wykazali też, że inkluzja 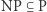 się algebraizuje, czyli techniki, które się algebraizują, nie pozwolą na jej obalenie. Oznacza to, że piłeczka poszukiwaczy dowodu
się algebraizuje, czyli techniki, które się algebraizują, nie pozwolą na jej obalenie. Oznacza to, że piłeczka poszukiwaczy dowodu 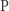
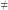
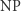 po raz kolejny została odbita.
po raz kolejny została odbita.
Jaka jest przyszłość problemu 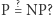 Nie wiadomo. Większość badaczy twierdzi, że
Nie wiadomo. Większość badaczy twierdzi, że 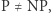 ale są też poważani naukowcy, którzy twierdzą, że wręcz przeciwnie,
ale są też poważani naukowcy, którzy twierdzą, że wręcz przeciwnie, 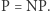 Najprawdopodobniej nieprędko się to wyjaśni, bo, jak widać, nie bez przyczyny problem ten trzyma się długo, kolejne bariery rzucają nam kłody pod nogi. Musimy uzbroić się w cierpliwość. Albo sami ruszyć do starcia z niedostępnym do tej pory problemem. Tylko pamiętajmy, że jeśli zdecydujemy się na to ostatnie, to należy wcześniej mądrze i gruntownie przygotować się do ataku!
Najprawdopodobniej nieprędko się to wyjaśni, bo, jak widać, nie bez przyczyny problem ten trzyma się długo, kolejne bariery rzucają nam kłody pod nogi. Musimy uzbroić się w cierpliwość. Albo sami ruszyć do starcia z niedostępnym do tej pory problemem. Tylko pamiętajmy, że jeśli zdecydujemy się na to ostatnie, to należy wcześniej mądrze i gruntownie przygotować się do ataku!