Informatyczny kącik olimpijski
Palindromiczny podciąg
W tym miesiącu omówimy zadanie Palindromic Subsequence, które pojawiło się na konkursie SRM 708 na platformie Topcoder.
Palindrom to słowo, które nie zmienia się, gdy czytamy je od prawej do lewej, np. "kajak" lub "abba".
W zadaniu dane jest słowo  o długości
o długości 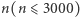 znaków. Dla każdego indeksu
znaków. Dla każdego indeksu 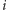 mamy znaleźć liczbę palindromicznych podciągów
mamy znaleźć liczbę palindromicznych podciągów 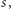 które zawierają
które zawierają 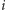 -tą literę
-tą literę 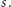 Wyniki należy wypisać modulo
Wyniki należy wypisać modulo 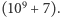
Innymi słowy: dla ustalonego 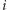 mamy
mamy 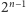 sposobów na usunięcie niektórych z pozostałych
sposobów na usunięcie niektórych z pozostałych 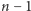 liter w
liter w 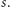 Interesuje nas liczba sposobów, dla których nieusunięte litery utworzą palindrom (
Interesuje nas liczba sposobów, dla których nieusunięte litery utworzą palindrom ( 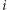 -ta litera jest, oczywiście, nieusunięta).
-ta litera jest, oczywiście, nieusunięta).
Zacznijmy od rozwiązania prostszego zadania - policzmy wszystkie palidromiczne podciągi w danym słowie.
Złym pomysłem jest przetwarzanie słowa od lewej do prawej, bo zapewne musielibyśmy dokładnie pamiętać już wybrany podciąg, by później wybrać te same litery w odwróconej kolejności (by powstał palindrom). Zamiast tego policzymy wynik dla każdego przedziału, zaczynając od przedziałów o długości 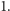
Niech ![|in[i][ j]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/1x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) oznacza liczbę palindromicznych podciągów przedziału
oznacza liczbę palindromicznych podciągów przedziału ![|[i, j]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/2x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) (tzn. palindromicznych podciągów podsłowa złożonego z liter
(tzn. palindromicznych podciągów podsłowa złożonego z liter 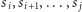 ). Szczegółem implementacyjnym jest decyzja, czy należy liczyć puste podciągi. Zacznijmy analizę od wstępnego wzoru (wcale nieprzypadkowo podobnego do wzoru na liczenie sum prefiksowych w macierzy!):
). Szczegółem implementacyjnym jest decyzja, czy należy liczyć puste podciągi. Zacznijmy analizę od wstępnego wzoru (wcale nieprzypadkowo podobnego do wzoru na liczenie sum prefiksowych w macierzy!):
![in[i][ j] = in[i +1][ j]+ in[i][ j − 1] −in[i +1][ j− 1].](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/4x-ad028b1da444d7ab904265926948720aa358e5f2-dm-33,33,33-FF,FF,FF.gif)
Dodajemy tu liczby palindromicznych podciągów w przedziałach ![|[i +1, j]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/5x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) i
i ![[i, j− 1],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/6x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) po czym odejmujemy te w przedziale
po czym odejmujemy te w przedziale ![[i + 1, j− 1],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/7x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) bo policzyliśmy je podwójnie. Policzyliśmy w ten sposób wszystkie palindromiczne podciągi, które występują też w którymś z krótszych przedziałów. Pozostaje jednak nieuwzględniony przypadek, gdy podciąg zawiera
bo policzyliśmy je podwójnie. Policzyliśmy w ten sposób wszystkie palindromiczne podciągi, które występują też w którymś z krótszych przedziałów. Pozostaje jednak nieuwzględniony przypadek, gdy podciąg zawiera 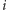 -tą i
-tą i 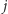 -tą literę - taki podciąg nie występuje ani w
-tą literę - taki podciąg nie występuje ani w ![|[i + 1, j],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/10x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) ani w
ani w ![[i, j− 1].](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/11x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) Skoro
Skoro 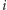 -ta i
-ta i 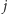 -ta litera są pierwszą i ostatnią literą w przedziale, muszą one być równe, by powstał palindrom. Jeśli tak rzeczywiście jest, to do
-ta litera są pierwszą i ostatnią literą w przedziale, muszą one być równe, by powstał palindrom. Jeśli tak rzeczywiście jest, to do ![in[i][ j]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/14x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) powinniśmy jeszcze dodać
powinniśmy jeszcze dodać ![in[i + 1][ j− 1],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/15x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) bo do każdego z podciągów przedziału
bo do każdego z podciągów przedziału ![[i +1, j− 1]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/16x-ad028b1da444d7ab904265926948720aa358e5f2-im-33,33,33-FF,FF,FF.gif) możemy teraz dodać
możemy teraz dodać 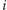 -tą i
-tą i 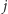 -tą literę z przodu i z tyłu, co da nam nowy dłuższy palindrom.
-tą literę z przodu i z tyłu, co da nam nowy dłuższy palindrom.
Mówimy, że w palindromie pierwsza litera jest sparowana z ostatnią, druga z przedostatnią itd. Zastanówmy się, jak dla pary indeksów 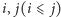 policzyć takie palindromiczne podciągi, które zawierają indeksy
policzyć takie palindromiczne podciągi, które zawierają indeksy 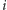 i
i 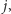 a ponadto w nich te dwie litery są ze sobą sparowane. Musi zatem zachodzić równość
a ponadto w nich te dwie litery są ze sobą sparowane. Musi zatem zachodzić równość 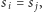 a wzięte indeksy z przedziału
a wzięte indeksy z przedziału ![|[i +1, j −1]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/5x-28510ee4b3a220878ffe3f011ebbf803b241ee3c-im-33,33,33-FF,FF,FF.gif) muszą tworzyć palindromiczny podciąg. Takich podciągów jest dokładnie
muszą tworzyć palindromiczny podciąg. Takich podciągów jest dokładnie ![in[i +1][ j− 1].](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/6x-28510ee4b3a220878ffe3f011ebbf803b241ee3c-im-33,33,33-FF,FF,FF.gif) Pozostaje nam jeszcze uwzględnić liczbę możliwych zewnętrznych rozszerzeń, a więc policzyć liczbę takich wyborów, że litery wzięte na lewo od
Pozostaje nam jeszcze uwzględnić liczbę możliwych zewnętrznych rozszerzeń, a więc policzyć liczbę takich wyborów, że litery wzięte na lewo od 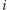 (te z mniejszymi indeksami) odpowiadają literom wziętym na prawo od
(te z mniejszymi indeksami) odpowiadają literom wziętym na prawo od 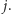 Tę liczbę oznaczmy przez
Tę liczbę oznaczmy przez ![out[i− 1][ j+ 1].](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/9x-28510ee4b3a220878ffe3f011ebbf803b241ee3c-im-33,33,33-FF,FF,FF.gif) Za chwilę pokażemy, jak ją obliczać.
Za chwilę pokażemy, jak ją obliczać.
Niech ![out[i][ j]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/1x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) oznacza liczbę palindromicznych podciągów, które zawierają indeksy z przedziałów
oznacza liczbę palindromicznych podciągów, które zawierają indeksy z przedziałów ![[1,i]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/2x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![[ j,n],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/3x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) a także takich, że litery z
a także takich, że litery z ![|[1,i]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/4x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) są sparowane z tymi z
są sparowane z tymi z ![|[ j,n]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/5x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) (czyli te dwa przedziały zawierają po tyle samo wybranych liter). Podobnie jak do liczenia wartości
(czyli te dwa przedziały zawierają po tyle samo wybranych liter). Podobnie jak do liczenia wartości 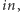 możemy zacząć od rekurencyjnego wzoru:
możemy zacząć od rekurencyjnego wzoru:
![out[i][ j] = out[i −1][ j]+ out[i][ j+ 1] − out[i− 1][ j +1],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/7x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-dm-33,33,33-FF,FF,FF.gif)
po czym dodać ![|out[i− 1][ j +1],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/8x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) jeśli
jeśli 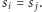 Uwzględniamy tu podciągi, które zawierają indeksy z
Uwzględniamy tu podciągi, które zawierają indeksy z ![[1,i− 1]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/10x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) i
i ![|[ j,n]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/11x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) oraz podciągi, które zawierają indeksy z
oraz podciągi, które zawierają indeksy z ![[1,i]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/12x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) i
i ![|[ j + 1,n].](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/13x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) Do obu tych grup podciągów należą takie, które zawierają indeksy z
Do obu tych grup podciągów należą takie, które zawierają indeksy z ![[1,i− 1]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/14x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) i
i ![[ j+ 1,n],](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/15x-f8fb2ef0f7e585dd3d52d51638bada3d2313719a-im-33,33,33-FF,FF,FF.gif) więc takie policzyliśmy dwukrotnie, co musimy odjąć. Dodatkowo, jeśli litery
więc takie policzyliśmy dwukrotnie, co musimy odjąć. Dodatkowo, jeśli litery 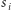 i
i 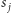 są równe, uwzględniamy podciągi, które je zawierają.
są równe, uwzględniamy podciągi, które je zawierają.
Zauważmy, że w każdym palindromicznym podciągu zawierającym 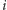 -tą literę, litera ta jest sparowana z dokładnie jedną literą, która musi być, oczywiście, równa
-tą literę, litera ta jest sparowana z dokładnie jedną literą, która musi być, oczywiście, równa 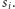 By znaleźć wynik zadania dla
By znaleźć wynik zadania dla 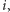 wystarczy więc przeiterować wszystkie indeksy
wystarczy więc przeiterować wszystkie indeksy 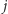 (
( 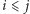 i
i 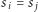 ) i zsumować iloczyny
) i zsumować iloczyny ![|out[i− 1][ j + 1] ⋅in[i + 1][ j− 1]](/math/temat/informatyka/algorytmy/2017/08/27/Palindromiczny_podciag/7x-8b10c163cdb4d1209545cd2d96385246e574be7e-im-33,33,33-FF,FF,FF.gif) (taki iloczyn jest równy liczbie palindromicznych podciągów, w których indeksy
(taki iloczyn jest równy liczbie palindromicznych podciągów, w których indeksy 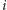 i
i 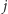 są sparowane).
są sparowane).
Zarówno obliczenie tablic 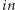 i
i 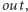 jak i końcowe iterowanie par indeksów, ma złożoność czasową
jak i końcowe iterowanie par indeksów, ma złożoność czasową 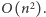 Tablice
Tablice 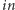 i
i 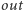 mają rozmiar kwadratowy. Czytelnikowi Z Ograniczoną Pamięcią pozostawiamy zastanowienie się nad implementacją w pamięci liniowej.
mają rozmiar kwadratowy. Czytelnikowi Z Ograniczoną Pamięcią pozostawiamy zastanowienie się nad implementacją w pamięci liniowej.