Problem Stopu

Tak zwany Problem Stopu to problem decyzyjny, którego wejściem jest jakiś program 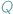$Q$ i jakieś dane 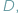$D;$ a którego rozwiązaniem (wyjściem) jest stwierdzenie, czy program 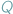$Q$ uruchomiony na danych 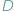$D$ zakończy swoje działania w skończonym czasie.

Twierdzenie. Problem Stopu jest nierozstrzygalny.

Dowód. Załóżmy nie wprost, że Problem Stopu jest rozstrzygalny, a więc, że istnieje program P(Q, D), który zawsze (a więc w skończonym czasie dla każdych danych) rozstrzyga Problem Stopu. Rozważmy teraz następujący program P', którego wejściem jest jakiś inny program X:

$boolean P ’ (program X ) { if (P(X, X)) { while (true ) do {}; } //wymuszamy pętlenie się else { return true; } }$

Będziemy się zastanawiać, czy wykonanie P'(P') zatrzyma się, czy nie.

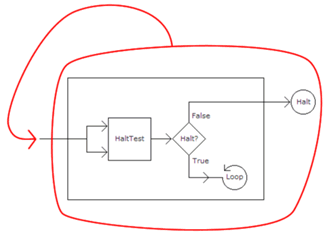
Najpierw załóżmy, że się zatrzyma. Wtedy oczywiście (z definicji P)
P(P', P') zwraca true. Jednak wówczas z kodu programu P' (spójrzmy na warunek po if) wynika, że P'(P') się pętli w nieskończoność. Sprzeczność.

Z drugiej strony: załóżmy, że P'(P') się nie zatrzyma. To jednak (znów analizujemy kod P') implikuje, że P(P', P') zwraca true, ale to przecież oznacza, że P'(P') się zatrzymuje. Ponownie uzyskaliśmy sprzeczność, co kończy dowód.