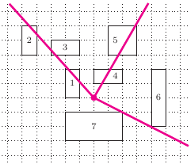
Rys. 1 W mieście znajduje się siedem budynków. Aby zniszczyć je wszystkie, wystarczy, że kosmita użyje działa trzy razy.

Zgodnie z treścią zadania tym razem nie będziemy ratowali świata, ale mamy pomóc kosmicie, który wylądowawszy w centrum miasta swoim statkiem, chce siać totalne zniszczenie. W tym celu użyje on potężnego działa laserowego, którego promień jest w stanie zniszczyć wszystko, co znajdzie się na jego drodze. Do nas należy wyznaczenie minimalnej liczby strzałów potrzebnej do zniszczenia wszystkich budynków w mieście. Każdy budynek możemy utożsamić z pewnym prostokątem o bokach równoległych do osi prostokątnego układu współrzędnych; wystarczy, że promień lasera dotknie dowolnego punktu takiego prostokąta (Rys. 1).

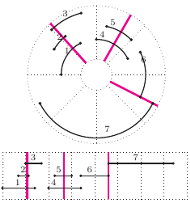
Rys 2. Zbiór przedziałów na okręgu odpowiadających budynkom z rysunku 1 oraz ten sam zbiór na odcinku po rozcięciu okręgu. Przedziały w kolejności rozpatrywania przez algorytm zachłanny to 2, 1, 3, 5, 4, 6, 7; algorytm strzeli w końce przedziałów 2, 5 i 6.

Zauważmy, że zbiór promieni, które mogą zniszczyć ustalony budynek, tworzy pewien kąt. Aby go wyznaczyć, wystarczy rozpatrzeć cztery promienie przechodzące przez wierzchołki prostokąta odpowiadającego budynkowi. Co więcej, konkretny kształt i położenie budynku nie jest istotne - wystarczy nam jedynie znajomość wspomnianego kąta.

Zatem pierwsze, co zrobimy, to zamienimy geometryczny problem na płaszczyźnie dwuwymiarowej na równoważny problem jednowymiarowy na okręgu (Rys. 2). W tym problemie mamy dane przedziałów na okręgu (odpowiadających kątom dla budynków). Należy znaleźć minimalną liczbę półprostych wychodzących ze środka okręgu ( "strzałów"), tak by każdy przedział był przecięty co najmniej jedną półprostą.

Na rozgrzewkę rozwiążemy prostszą wersję tego problemu. Jeżeli istnieje półprosta wychodząca ze środka okręgu i nieprzecinająca żadnego z przedziałów, to możemy rozciąć okrąg wzdłuż tej półprostej i rozwiązać zadanie na odcinku. Nietrudno się przekonać, że działa wtedy następujące rozwiązanie zachłanne. Sortujemy przedziały niemalejąco po prawych końcach, a następnie przeglądamy je w tej właśnie kolejności. Za każdym razem, gdy natrafiamy na przedział, w który jeszcze nie strzelaliśmy (tzn. którego początek znajduje się za ostatnim strzałem), musimy wykonać nowy strzał; opłaca nam się to zrobić jak najdalej, czyli na końcu tego przedziału. Takie rozwiązanie będzie działać w czasie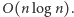

Spróbujmy uogólnić ten pomysł w przypadku, gdy nie mamy dobrego kandydata na rozcięcie okręgu. Zauważmy, że i w tym przypadku istnieje rozwiązanie optymalne, w którym strzelamy jedynie w końce przedziałów. Istotnie: każdy strzał przecinający pewien zbiór przedziałów można przesunąć na koniec tego przedziału ze zbioru, który kończy się najwcześniej. Dostajemy zatem rozwiązanie o złożoności czasowej 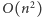: dla każdego z przedziałów sprawdzamy, ile strzałów musimy zużyć, jeśli strzelimy w koniec tego przedziału (rozcinając tym samym okrąg), a w pozostałe przedziały strzelając zgodnie z algorytmem zachłannym.

Niech będzie optymalną liczbą strzałów. Z powyższych rozważań wynika, że koniec danego przedziału albo należy do pewnego optymalnego rozwiązania, albo, strzelając w niego, uzyskamy rozwiązanie o liczbie strzałów 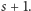Kluczowe jest teraz znalezienie co najmniej jednego "optymalnego" przedziału.

W tym celu zdefiniujmy tablicę która dla przedziału 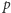oznacza przedział o najwcześniejszym końcu spośród przedziałów, których początek leży za końcem przedziału 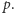Mając przedziały posortowane po końcach, tablicę 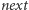można wyznaczyć w czasie 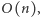poruszając się po okręgu dwoma wskaźnikami. Zauważmy, że jeśli zaczynamy od przedziału 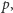to zgodnie z rozwiązaniem zachłannym będziemy strzelać w przedziały aż obejdziemy cały okrąg.

I teraz kluczowa obserwacja: zaczynając z dowolnego przedziału 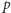i wykonując 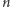razy przypisanie zawsze wylądujemy w pewnym przedziale optymalnym. Dowód jest nieco techniczny i wymaga przyjrzenia się, jak wyglądałaby sytuacja, gdyby wszystkie przedziały były nieoptymalne; zostawiamy go jako ćwiczenie dla Czytelnika.

Ostatecznie algorytm ma złożoność czasową 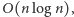zdominowaną przez sortowanie przedziałów. Pozostałe fazy (wyznaczenie przedziałów dla prostokątów, wyznaczenie tablicy 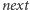i pewnego przedziału optymalnego, algorytm zachłanny) działają w czasie liniowym.