Informatyczny kącik olimpijski
Flagi

W tym miesiącu, chcąc polecić Czytelnikom kącika książkę Zaprzyjaźnij się z algorytmami, przedstawimy jedno zadanie z tej pozycji. Wybieramy się na wyprawę w góry.
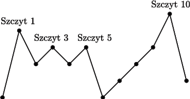
Rys. 1
Zadanie. Na mapie trasy zaznaczyliśmy  kolejnych miejsc o wysokościach
kolejnych miejsc o wysokościach 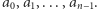 Podczas wędrówki chcemy rozmieścić jak największą liczbę flag na szczytach, czyli takich miejscach, dla których dwa sąsiednie miejsca są położone niżej (zakładamy, że pierwsze i ostatnie miejsce nie są szczytami). Jest jedno ograniczenie: jeśli rozmieszczamy
Podczas wędrówki chcemy rozmieścić jak największą liczbę flag na szczytach, czyli takich miejscach, dla których dwa sąsiednie miejsca są położone niżej (zakładamy, że pierwsze i ostatnie miejsce nie są szczytami). Jest jedno ograniczenie: jeśli rozmieszczamy 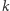 flag, to odległość pomiędzy dwiema dowolnymi flagami powinna być równa co najmniej
flag, to odległość pomiędzy dwiema dowolnymi flagami powinna być równa co najmniej 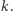
Przykładowo dla trasy opisanej tablicą ![a = [1,5,3,4,3,4,1,2,3,4,6,2]](/math/temat/informatyka/algorytmy/2016/08/31/Flagi/1x-c4a6698156e17c9a06f5beda79d3cf5bfc986fcc-im-33,33,33-FF,FF,FF.gif) mamy dokładnie cztery szczyty (Rys. 1]).
mamy dokładnie cztery szczyty (Rys. 1]).
Na tej trasie możemy rozmieścić 3 flagi (np. na szczytach 1, 5 i 10). Nie możemy jednak rozmieścić 4 flag, tak aby odległość pomiędzy nimi była równa co najmniej 4.
Wynik może być znaleziony przy użyciu wyszukiwania binarnego. Jeśli wiemy, że 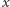 flag może zostać rozmieszczonych na szczytach, to również wiemy, że każda ich mniejsza liczba może też być rozmieszczona. Z drugiej strony, jeśli
flag może zostać rozmieszczonych na szczytach, to również wiemy, że każda ich mniejsza liczba może też być rozmieszczona. Z drugiej strony, jeśli  flag nie może zostać rozmieszczonych, to każda większa liczba flag również nie może być rozmieszczona. W ten sposób, używając wyszukiwania binarnego, redukujemy problem do sprawdzenia, czy można rozmieścić na szczytach ustaloną liczbę
flag nie może zostać rozmieszczonych, to każda większa liczba flag również nie może być rozmieszczona. W ten sposób, używając wyszukiwania binarnego, redukujemy problem do sprawdzenia, czy można rozmieścić na szczytach ustaloną liczbę 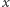 flag. Taki problem możemy rozwiązać już zachłannie: idziemy trasą i zawsze ustawiamy flagę na najbliższym dozwolonym szczycie. Całe rozwiązanie działa w czasie
flag. Taki problem możemy rozwiązać już zachłannie: idziemy trasą i zawsze ustawiamy flagę na najbliższym dozwolonym szczycie. Całe rozwiązanie działa w czasie 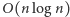 ze względu na czas wyszukiwania binarnego.
ze względu na czas wyszukiwania binarnego.
Zadanie da się rozwiązać szybciej, w czasie liniowym. Na początku, dla każdego miejsca, jeśli nie jest szczytem, znajdujemy najbliższy szczyt położony na dalszym odcinku trasy. W tym celu możemy najpierw oznaczyć wszystkie szczyty, a następnie przeglądać trasę w odwróconej kolejności, pamiętając pozycję ostatnio spotkanego szczytu. W ten sposób wypełnimy tablicę 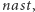 gdzie
gdzie ![|nast[i]](/math/temat/informatyka/algorytmy/2016/08/31/Flagi/2x-6f7e7ec5f1f94f8c6ef2e91cbbefb36cef2d8f87-im-33,33,33-FF,FF,FF.gif) będzie najbliższym szczytem od miejsca numer
będzie najbliższym szczytem od miejsca numer 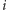 na prawo (lub wartość
na prawo (lub wartość 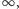 jeżeli dalej nie występuje już żaden szczyt). Dla powyższego rysunku mamy
jeżeli dalej nie występuje już żaden szczyt). Dla powyższego rysunku mamy ![nast = [1,1,3,3,5,5,10,10,10,10,10,∞ ].](/math/temat/informatyka/algorytmy/2016/08/31/Flagi/5x-6f7e7ec5f1f94f8c6ef2e91cbbefb36cef2d8f87-im-33,33,33-FF,FF,FF.gif)
Zauważmy, że możemy rozmieścić co najwyżej 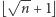 flag. Ta obserwacja doprowadzi nas do rozwiązania optymalnego. Jeśli ustawiamy jakąś flagę na pozycji
flag. Ta obserwacja doprowadzi nas do rozwiązania optymalnego. Jeśli ustawiamy jakąś flagę na pozycji 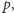 to wiemy, że następna flaga powinna być ustawiona na pozycji dalszej lub równej
to wiemy, że następna flaga powinna być ustawiona na pozycji dalszej lub równej 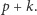 Takie miejsce możemy znaleźć w czasie stałym, korzystając z tablicy
Takie miejsce możemy znaleźć w czasie stałym, korzystając z tablicy 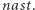 Pseudokod takiego rozwiązania może wyglądać następująco:
Pseudokod takiego rozwiązania może wyglądać następująco:
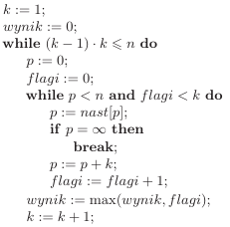
Całkowita liczba operacji nie przekroczy 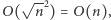 gdyż zarówno zewnętrzna jak i wewnętrzna pętla zostaną wykonane co najwyżej
gdyż zarówno zewnętrzna jak i wewnętrzna pętla zostaną wykonane co najwyżej 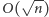 razy.
razy.