Informatyczny kącik olimpijski
Myszy
Tym razem zajmiemy się zadaniem, które pojawiło się na kolokwium dla studentów pierwszego roku informatyki na Uniwersytecie Warszawskim.
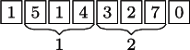
Dla 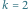 oraz tablicy
oraz tablicy

poprawnym wynikiem jest 14. Jeden kot może pilnować fragmentu korytarza na metrach od 2 do 4 (łapiąc 6 z 10 myszy), a drugi może pilnować fragmentu na metrach od 5 do 7 (łapiąc 8 z 12 myszy).
W korytarzu harcują myszy. Korytarz ma długość 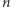 metrów. Dana jest tablica
metrów. Dana jest tablica  nieujemnych liczb całkowitych
nieujemnych liczb całkowitych ![a[]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/3x-78c922f9e3e28bf1a4c9574c90063e7f3d87ca8f-im-33,33,33-FF,FF,FF.gif) opisująca, gdzie jest ile myszy: dla
opisująca, gdzie jest ile myszy: dla 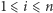 na
na 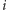 -tym metrze korytarza (patrząc od strony wejścia) jest
-tym metrze korytarza (patrząc od strony wejścia) jest ![a[i]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/6x-78c922f9e3e28bf1a4c9574c90063e7f3d87ca8f-im-33,33,33-FF,FF,FF.gif) myszy. Dysponujesz
myszy. Dysponujesz 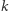 kotami
kotami 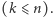 Twoim zadaniem jest takie rozmieszczenie kotów w korytarzu, żeby złapały jak najwięcej myszy. Każdy kot może pilnować ustalonego przez Ciebie spójnego fragmentu korytarza (na przykład, może mieć założoną smycz odpowiedniej długości, przymocowaną do podłogi pośrodku pilnowanego fragmentu korytarza). Fragmenty korytarza pilnowane przez różne koty nie mogą zachodzić na siebie (żeby koty się nie pobiły, a smycze nie poplątały), choć mogą się stykać. Niektóre fragmenty korytarza mogą pozostać niepilnowane przez żadnego kota. Kot, który pilnuje fragmentu od
Twoim zadaniem jest takie rozmieszczenie kotów w korytarzu, żeby złapały jak najwięcej myszy. Każdy kot może pilnować ustalonego przez Ciebie spójnego fragmentu korytarza (na przykład, może mieć założoną smycz odpowiedniej długości, przymocowaną do podłogi pośrodku pilnowanego fragmentu korytarza). Fragmenty korytarza pilnowane przez różne koty nie mogą zachodzić na siebie (żeby koty się nie pobiły, a smycze nie poplątały), choć mogą się stykać. Niektóre fragmenty korytarza mogą pozostać niepilnowane przez żadnego kota. Kot, który pilnuje fragmentu od 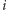 -tego do
-tego do 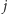 -tego metra włącznie (dla
-tego metra włącznie (dla 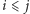 ), na którym znajduje się
), na którym znajduje się ![|s = a[i]+ a[i + 1]+ ⋯ + a[ j]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/12x-78c922f9e3e28bf1a4c9574c90063e7f3d87ca8f-im-33,33,33-FF,FF,FF.gif) myszy, złapie:
myszy, złapie: 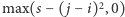 myszy. Należy wyznaczyć maksymalną liczbę myszy, jakie mogą złapać koty (patrz rysunek).
myszy. Należy wyznaczyć maksymalną liczbę myszy, jakie mogą złapać koty (patrz rysunek).
Obojętnie, jak zabierzemy się za to zadanie, przyda się nam tablica sum prefiksowych: ![s[ j] = P1DiD ja[i].](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/1x-39f309bf1a17f37cdd6129d368273694051952e5-im-33,33,33-FF,FF,FF.gif) Wtedy liczba myszy na fragmencie
Wtedy liczba myszy na fragmencie ![|[i, j]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/2x-39f309bf1a17f37cdd6129d368273694051952e5-im-33,33,33-FF,FF,FF.gif) przedstawia się jako
przedstawia się jako ![s[ j]− s[i− 1].](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/3x-39f309bf1a17f37cdd6129d368273694051952e5-im-33,33,33-FF,FF,FF.gif)
Omawiane zadanie to zadanie na programowanie dynamiczne. Niech ![d[ j,l]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/1x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) oznacza maksymalną liczbę myszy, jakie może złapać
oznacza maksymalną liczbę myszy, jakie może złapać 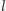 kotów na pierwszych
kotów na pierwszych 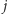 metrach korytarza. Ponieważ niektóre fragmenty mogą być niepilnowane, więc rekurencję budujemy, rozpatrując dwa przypadki: albo
metrach korytarza. Ponieważ niektóre fragmenty mogą być niepilnowane, więc rekurencję budujemy, rozpatrując dwa przypadki: albo 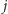 -ty metr nie jest pilnowany, albo jest i
-ty metr nie jest pilnowany, albo jest i 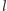 -ty kot pilnuje fragmentu
-ty kot pilnuje fragmentu ![[i, j]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/6x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) (od
(od 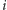 -tego do
-tego do 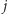 -tego metra włącznie):
-tego metra włącznie):
![d[ j,l] = max (d[ j −1,l],max0DiD j(d[i− 1,l− 1]+ s[ j]− s[i −1]− ( j −i)2)).](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/9x-fcf9011c6ded7741d49b9a75c7076e836c43249c-dm-33,33,33-FF,FF,FF.gif) |
(*) |
Podstawowa implementacja zadziała w czasie 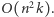 Takie było oczekiwane rozwiązanie na kolokwium, niemniej jednak okazało się, że można to zrobić lepiej (ach, ci studenci). Aby przyspieszyć rozwiązanie, należy w odpowiedniej kolejności wypełniać tablicę
Takie było oczekiwane rozwiązanie na kolokwium, niemniej jednak okazało się, że można to zrobić lepiej (ach, ci studenci). Aby przyspieszyć rozwiązanie, należy w odpowiedniej kolejności wypełniać tablicę 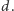 Główna pętla powinna przebiegać po
Główna pętla powinna przebiegać po 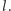 Ustalmy
Ustalmy 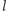 i załóżmy, że mamy obliczone wartości
i załóżmy, że mamy obliczone wartości ![|d[ j,l− 1]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/14x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) dla wszystkich
dla wszystkich 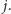 Będziemy teraz obliczać element
Będziemy teraz obliczać element ![d[ j,l].](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/16x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) Kluczem do usprawnienia rozwiązania jest porównanie możliwych dwóch ustawień
Kluczem do usprawnienia rozwiązania jest porównanie możliwych dwóch ustawień 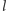 -tego kota, mianowicie gdy patroluje on fragment
-tego kota, mianowicie gdy patroluje on fragment ![[i1, j]](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/18x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) lub fragment
lub fragment ![|[i2, j],](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/19x-fcf9011c6ded7741d49b9a75c7076e836c43249c-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 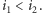 Drugie ustawienie jest lepsze od pierwszego, jeśli:
Drugie ustawienie jest lepsze od pierwszego, jeśli:
![2 2 d[i1−1,l−1]+s[ j]−s[i1− 1]− ( j− i1) < d[i2−1,l−1]+s[ j]−s[i2− 1]− ( j−i2).](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/21x-fcf9011c6ded7741d49b9a75c7076e836c43249c-dm-33,33,33-FF,FF,FF.gif) |
Po przekształceniu nierówność przyjmie postać:
![1 j > (d[i1− 1,l− 1] −d[i2 −1,l− 1]− s[i1−1] +s[i2− 1]− i12+ i22)⋅-------. 2(i2− i1)](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/1x-4dcd12b71cc8ae3f8117ef6b77ff7ab0ebf31492-dm-33,33,33-FF,FF,FF.gif) |
(**) |
Prawa strona nierówności 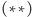 zależy tylko od
zależy tylko od 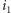 i
i 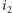 (oraz od
(oraz od 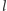 ); oznaczmy ją przez
); oznaczmy ją przez 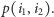 Widzimy, że pierwsze ustawienie jest lepsze dla
Widzimy, że pierwsze ustawienie jest lepsze dla 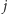 mniejszych od
mniejszych od 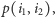 po czym, począwszy od
po czym, począwszy od 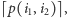 lepsze staje się drugie ustawienie. Ta obserwacja umożliwia przeglądanie możliwych ustawień
lepsze staje się drugie ustawienie. Ta obserwacja umożliwia przeglądanie możliwych ustawień 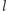 -tego kota w sposób bardziej uporządkowany tak, że na bieżąco eliminujemy takie ustawienia, które są już od pewnych
-tego kota w sposób bardziej uporządkowany tak, że na bieżąco eliminujemy takie ustawienia, które są już od pewnych  gorsze. Trzymamy kolejkę dwukierunkową początków fragmentów
gorsze. Trzymamy kolejkę dwukierunkową początków fragmentów 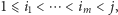 taką że
taką że
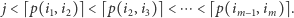 |
Innymi słowy, dla odpowiednio małych 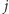 najlepiej przydzielać
najlepiej przydzielać 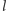 -temu kotu fragment
-temu kotu fragment ![[i1, j],](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/16x-4dcd12b71cc8ae3f8117ef6b77ff7ab0ebf31492-im-33,33,33-FF,FF,FF.gif) gdy
gdy 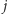 osiągnie
osiągnie 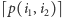 - fragment
- fragment ![[i2, j],](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/19x-4dcd12b71cc8ae3f8117ef6b77ff7ab0ebf31492-im-33,33,33-FF,FF,FF.gif) i tak dalej aż do
i tak dalej aż do 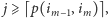 gdzie optymalny przydział to
gdzie optymalny przydział to ![[i , j]. m](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/21x-4dcd12b71cc8ae3f8117ef6b77ff7ab0ebf31492-im-33,33,33-FF,FF,FF.gif) Przetwarzanie
Przetwarzanie 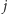 -tego metra korytarza składa się z następujących kroków:
-tego metra korytarza składa się z następujących kroków:
- 1.
- Jeżeli kolejka ma co najmniej dwa elementy oraz
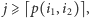 to usuwamy z przodu kolejki
to usuwamy z przodu kolejki 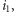 gdyż od tego momentu lepsze będą fragmenty o początku
gdyż od tego momentu lepsze będą fragmenty o początku 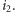
- 2.
- Jeżeli kolejka ma wciąż co najmniej dwa elementy, to sprawdzamy, czy
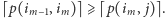 Jeżeli tak, to fragmenty o początku
Jeżeli tak, to fragmenty o początku 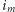 są zdominowane przez fragmenty o początkach
są zdominowane przez fragmenty o początkach 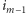 lub
lub 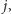 usuwamy więc
usuwamy więc 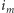 z końca kolejki i powtarzamy krok 2.
z końca kolejki i powtarzamy krok 2. - 3.
- Dodajemy
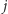 na koniec kolejki.
na koniec kolejki. - 4.
- Obliczamy
![d[j, l],](/math/temat/informatyka/algorytmy/2016/05/25/Myszy/32x-4dcd12b71cc8ae3f8117ef6b77ff7ab0ebf31492-im-33,33,33-FF,FF,FF.gif) korzystając ze wzoru
korzystając ze wzoru 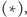 ale możemy to już teraz zrobić w czasie
ale możemy to już teraz zrobić w czasie 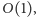 gdyż wiemy, że maksimum jest osiągane przy
gdyż wiemy, że maksimum jest osiągane przy 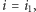 gdzie
gdzie 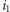 jest aktualnym elementem z przodu kolejki.
jest aktualnym elementem z przodu kolejki.
W ten sposób otrzymaliśmy rozwiązanie o złożoności czasowej 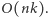
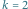 oraz tablicy
oraz tablicy