Informatyczny kącik olimpijski
Wieża z siana
W tym miesiącu zadanie Tower of Hay, które pojawiło się na konkursie USACO Open Gold w roku 2009.
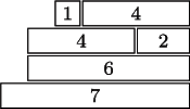
Rys. 1 Dla 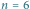 beli o kolejnych szerokościach 7, 6, 4, 2, 1, 4 można zbudować wieżę o wysokości 4
beli o kolejnych szerokościach 7, 6, 4, 2, 1, 4 można zbudować wieżę o wysokości 4
Zadanie. Z 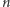 prostopadłościennych beli siana, które mają tę samą wysokość, ale różne szerokości
prostopadłościennych beli siana, które mają tę samą wysokość, ale różne szerokości 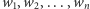 chcemy zbudować wielopoziomową wieżę. Na każdy poziom może się składać kilka beli, a sumaryczna szerokość każdego poziomu musi być nie większa niż sumaryczna szerokość poziomu znajdującego się bezpośrednio pod nim (o ile taki istnieje). Co więcej, żadna bela nie może znajdować się na wyższym poziomie niż inna bela o wyższym numerze (czyli należy je układać po kolei) i należy wykorzystać wszystkie bele. Jaka jest największa możliwa wysokość wieży, którą można zbudować przy takich założeniach (patrz Rys. 1)?
chcemy zbudować wielopoziomową wieżę. Na każdy poziom może się składać kilka beli, a sumaryczna szerokość każdego poziomu musi być nie większa niż sumaryczna szerokość poziomu znajdującego się bezpośrednio pod nim (o ile taki istnieje). Co więcej, żadna bela nie może znajdować się na wyższym poziomie niż inna bela o wyższym numerze (czyli należy je układać po kolei) i należy wykorzystać wszystkie bele. Jaka jest największa możliwa wysokość wieży, którą można zbudować przy takich założeniach (patrz Rys. 1)?
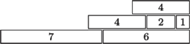
Rys. 2 Algorytm zachłanny dla beli z rysunku 1 zbuduje wieżę o wysokości 3
Dość naturalnym rozwiązaniem zachłannym, które może się nam narzucić, jest konstruowanie każdego poziomu z jak najmniejszej liczby beli siana, podczas budowania wieży od góry. Niestety, jest to rozwiązanie niepoprawne, jak można się przekonać, patrząc na rysunek 2.
Spróbujmy więc rozwiązania opartego o metodę programowania dynamicznego. Niech ![|d[i, j]](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/1x-c24aad8f94fcb086d852eb9587aef891bbceed23-im-33,33,33-FF,FF,FF.gif) oznacza maksymalną wysokość wieży złożonej z beli o szerokościach
oznacza maksymalną wysokość wieży złożonej z beli o szerokościach 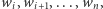 jeśli dolny poziom wieży składa się z beli o szerokościach
jeśli dolny poziom wieży składa się z beli o szerokościach 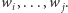 Wtedy mamy następującą rekurencję, w której iterujemy po wszystkich możliwościach zbudowania drugiego poziomu (przyjmujemy tu oznaczenie
Wtedy mamy następującą rekurencję, w której iterujemy po wszystkich możliwościach zbudowania drugiego poziomu (przyjmujemy tu oznaczenie 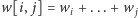 ):
):
![d[i, j] = maxj @kDn{1+ d[ j+ 1,k] w[i,](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/5x-c24aad8f94fcb086d852eb9587aef891bbceed23-dm-33,33,33-FF,FF,FF.gif) |
Czas wypełniania tablicy 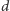 to
to 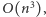 a odpowiedź to
a odpowiedź to ![max1DjDn | d[1, j].](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/8x-c24aad8f94fcb086d852eb9587aef891bbceed23-im-33,33,33-FF,FF,FF.gif)
Można nieco zmodyfikować powyższy pomysł, aby uzyskać rozwiązanie o złożoności czasowej 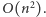 Oznaczmy przez
Oznaczmy przez ![d2[i, | j]](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/2x-f673a2c454ffada3ce003bcab2126e328668470a-im-33,33,33-FF,FF,FF.gif) maksymalną wysokość wieży złożonej z beli
maksymalną wysokość wieży złożonej z beli 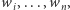 w której dolny poziom nie zawiera beli
w której dolny poziom nie zawiera beli 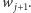 Rekurencja przybierze postać
Rekurencja przybierze postać
![d2[i, j] = max(d2[i, j− 1],1+ d2[ j+ 1,ki, j]),](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/5x-f673a2c454ffada3ce003bcab2126e328668470a-dm-33,33,33-FF,FF,FF.gif) |
gdzie 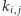 jest maksymalnym indeksem, dla którego
jest maksymalnym indeksem, dla którego 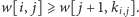 Taki indeks możemy obliczać na bieżąco, jeśli ustalimy indeks
Taki indeks możemy obliczać na bieżąco, jeśli ustalimy indeks 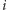 i będziemy wypełniać tablicę
i będziemy wypełniać tablicę  kolejno dla rosnących wartości indeksu
kolejno dla rosnących wartości indeksu 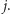 Odpowiedź to
Odpowiedź to ![|d2[1,n].](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/11x-f673a2c454ffada3ce003bcab2126e328668470a-im-33,33,33-FF,FF,FF.gif)

Jeszcze lepsze rozwiązanie uzyskamy, korzystając z obserwacji, że najwyższa wieża będzie miała też najmniejszą szerokość dolnego poziomu. Udowodnijmy to przez indukcję: pokażemy to dla wieży zbudowanej z beli 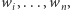 przy założeniu, że teza jest spełniona dla wież zbudowanych z beli o szerokościach
przy założeniu, że teza jest spełniona dla wież zbudowanych z beli o szerokościach 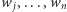 dla
dla 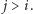 Załóżmy, że wieża o najmniejszej szerokości dolnego poziomu ma go zbudowanego z beli
Załóżmy, że wieża o najmniejszej szerokości dolnego poziomu ma go zbudowanego z beli 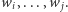 Wtedy najwęższa wieża z beli
Wtedy najwęższa wieża z beli 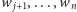 będzie miała (na mocy założenia indukcyjnego) największą wysokość
będzie miała (na mocy założenia indukcyjnego) największą wysokość 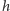 (a zatem cała wieża wysokość
(a zatem cała wieża wysokość 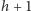 ). Teraz dowolna inna wieża mająca dolny poziom
). Teraz dowolna inna wieża mająca dolny poziom 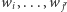 dla
dla 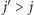 ma resztę zbudowaną z
ma resztę zbudowaną z 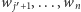 o wysokości
o wysokości 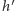 (zatem cała wieża ma wysokość
(zatem cała wieża ma wysokość 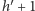 ). Ale wtedy istnieje wieża złożona z
). Ale wtedy istnieje wieża złożona z 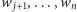 o wysokości
o wysokości 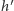 (bo wystarczy rozszerzyć dolny poziom), zatem
(bo wystarczy rozszerzyć dolny poziom), zatem 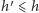 (z maksymalności
(z maksymalności 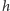 ). To kończy dowód.
). To kończy dowód.
Niech zatem ![d3[i]](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/1x-74ae9ea6a39347bd8951947a5703a7870e86f5b7-im-33,33,33-FF,FF,FF.gif) oznacza taki indeks
oznacza taki indeks 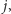 że najwęższa wieża zbudowana z beli o szerokościach
że najwęższa wieża zbudowana z beli o szerokościach 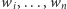 ma dolny poziom złożony z beli o szerokościach
ma dolny poziom złożony z beli o szerokościach 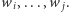 Wtedy mamy rekurencję:
Wtedy mamy rekurencję:
![d3[i] = miniDj Dn{ j w[i,](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/5x-74ae9ea6a39347bd8951947a5703a7870e86f5b7-dm-33,33,33-FF,FF,FF.gif) |
Wyznaczywszy tablicę 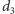 w czasie
w czasie 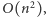 odpowiedź odzyskujemy, obliczając długość ciągu
odpowiedź odzyskujemy, obliczając długość ciągu ![|d [1],d [d [1]+ 1],... 3 3 3](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/8x-74ae9ea6a39347bd8951947a5703a7870e86f5b7-im-33,33,33-FF,FF,FF.gif) zawierającego końce kolejnych poziomów w najwęższej wieży.
zawierającego końce kolejnych poziomów w najwęższej wieży.
Tablicę 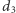 można wypełnić szybciej. Ustalmy indeks
można wypełnić szybciej. Ustalmy indeks 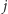 i niech
i niech 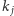 będzie maksymalnym indeksem, dla którego spełniona jest nierówność
będzie maksymalnym indeksem, dla którego spełniona jest nierówność 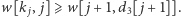 Wiemy zatem, że
Wiemy zatem, że ![d3[i]⩽ j](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/5x-e6be392a5e64f79c503e9acad3f651236cbabe56-im-33,33,33-FF,FF,FF.gif) dla wszystkich
dla wszystkich 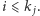 Algorytm jest następujący: dla kolejnych indeksów
Algorytm jest następujący: dla kolejnych indeksów 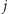 wykonujemy przypisanie
wykonujemy przypisanie ![|d [ j] = min(d [ j],d [ j + 1]), 3 3 3](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/8x-e6be392a5e64f79c503e9acad3f651236cbabe56-im-33,33,33-FF,FF,FF.gif) wyznaczamy wyszukiwaniem binarnym indeks
wyznaczamy wyszukiwaniem binarnym indeks 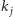 i wykonujemy
i wykonujemy ![d3[kj ] = j.](/math/temat/informatyka/algorytmy/2016/04/28/Wieza_z_siana/10x-e6be392a5e64f79c503e9acad3f651236cbabe56-im-33,33,33-FF,FF,FF.gif) Złożoność czasowa tego algorytmu to
Złożoność czasowa tego algorytmu to 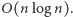
A Czytelników Dociekliwych zachęcamy do rozwiązania tego zadania w optymalnej złożoności czasowej 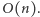
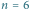 beli o kolejnych szerokościach 7, 6, 4, 2, 1, 4 można zbudować wieżę o wysokości 4
beli o kolejnych szerokościach 7, 6, 4, 2, 1, 4 można zbudować wieżę o wysokości 4