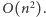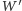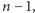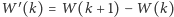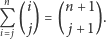Informatyczny kącik olimpijski
Wielomian
W tym miesiącu omówię zadanie Wielomian, które pojawiło się na finale Potyczek Algorytmicznych w 2005 roku.
Zadanie 1. Dany jest wielomian 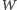 stopnia (co najwyżej)
stopnia (co najwyżej) 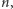 zdefiniowany poprzez jego wartości w punktach
zdefiniowany poprzez jego wartości w punktach 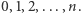 Naszym zadaniem jest wyznaczenie wartości tego wielomianu w punkcie
Naszym zadaniem jest wyznaczenie wartości tego wielomianu w punkcie 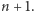
Oznaczmy współczynniki wielomianu 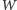 przez ciąg liczb
przez ciąg liczb 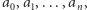 gdzie
gdzie 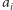 oznacza współczynnik przy
oznacza współczynnik przy 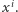 Najprostszym sposobem rozwiązania tego zadania jest wyznaczenie współczynników wielomianu
Najprostszym sposobem rozwiązania tego zadania jest wyznaczenie współczynników wielomianu 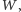 rozwiązując następujący układ równań liniowych:
rozwiązując następujący układ równań liniowych:

Można to zrealizować za pomocą metody eliminacji Gaussa. Niestety, ten algorytm jest zbyt powolny, ponieważ wykonuje on 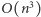 operacji na liczbach, które mogą rosnąć wykładniczo. Metodę tę można jednak znacznie przyśpieszyć, wykorzystując fakt, że znamy wartości wielomianu
operacji na liczbach, które mogą rosnąć wykładniczo. Metodę tę można jednak znacznie przyśpieszyć, wykorzystując fakt, że znamy wartości wielomianu 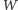 w punktach będących kolejnymi liczbami naturalnymi.
w punktach będących kolejnymi liczbami naturalnymi.
Dowód. Skoro funkcje 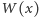 oraz
oraz 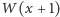 są wielomianami, to również funkcja
są wielomianami, to również funkcja 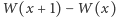 jest wielomianem. Współczynnik wielomianu
jest wielomianem. Współczynnik wielomianu 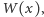 przy
przy 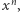 wynosi
wynosi 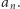 Natomiast dla wielomianu
Natomiast dla wielomianu 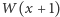 mamy:
mamy:

Skoro 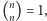 to współczynnik przy
to współczynnik przy 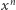 wielomianu
wielomianu 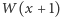 także jest równy
także jest równy 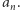 Z tego wynika, że współczynnik przy
Z tego wynika, że współczynnik przy 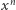 wielomianu
wielomianu 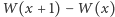 jest równy
jest równy 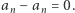
Korzystając z lematu 1, możemy zredukować stopień wielomianu 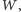 uzyskując problem równoważny. Aby to zrobić, zdefiniujmy ciąg wielomianów
uzyskując problem równoważny. Aby to zrobić, zdefiniujmy ciąg wielomianów 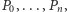 taki że
taki że 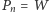 oraz
oraz 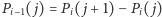 dla
dla 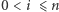 oraz
oraz 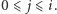 Powstały w ten sposób wielomian
Powstały w ten sposób wielomian 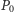 ma stopień
ma stopień 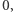 zatem
zatem 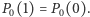 Znając wartość wielomianu
Znając wartość wielomianu 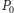 w kolejnym punkcie, możemy obliczyć wartości
w kolejnym punkcie, możemy obliczyć wartości 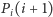 dla
dla 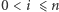 bezpośrednio z definicji ciągu wielomianów
bezpośrednio z definicji ciągu wielomianów 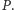 Obliczając nowe wartości kolejnych wielomianów, za każdym razem do poprzednio otrzymanej wartości dodajemy
Obliczając nowe wartości kolejnych wielomianów, za każdym razem do poprzednio otrzymanej wartości dodajemy 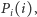 zatem:
zatem:

Spróbujmy teraz zapisać 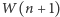 w zależności od wartości
w zależności od wartości 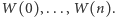 Skoro jedynymi operacjami, jakie wykonujemy, są dodawanie i odejmowanie, to wszystkie otrzymane liczby będą liniowo zależne od wartości wielomianu
Skoro jedynymi operacjami, jakie wykonujemy, są dodawanie i odejmowanie, to wszystkie otrzymane liczby będą liniowo zależne od wartości wielomianu 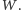 Możemy, korzystając z definicji ciągu wielomianów
Możemy, korzystając z definicji ciągu wielomianów 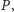 zapisać:
zapisać:
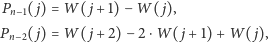 |
oraz w ogólności:

Zachęcam Czytelnika, aby sprawdził poprawność tego wzoru i spróbował go udowodnić za pomocą indukcji matematycznej. Po wstawieniu tej równości do wzoru otrzymanego w poprzednim akapicie dostajemy:
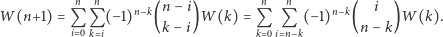 |
Dowód. Udowodnimy ją za pomocą indukcji względem 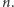 Dla
Dla 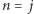 mamy
mamy

W kroku indukcyjnym korzystamy z tożsamości:
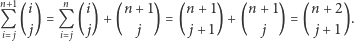 |
Na podstawie lematu 2 otrzymujemy dla 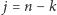 :
:
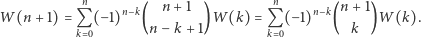 |
Dzięki tożsamości

możemy obliczyć powyższą sumę, wykonując liniową ilość operacji na liczbach całkowitych.
Wartości składników tej sumy mogą być bardzo duże, więc dodatkową trudność w tym zadaniu są operacje na dużych liczbach. Na szczęście potrzebujemy jedynie wykonywać sumowanie dużych liczb oraz mnożenie i dzielenie dużych liczb przez małe. Obie te operacje można łatwo zrealizować w czasie liniowym względem długości liczby. Zatem ostatecznie otrzymujemy złożoność czasową