Zapis wieżowy
Tym razem omówimy rozwiązanie zadania Zapis wieżowy z Akademickich Mistrzostw Polski w Programowaniu Zespołowym z 2006 roku.
Dla ciągu  liczb naturalnych
liczb naturalnych 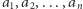 oraz liczby naturalnej
oraz liczby naturalnej 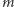 należy wyznaczyć resztę z dzielenia przez
należy wyznaczyć resztę z dzielenia przez 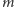 wieży potęgowej, w której liczby z ciągu są kolejnymi wykładnikami. Innymi słowy, mamy znaleźć wartość wyrażenia
wieży potęgowej, w której liczby z ciągu są kolejnymi wykładnikami. Innymi słowy, mamy znaleźć wartość wyrażenia
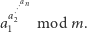 |
Przykładowo, 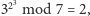 gdyż
gdyż 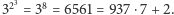 Oczywiście, bezpośrednie obliczanie potęg nie wchodzi w grę, gdyż ich wartości rosną coraz szybciej z każdym dodatkowym wykładnikiem i już liczba
Oczywiście, bezpośrednie obliczanie potęg nie wchodzi w grę, gdyż ich wartości rosną coraz szybciej z każdym dodatkowym wykładnikiem i już liczba 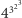 ma 3951 cyfr. Dla uproszczenia zapisu wieżę potęgową będziemy oznaczali przez
ma 3951 cyfr. Dla uproszczenia zapisu wieżę potęgową będziemy oznaczali przez 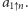
W rozwiązaniu zadania pomoże nam twierdzenie Eulera, które mówi, że dla względnie pierwszych liczb naturalnych 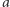 i
i 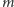 spełniona jest kongruencja
spełniona jest kongruencja
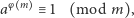 |
(*) |
gdzie 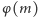 oznacza liczbę liczb względnie pierwszych z
oznacza liczbę liczb względnie pierwszych z 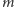 i nie większych niż ta liczba. Jeśli zatem liczby
i nie większych niż ta liczba. Jeśli zatem liczby 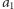 i
i 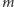 byłyby względnie pierwsze, to moglibyśmy:
byłyby względnie pierwsze, to moglibyśmy:
- wyznaczyć
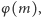
- rekurencyjnie obliczyć rozwiązanie mniejszego problemu dla ciągu
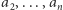 i modułu
i modułu 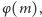 czyli
czyli 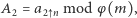
- korzystając z twierdzenia Eulera, wyznaczyć rozwiązanie
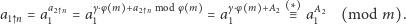 |
Przypomnijmy, że jeśli znamy rozkład modułu na czynniki pierwsze 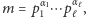 to do obliczenia
to do obliczenia 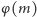 możemy wykorzystać następujący wzór:
możemy wykorzystać następujący wzór:
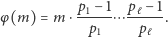 |
(**) |
Rozkład ten możemy znaleźć w czasie 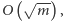 przeglądając wszystkie potencjalne dzielniki liczby
przeglądając wszystkie potencjalne dzielniki liczby  nie większe niż
nie większe niż 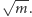 Zatem w takim też czasie wykonamy krok 1 algorytmu. Z kolei potęgowanie
Zatem w takim też czasie wykonamy krok 1 algorytmu. Z kolei potęgowanie 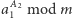 z kroku 3 możemy wykonać w czasie
z kroku 3 możemy wykonać w czasie 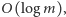 stosując metodę wielokrotnego podnoszenia do kwadratu. W sumie wykonamy
stosując metodę wielokrotnego podnoszenia do kwadratu. W sumie wykonamy 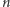 wywołań rekurencyjnych, w
wywołań rekurencyjnych, w 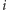 -tym wywołaniu obliczając
-tym wywołaniu obliczając 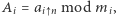 gdzie
gdzie 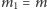 oraz
oraz 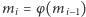 dla
dla 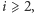 co da algorytm o złożoności czasowej
co da algorytm o złożoności czasowej 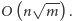
Zauważmy jednak, że ze wzoru 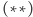 widać, iż
widać, iż 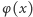 dla nieparzystego
dla nieparzystego  jest liczbą parzystą, natomiast dla parzystego
jest liczbą parzystą, natomiast dla parzystego 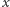 mamy
mamy 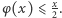 Wynika z tego, że ciąg kolejnych modułów
Wynika z tego, że ciąg kolejnych modułów 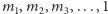 ma co najwyżej
ma co najwyżej 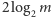 wyrazów, zatem wystarczy, że wykonamy
wyrazów, zatem wystarczy, że wykonamy 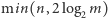 wywołań rekurencyjnych. A po drugie, pracę wykonaną we wszystkich wywołaniach kroku 1 można sumarycznie oszacować przez
wywołań rekurencyjnych. A po drugie, pracę wykonaną we wszystkich wywołaniach kroku 1 można sumarycznie oszacować przez 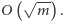 Zatem lepszym oszacowaniem czasu działania naszego algorytmu jest
Zatem lepszym oszacowaniem czasu działania naszego algorytmu jest 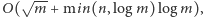 czyli po prostu
czyli po prostu 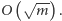
Niestety, abyśmy mieli pewność, że algorytm działa poprawnie, nie tylko liczby 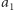 i
i  muszą być względnie pierwsze, ale również liczby
muszą być względnie pierwsze, ale również liczby 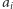 i
i 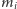 dla wszystkich
dla wszystkich 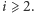 Na szczęście twierdzenie Eulera można uogólnić, aby działało również bez założenia o względnej pierwszości. Nowa wersja brzmi następująco: dla dowolnych liczb naturalnych
Na szczęście twierdzenie Eulera można uogólnić, aby działało również bez założenia o względnej pierwszości. Nowa wersja brzmi następująco: dla dowolnych liczb naturalnych 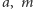 i
i 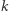 spełniona jest kongruencja
spełniona jest kongruencja
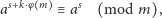 |
(***) |
gdzie  jest pewną liczbą zależną od
jest pewną liczbą zależną od 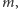 jednak nie większą niż
jednak nie większą niż 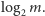
Zanim udowodnimy to twierdzenie, zobaczmy, jak dzięki niemu naprawić nasz algorytm. Zmodyfikujemy go tak, aby nie tylko obliczał wartości 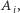 ale również dodatkowy bit
ale również dodatkowy bit 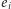 równy 1 wtedy, gdy
równy 1 wtedy, gdy 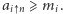 Znowu pokażemy, jak wykonać krok (2) algorytmu: załóżmy zatem, że
Znowu pokażemy, jak wykonać krok (2) algorytmu: załóżmy zatem, że 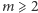 i obliczyliśmy już
i obliczyliśmy już 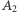 oraz
oraz 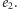
Wyznaczmy 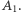 Jeśli
Jeśli 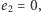 to
to 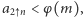 więc
więc 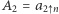 i wystarczy przyjąć
i wystarczy przyjąć 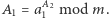 Z kolei jeśli
Z kolei jeśli 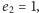 to
to 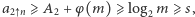 czyli
czyli
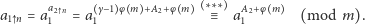 |
Zatem w obu przypadkach mamy 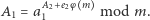 Z kolei wyznaczyć
Z kolei wyznaczyć 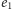 można następująco: jeśli
można następująco: jeśli 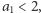 to
to 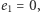 a w przeciwnym przypadku możemy wykonać potęgowanie
a w przeciwnym przypadku możemy wykonać potęgowanie 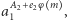 w każdej iteracji domnażając jedno
w każdej iteracji domnażając jedno 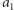 i sprawdzając, czy wynik osiągnął już
i sprawdzając, czy wynik osiągnął już  (wykonamy co najwyżej
(wykonamy co najwyżej 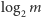 takich iteracji). Ostatecznie złożoność czasowa całego algorytmu nie zmienia się.
takich iteracji). Ostatecznie złożoność czasowa całego algorytmu nie zmienia się.
Pozostaje udowodnić dane wzorem 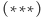 uogólnienie twierdzenia Eulera. Zdefiniujmy ciąg
uogólnienie twierdzenia Eulera. Zdefiniujmy ciąg 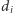 następująco:
następująco:
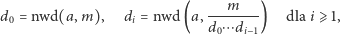 |
oraz niech  będzie najmniejszą liczbą, taką że
będzie najmniejszą liczbą, taką że 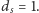 Oznaczmy też
Oznaczmy też 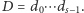
Liczba 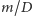 jest liczbą powstałą po usunięciu z
jest liczbą powstałą po usunięciu z 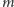 wszystkich czynników pierwszych występujących w
wszystkich czynników pierwszych występujących w 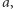 zatem liczby
zatem liczby 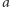 i
i 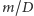 są względnie pierwsze. Z twierdzenia Eulera wynika zatem, że
są względnie pierwsze. Z twierdzenia Eulera wynika zatem, że
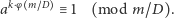 |
Ponadto każda z liczb 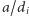 jest całkowita, więc liczba
jest całkowita, więc liczba 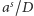 również. Mnożąc powyższe równanie przez
również. Mnożąc powyższe równanie przez 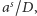 dostajemy
dostajemy
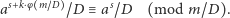 |
Korzystając z faktu, że kongruencja 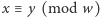 jest spełniona wtedy i tylko wtedy, gdy spełniona jest
jest spełniona wtedy i tylko wtedy, gdy spełniona jest 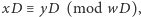 możemy przemnożyć przez
możemy przemnożyć przez 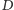 obie strony i moduł powyższego równania:
obie strony i moduł powyższego równania:
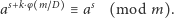 |
Liczby 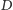 i
i 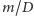 są względnie pierwsze, zatem z multiplikatywności funkcji
są względnie pierwsze, zatem z multiplikatywności funkcji 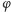 dostajemy
dostajemy 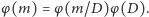 Ponadto wykładniki w rozkładach na czynniki pierwsze liczb
Ponadto wykładniki w rozkładach na czynniki pierwsze liczb 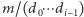 zmniejszają się, więc
zmniejszają się, więc 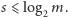 Zatem ostatecznie dostajemy tezę twierdzenia:
Zatem ostatecznie dostajemy tezę twierdzenia:
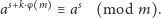 |