Drobiazgi
Odwracamy, obracamy...
Dana jest 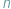 -elementowa tablica
-elementowa tablica ![a[1::n];](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/2x-8d66b826766d0f12e412cfa451e4c3abe561de48-im-65,9A,A1-FF,FF,FF.gif) którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności
którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności ![|a[n];a[n −1]; :::;a[1]:](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/3x-8d66b826766d0f12e412cfa451e4c3abe561de48-im-65,9A,A1-FF,FF,FF.gif)
Najłatwiej to zrobić w miejscu (czyli używając jedynie stałej liczby komórek pamięci dla zmiennych pomocniczych), korzystając z instrukcji ![|swap(a[i], a[ j])](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/1x-eeca35f3c96f78919d0c4aa76297bb54621f036a-im-33,33,33-FF,FF,FF.gif) zamieniającej miejscami wartości dwóch elementów:
zamieniającej miejscami wartości dwóch elementów:
![for i = 1 to⌊n/2⌋ do swap(a[i],a[n + 1− i]);](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/2x-eeca35f3c96f78919d0c4aa76297bb54621f036a-dm-33,33,33-FF,FF,FF.gif)
Nietrudno się przekonać, że powyższy kod wywołuje instrukcję zamiany jedynie 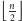 razy, co w przypadku odwrócenia tablicy jest wynikiem optymalnym.
razy, co w przypadku odwrócenia tablicy jest wynikiem optymalnym.
A teraz trudniejsze zadanie: chcemy tę samą tablicę obrócić o 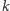 komórek w lewo, czyli ustawić jej elementy w kolejności
komórek w lewo, czyli ustawić jej elementy w kolejności ![|a[k+ 1],a[k +2],...,a[n],a[1],...,a[k].](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/2x-19ed7f213ccc78fff4d5be9c684c292c76c70b6f-im-33,33,33-FF,FF,FF.gif) I tym razem spróbujmy to zrobić, używając jedynie instrukcji zamiany.
I tym razem spróbujmy to zrobić, używając jedynie instrukcji zamiany.
Można w tym celu trzykrotnie wywołać omówioną przed chwilą procedurę odwracania tablicy:
![rev(a[1..k]);rev(a[k+ 1..n]);rev(a[1..n]);](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/1x-4825c3ff5c125eafa506f38f0866aee080d6502a-dm-33,33,33-FF,FF,FF.gif)
Ten kod wykona 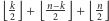 instrukcji zamiany, co w zależności od parzystości liczb
instrukcji zamiany, co w zależności od parzystości liczb 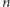 i
i 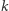 da nam
da nam  lub
lub 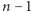 instrukcji. Pytanie: czy da się mniej?
instrukcji. Pytanie: czy da się mniej?
Poniższy kod obraca tablicę, dzieląc ją na 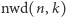 cykli o długości
cykli o długości 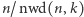 i wykonując obrót każdego z nich niezależnie, do czego potrzebuje
i wykonując obrót każdego z nich niezależnie, do czego potrzebuje 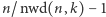 instrukcji zamiany:
instrukcji zamiany:
![for i = 1 to nwd(n, k) do for j = 1 to n/ nwd(n, k)− 1 do swap(a[i +n ( j −1) ⋅k],a[i +n j⋅k]);](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/4x-1f59b0acf527d3ca888e45eaa03768f686d61d24-dm-33,33,33-FF,FF,FF.gif)
Operacja 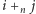 oznacza tu
oznacza tu 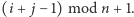 Zatem w tym rozwiązaniu użyjemy w sumie
Zatem w tym rozwiązaniu użyjemy w sumie 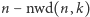 instrukcji zamiany. A czy ten wynik da się poprawić?
instrukcji zamiany. A czy ten wynik da się poprawić?