Algorytmy (I)
W rozważaniach naszych nie będziemy chwilowo dążyli do ścisłej definicji algorytmu ani do formalizacji zapisu algorytmów. Celem naszym będzie wyrobienie u Czytelnika przekonania, że algorytm jest uściśleniem przepisu postępowania prowadzącego do zamierzonego celu.
Spróbujemy wymienić kilka charakterystycznych cech (nieformalnego) pojęcia algorytmu.
- Algorytm określa się przez podanie przepisu postępowania, pamięci oraz sterowania.
- Pamięć określa się jako zbiór, którego elementy nazywamy stanami.
- Sterowanie (którego role może pełnić człowiek lub urządzenie) umożliwia przeprowadzenie obliczeń, a mianowicie w oparciu o przepis postępowania wyznacza jednoznacznie czynność, którą należy wykonać na aktualnym stanie pamięci oraz określa jednoznacznie następny stan pamięci i następną czynność do wykonania (jeśli jeszcze jakąś czynność należy wykonać).
- Dla każdego algorytmu określony jest sposób wprowadzania do pamięci elementów zbioru nazywanego zbiorem danych oraz sposób odczytywania wyników z pamięci.
Aby wyjaśnić bliżej sens powyższych sformułowań rozważmy dobrze znany algorytm Euklidesa, który pozwala dla dowolnych liczb naturalnych 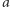 i
i 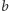 wyznaczyć ich największy wspólny dzielnik oznaczany przez
wyznaczyć ich największy wspólny dzielnik oznaczany przez 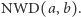 Jeśli chcemy wyznaczyć
Jeśli chcemy wyznaczyć 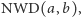 gdzie
gdzie 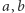 są liczbami naturalnymi, postępujemy według następujących reguł:
są liczbami naturalnymi, postępujemy według następujących reguł:
- (1)
- Jeśli
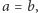 to
to 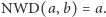
- (2)
- Chcąc znaleźć
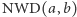 gdy
gdy 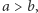 dzielimy
dzielimy 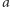 przez
przez 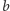 i wyznaczamy resztę
i wyznaczamy resztę  z tego dzielenia. Z kolei dzielimy
z tego dzielenia. Z kolei dzielimy 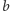 przez
przez  i wyznaczamy nową resztę
i wyznaczamy nową resztę 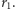 Następnie dzielimy
Następnie dzielimy  przez
przez 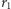 i wyznaczamy nową resztę
i wyznaczamy nową resztę 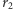 itd., aż dojdziemy do reszty 0. Ostatnia różna od zera reszta będzie największym wspólnym dzielnikiem liczb
itd., aż dojdziemy do reszty 0. Ostatnia różna od zera reszta będzie największym wspólnym dzielnikiem liczb  i
i 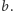
- (3)
- Jeśli
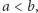 to postępujemy jak w (2) zamieniając rolami
to postępujemy jak w (2) zamieniając rolami 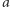 i
i 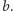 Przyjmiemy, że liczby naturalne będą przedstawiane w zapisie dziesiętnym i jeśli nie zajdzie potrzeba, nie będziemy odróżniać liczby naturalnej od jej zapisu dziesiętnego.
Przyjmiemy, że liczby naturalne będą przedstawiane w zapisie dziesiętnym i jeśli nie zajdzie potrzeba, nie będziemy odróżniać liczby naturalnej od jej zapisu dziesiętnego.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (389 KB)