Informatyczny kącik olimpijski
Zliczamy puste prostokąty
W tym miesiącu zajmiemy się dość klasycznym zadaniem. Dany jest kwadrat rozmiaru 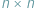 podzielony na
podzielony na 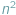 pól, przy czym niektóre pola są zabronione. Dowolny zawarty w tym kwadracie prostokąt, który nie zawiera żadnego pola zabronionego, nazwiemy prostokątem pustym. Należy znaleźć pusty prostokąt o jak największym polu.
pól, przy czym niektóre pola są zabronione. Dowolny zawarty w tym kwadracie prostokąt, który nie zawiera żadnego pola zabronionego, nazwiemy prostokątem pustym. Należy znaleźć pusty prostokąt o jak największym polu.

Rys. 1 Przykładowy kwadrat rozmiaru 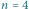 z czterema polami zabronionymi (zaznaczone krzyżykami). Największy pusty prostokąt ma rozmiar
z czterema polami zabronionymi (zaznaczone krzyżykami). Największy pusty prostokąt ma rozmiar 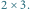 Poniższa tabelka przedstawia liczności pustych prostokątów dla wszystkich rozmiarów
Poniższa tabelka przedstawia liczności pustych prostokątów dla wszystkich rozmiarów 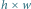 :
:

To zadanie nie powinno być nowością ani dla miłośników zadań olimpijskich (pojawiło się m.in. na IX Olimpiadzie Informatycznej jako zadanie pt. Działka), ani dla stałych czytelników Delty (omawialiśmy jego rozwiązanie w artykule Prostokąt arytmetyczny w numerze 3/2012). Co więcej, różne modyfikacje tego zadania pojawiały się też (i nadal pojawiają) na innych konkursach. Przykładowe modyfikacje mogą polegać na tym, że jesteśmy proszeni o znalezienie pustego prostokąta o największym obwodzie, liczby pustych prostokątów czy też sumarycznego pola powierzchni wszystkich pustych prostokątów. I choć główna idea rozwiązania wszystkich tych wersji zadania jest taka sama, to różnią się one w szczegółach, które każdorazowo trzeba dopracować. Tutaj przedstawimy dość ogólną metodę, która pozwoli nam bardzo łatwo rozwiązywać podobne zadania. A mianowicie pokażemy, jak wyznaczyć w sumarycznym czasie 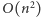 liczbę pustych prostokątów rozmiaru
liczbę pustych prostokątów rozmiaru 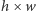 dla wszystkich wartości
dla wszystkich wartości 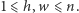
Pole leżące na przecięciu 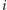 -tego wiersza i
-tego wiersza i 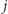 -tej kolumny kwadratu będzie miało współrzędne
-tej kolumny kwadratu będzie miało współrzędne 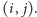 Przede wszystkim dla każdego pola
Przede wszystkim dla każdego pola 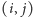 będziemy chcieli znać liczbę niezabronionych pól leżących powyżej niego (włącznie z tym polem); oznaczymy tę wartość przez
będziemy chcieli znać liczbę niezabronionych pól leżących powyżej niego (włącznie z tym polem); oznaczymy tę wartość przez ![|d[i, j].](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/5x-603df3023a27fc2bf2064a4366ac1e8c26b3ae37-im-33,33,33-FF,FF,FF.gif) Całą tablicę
Całą tablicę 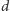 łatwo obliczyć w czasie
łatwo obliczyć w czasie 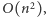 gdyż
gdyż ![d[i, j] = 0,](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/8x-603df3023a27fc2bf2064a4366ac1e8c26b3ae37-im-33,33,33-FF,FF,FF.gif) jeśli pole
jeśli pole 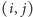 jest zabronione oraz
jest zabronione oraz ![d[i, j] = d[i− 1, j] +1](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/10x-603df3023a27fc2bf2064a4366ac1e8c26b3ae37-im-33,33,33-FF,FF,FF.gif) w przeciwnym przypadku. Dla uproszczenia zakładamy również, że wszystkie pola poza kwadratem są zabronione i
w przeciwnym przypadku. Dla uproszczenia zakładamy również, że wszystkie pola poza kwadratem są zabronione i ![d[i,0] = d[i,n + 1] = 0.](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/11x-603df3023a27fc2bf2064a4366ac1e8c26b3ae37-im-33,33,33-FF,FF,FF.gif)
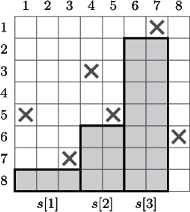
Rys. 2 Zacieniono trzy prostokąty, które reprezentują obszar dla pola 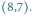 Poniższa tabelka przedstawia zawartość stosu dla pól
Poniższa tabelka przedstawia zawartość stosu dla pól 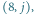 gdy
gdy 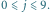

Rozwiązanie podzielimy na  faz; w
faz; w 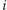 -tej fazie będziemy rozpatrywać prostokąty, których dolny bok zawiera pola z
-tej fazie będziemy rozpatrywać prostokąty, których dolny bok zawiera pola z 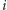 -tego wiersza. Ustalmy pewne pole
-tego wiersza. Ustalmy pewne pole 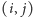 i rozważmy wszystkie puste prostokąty, których prawy dolny róg znajduje się na tym polu. Zbiór wszystkich pól, w których może znajdować się lewy górny róg takiego pustego prostokąta, jest obszarem, którego górny obrys składa się z odcinków idących w prawo i do góry. Taki obszar będziemy reprezentowali jako sumę minimalnej liczby rozłącznych prostokątów o coraz większych wysokościach, których dolne boki dotykają
i rozważmy wszystkie puste prostokąty, których prawy dolny róg znajduje się na tym polu. Zbiór wszystkich pól, w których może znajdować się lewy górny róg takiego pustego prostokąta, jest obszarem, którego górny obrys składa się z odcinków idących w prawo i do góry. Taki obszar będziemy reprezentowali jako sumę minimalnej liczby rozłącznych prostokątów o coraz większych wysokościach, których dolne boki dotykają 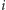 -tego wiersza (Rys. 2). Rozmiary
-tego wiersza (Rys. 2). Rozmiary 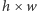 kolejnych prostokątów będziemy trzymać na stosie, co umożliwi nam łatwe uaktualnianie tej reprezentacji, jeśli będziemy przeglądać kolumny od lewej do prawej.
kolejnych prostokątów będziemy trzymać na stosie, co umożliwi nam łatwe uaktualnianie tej reprezentacji, jeśli będziemy przeglądać kolumny od lewej do prawej.
Stos będziemy trzymać w tablicy  (wysokości i szerokości
(wysokości i szerokości 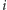 -tego prostokąta na stosie to odpowiednio
-tego prostokąta na stosie to odpowiednio ![s[i].h](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/3x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![s[i].w](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/4x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-im-33,33,33-FF,FF,FF.gif) ), a liczbę jego elementów w zmiennej
), a liczbę jego elementów w zmiennej 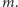 Poniższy pseudokod pokazuje, jak uaktualnić zawartość stosu dla pola
Poniższy pseudokod pokazuje, jak uaktualnić zawartość stosu dla pola 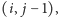 aby odpowiadała ona polu
aby odpowiadała ona polu 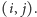 Dopóki wysokość
Dopóki wysokość ![s[m].h](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/8x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-im-33,33,33-FF,FF,FF.gif) najwyższego prostokąta na stosie jest co najmniej tak duża jak
najwyższego prostokąta na stosie jest co najmniej tak duża jak ![|d[i, j],](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/9x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-im-33,33,33-FF,FF,FF.gif) to usuwamy go ze stosu. Następnie wrzucamy na stos prostokąt rozmiaru
to usuwamy go ze stosu. Następnie wrzucamy na stos prostokąt rozmiaru ![d[i, j]× w,](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/10x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 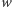 jest sumaryczną długością wszystkich usuniętych prostokątów plus 1.
jest sumaryczną długością wszystkich usuniętych prostokątów plus 1.
![w whilem inc(w, dec(m); inc(m); s[m].w s[m].h](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/12x-9bc67cf05a00dbea6d7589f891f3eec6c198db81-dm-33,33,33-FF,FF,FF.gif)
Zauważmy, że każdy prostokąt usuwany ze stosu jest kandydatem na największy pusty prostokąt. Co więcej, wystarczy, że rozpatrzymy tylko tych kandydatów. Ponieważ dla ustalonego 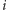 liczba operacji wykonanych na stosie jest
liczba operacji wykonanych na stosie jest 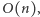 gdyż wrzucamy na niego
gdyż wrzucamy na niego  elementów, zatem cały algorytm działa w czasie
elementów, zatem cały algorytm działa w czasie 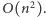
Aby wyznaczyć liczbę pustych prostokątów wszystkich rozmiarów, postąpimy nieco sprytniej. Zachowamy następujący niezmiennik: jeśli znajdujemy się na polu 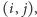 to znaczy, że policzyliśmy już te puste prostokąty, których prawy dolny róg jest na polu
to znaczy, że policzyliśmy już te puste prostokąty, których prawy dolny róg jest na polu 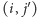 dla
dla 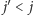 i jednocześnie nie są one zawarte w obszarze dla pola
i jednocześnie nie są one zawarte w obszarze dla pola 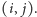
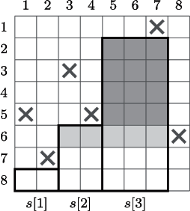
Rys. 3 Rozważając pole 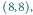 usuwamy element
usuwamy element 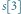 ze stosu. Musimy wtedy policzyć
ze stosu. Musimy wtedy policzyć 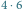 prostokątów mających prawy dolny róg na polu
prostokątów mających prawy dolny róg na polu 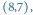 a lewy górny w ciemno zacienionym obszarze. Jest tam
a lewy górny w ciemno zacienionym obszarze. Jest tam 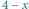 prostokątów rozmiaru
prostokątów rozmiaru 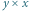 dla
dla 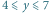 i
i 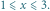
Następnie usuwamy element 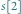 ze stosu, co powoduje zliczenie 15 prostokątów z jasno zacienionego obszaru (
ze stosu, co powoduje zliczenie 15 prostokątów z jasno zacienionego obszaru ( 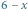 prostokątów rozmiaru
prostokątów rozmiaru 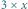 dla
dla 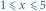 ).
).
Zatem zwiększanie obszaru (poprzez wrzucanie nowych elementów na stos) nigdy nie będzie zmieniać liczności rozważonych pustych prostokątów, natomiast usuwanie elementów ze stosu może powodować konieczność aktualizacji. Wszystkie pola usuniętego prostokąta ![s[m],](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/1x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) które znajdują się w odległości co najmniej
które znajdują się w odległości co najmniej 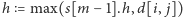 od wiersza
od wiersza 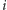 na pewno zostaną usunięte z obszaru (zakładamy przy tym, że
na pewno zostaną usunięte z obszaru (zakładamy przy tym, że ![s[0].h = 0](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/4x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) ). Musimy zatem policzyć puste prostokąty zawarte w prostokącie
). Musimy zatem policzyć puste prostokąty zawarte w prostokącie ![s[m],](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/5x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) które przestaną być w tym obszarze zawarte, czyli ich lewy górny róg jest jednym z pól, które zostaną usunięte z obszaru. Te prostokąty mają wysokości od
które przestaną być w tym obszarze zawarte, czyli ich lewy górny róg jest jednym z pól, które zostaną usunięte z obszaru. Te prostokąty mają wysokości od 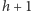 do
do ![|s[m].h](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/7x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) oraz szerokości od 1 do
oraz szerokości od 1 do ![s[m].w, |](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/8x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) przy czym prostokątów o rozmiarze
przy czym prostokątów o rozmiarze 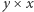 jest
jest ![s[m].w](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/10x-43283f13723f8dec70eae3fe8c096be54cf3b9ec-im-33,33,33-FF,FF,FF.gif) (Rys. 3).
(Rys. 3).
Należy też uważnie rozważyć przypadek, gdy dla danego pola 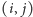 usuwamy więcej niż jeden element ze stosu. Wtedy szerokość aktualnie usuwanego elementu należy zwiększyć o szerokości usuniętych poprzednio (wygodnie jest tu korzystać z wprowadzonej już zmiennej
usuwamy więcej niż jeden element ze stosu. Wtedy szerokość aktualnie usuwanego elementu należy zwiększyć o szerokości usuniętych poprzednio (wygodnie jest tu korzystać z wprowadzonej już zmiennej 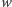 ).
).
Jeśli zatem liczności pustych prostokątów będziemy zapisywać w tablicy  (gdzie
(gdzie ![| c[y,x]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/2x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) oznacza liczbę pustych prostokątów rozmiaru
oznacza liczbę pustych prostokątów rozmiaru 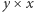 ), to mamy do rozwiązania następujący problem: dla danych liczb
), to mamy do rozwiązania następujący problem: dla danych liczb 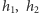 i
i 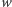 chcemy szybko wykonywać operację zwiększania komórek
chcemy szybko wykonywać operację zwiększania komórek ![c[y,x]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/6x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) o wartość
o wartość 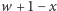 dla
dla 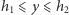 oraz
oraz 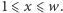 Nie możemy, oczywiście, pozwolić sobie na zrobienie tego zupełnie naiwnie. Zakładając, że początkowo w tablicy
Nie możemy, oczywiście, pozwolić sobie na zrobienie tego zupełnie naiwnie. Zakładając, że początkowo w tablicy  są same zera, zastosujemy następujący trik: do komórki
są same zera, zastosujemy następujący trik: do komórki ![|c[h1,w]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/11x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) wpiszemy 1, a do komórki
wpiszemy 1, a do komórki ![c[h2 | + 1,w]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/12x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) wpiszemy
wpiszemy 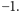 Następnie niezależnie w każdej kolumnie tablicy
Następnie niezależnie w każdej kolumnie tablicy  obliczymy sumy prefiksowe. To spowoduje, że jedynki znajdą się w komórkach
obliczymy sumy prefiksowe. To spowoduje, że jedynki znajdą się w komórkach ![| c[y,w]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/15x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) dla
dla 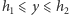 (a
(a 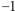 zniknie). Następnie w każdym wierszu obliczymy "trochę lepsze" sumy sufiksowe, które każdą jedynkę w komórce
zniknie). Następnie w każdym wierszu obliczymy "trochę lepsze" sumy sufiksowe, które każdą jedynkę w komórce ![|c[y,x]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/18x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) zamienią na ciąg liczb
zamienią na ciąg liczb 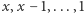 w komórkach
w komórkach ![|c[y,1],c[y,2],...,c[y,x].](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/20x-2e75e3ccf7dc88ef3dd9b501fd1957f4b0720da4-im-33,33,33-FF,FF,FF.gif) Po takich manipulacjach tablica
Po takich manipulacjach tablica  ma wartości zgodne z pojedynczą operacją zwiększania.
ma wartości zgodne z pojedynczą operacją zwiększania.
Nietrudno się przekonać, że jeśli chcemy wykonać więcej niż jedną operację zwiększania, to możemy najpierw zwiększyć wszystkie komórki ![c[h1,w]](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/1x-90be69183a4b97137ab195de95ec036e716107b8-im-33,33,33-FF,FF,FF.gif) o jeden i zmniejszyć odpowiadające im komórki
o jeden i zmniejszyć odpowiadające im komórki ![|c[h + 1,w] 2](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/2x-90be69183a4b97137ab195de95ec036e716107b8-im-33,33,33-FF,FF,FF.gif) o jeden, a dopiero na sam koniec jeden raz obliczyć powyższe sumy. Łącznie zajmie to czas
o jeden, a dopiero na sam koniec jeden raz obliczyć powyższe sumy. Łącznie zajmie to czas 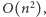 a pseudokod algorytmu może wyglądać następująco:
a pseudokod algorytmu może wyglądać następująco:

![for i = 1ton do for j = 0to n +1 do w while m h = max(s[m inc(w, inc(c[h + 1,w]); dec(c[s[m].h dec(m); inc(m); s[m].w s[m].h for i = 1ton do for j = 1to n do inc(c[i + 1, j],c[i, j]); c1 = c2 = 0; for j = n downto 1 do inc(c1,c[i, j]); inc(c ,c ); 2 1 c[i, j] = c2;](/math/temat/informatyka/algorytmy/2015/10/27/Zliczamy_puste_prostokaty/1x-311a1bbcc38522e2ca7030ac85cad15a2dea8c31-dm-33,33,33-FF,FF,FF.gif)
Jako ćwiczenie dla Czytelnika proponujemy modyfikację tego algorytmu, aby dla każdego rozmiaru wyznaczał liczbę maksymalnych pustych prostokątów, czyli takich, które nie są zawarte w żadnym większym pustym prostokącie.
 z czterema polami zabronionymi (zaznaczone krzyżykami). Największy pusty prostokąt ma rozmiar
z czterema polami zabronionymi (zaznaczone krzyżykami). Największy pusty prostokąt ma rozmiar 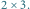 Poniższa tabelka przedstawia liczności pustych prostokątów dla wszystkich rozmiarów
Poniższa tabelka przedstawia liczności pustych prostokątów dla wszystkich rozmiarów 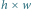 :
: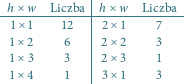
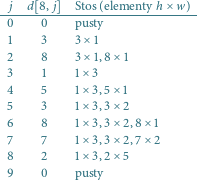
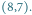 Poniższa tabelka przedstawia zawartość stosu dla pól
Poniższa tabelka przedstawia zawartość stosu dla pól 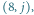 gdy
gdy 
 usuwamy element
usuwamy element 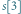 ze stosu. Musimy wtedy policzyć
ze stosu. Musimy wtedy policzyć 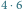 prostokątów mających prawy dolny róg na polu
prostokątów mających prawy dolny róg na polu 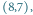 a lewy górny w ciemno zacienionym obszarze. Jest tam
a lewy górny w ciemno zacienionym obszarze. Jest tam 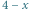 prostokątów rozmiaru
prostokątów rozmiaru 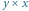 dla
dla 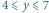 i
i 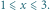
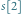 ze stosu, co powoduje zliczenie 15 prostokątów z jasno zacienionego obszaru (
ze stosu, co powoduje zliczenie 15 prostokątów z jasno zacienionego obszaru ( 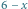 prostokątów rozmiaru
prostokątów rozmiaru 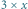 dla
dla 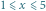 ).
).