Zliczamy skojarzenia (I). O układaniu domina i permanencie
Zajmiemy się takim oto zadaniem: dana jest szachownica rozmiaru 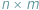 i
i  kostek domina, z których każda może przykryć dwa sąsiednie pola szachownicy. Na ile sposobów możemy przykryć całą szachownicę?
kostek domina, z których każda może przykryć dwa sąsiednie pola szachownicy. Na ile sposobów możemy przykryć całą szachownicę?

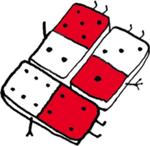
Rys. 1 Dwa spośród 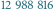 przykryć szachownicy rozmiaru
przykryć szachownicy rozmiaru 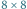 za pomocą 32 kostek domina.
za pomocą 32 kostek domina.
Przyjmujemy, że dwa sposoby są różne, jeśli istnieją dwa pola przykryte w pierwszym sposobie tą samą kostką, a w drugim sposobie różnymi kostkami (Rys. 1).
Przykładowo, szachownicę rozmiaru 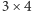 można przykryć sześcioma kostkami na 11 sposobów (uzyskujemy
można przykryć sześcioma kostkami na 11 sposobów (uzyskujemy 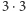 sposobów, jeśli przykrywamy niezależnie lewą i prawą połówkę, oraz dodatkowe 2 sposoby, gdy istnieją kostki leżące na obu połówkach):
sposobów, jeśli przykrywamy niezależnie lewą i prawą połówkę, oraz dodatkowe 2 sposoby, gdy istnieją kostki leżące na obu połówkach):

Aby rozwiązać to zadanie, naszą szachownicę przedstawimy jako graf. Każdemu polu szachownicy będzie odpowiadał jeden wierzchołek, a krawędź będzie łączyła dwa wierzchołki, jeśli odpowiadające im pola sąsiadują (mają wspólny bok). Wierzchołki, tak jak pola szachownicy, możemy pomalować na biało i czarno. Zauważmy, że każda krawędź będzie łączyć wierzchołki różnych kolorów, zatem uzyskany przez nas graf będzie dwudzielny. Oznaczmy jego białe wierzchołki przez 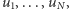 a czarne przez
a czarne przez 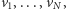 co więcej, ponumerujmy te wierzchołki kolejno wierszami i załóżmy, że liczba kolumn
co więcej, ponumerujmy te wierzchołki kolejno wierszami i załóżmy, że liczba kolumn  jest parzysta (co najmniej jedna z liczb
jest parzysta (co najmniej jedna z liczb 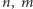 musi taka być).
musi taka być).
Graf dwudzielny możemy też opisać za pomocą zerojedynkowej macierzy dwusąsiedztwa 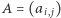 rozmiaru
rozmiaru 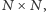 w której
w której 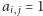 wtedy, gdy istnieje krawędź łącząca biały wierzchołek
wtedy, gdy istnieje krawędź łącząca biały wierzchołek 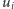 z czarnym wierzchołkiem
z czarnym wierzchołkiem 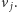 Przykładowo, dla szachownicy
Przykładowo, dla szachownicy  graf i jego macierz dwusąsiedztwa wyglądają następująco.
graf i jego macierz dwusąsiedztwa wyglądają następująco.
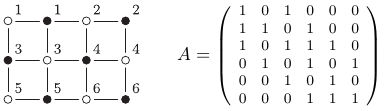
A czym w terminologii grafowej są pokrycia szachownicy kostkami domina? Otóż odpowiadają one doskonałym skojarzeniom, czyli takim zbiorom złożonym z 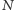 krawędzi grafu, że każdy wierzchołek jest incydentny z dokładnie jedną krawędzią z tego zbioru. Natomiast w macierzy dwusąsiedztwa odpowiadają one wybraniu
krawędzi grafu, że każdy wierzchołek jest incydentny z dokładnie jedną krawędzią z tego zbioru. Natomiast w macierzy dwusąsiedztwa odpowiadają one wybraniu 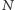 komórek z wartością 1, z których żadne dwie nie leżą w jednym wierszu ani w jednej kolumnie.
komórek z wartością 1, z których żadne dwie nie leżą w jednym wierszu ani w jednej kolumnie.
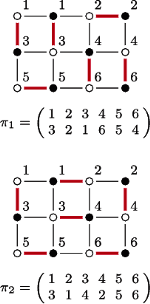
Rys. 2 Doskonałe skojarzenia (wyróżnione kolorem) w kracie  odpowiadające permutacjom
odpowiadające permutacjom 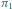 i
i 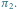
Aby wyznaczyć liczbę doskonałych skojarzeń, można rozważyć wszystkie przyporządkowania, które każdemu wierzchołkowi białemu przypisują pewien wierzchołek czarny połączony z nim krawędzią (przy czym każdy wierzchołek czarny musi być przypisany dokładnie jednemu wierzchołkowi białemu). Takie przyporządkowanie można zakodować za pomocą permutacji 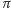 zbioru
zbioru 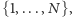 która wierzchołkowi
która wierzchołkowi 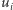 przypisuje wierzchołek
przypisuje wierzchołek 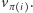 Wierzchołki te są połączone krawędzią, jeśli
Wierzchołki te są połączone krawędzią, jeśli 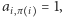 zatem przyporządkowanie jest poprawne, gdy iloczyn
zatem przyporządkowanie jest poprawne, gdy iloczyn 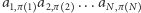 jest równy jeden (Rys. 2). Tak więc liczba doskonałych skojarzeń to po prostu permanent macierzy
jest równy jeden (Rys. 2). Tak więc liczba doskonałych skojarzeń to po prostu permanent macierzy  :
:
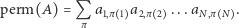 |
W krótkiej notatce O wieżach, permanencie i parzystości zamieszczonej w Delcie 10/2010 pisaliśmy już o tym, jak efektywnie obliczać parzystość permanentu macierzy całkowitoliczbowej przez porównanie go z wyznacznikiem tej samej macierzy. Wspomnieliśmy również, że problem obliczenia permanentu (a nie tylko jego parzystości) jest dużo trudniejszy i nie znamy dla niego szybszych algorytmów niż wykładnicze ze względu na 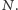 W szczególności oznacza to, że nie znamy lepszych algorytmów wyznaczania liczby doskonałych skojarzeń w dowolnych grafach dwudzielnych. Okazuje się jednak, że w przypadku specjalnego rodzaju grafu (kraty
W szczególności oznacza to, że nie znamy lepszych algorytmów wyznaczania liczby doskonałych skojarzeń w dowolnych grafach dwudzielnych. Okazuje się jednak, że w przypadku specjalnego rodzaju grafu (kraty 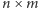 ), z którym mamy tu do czynienia, możemy to zrobić w czasie wielomianowym. I znowu pomoże nam w tym fakt, że umiemy efektywnie obliczać wyznacznik macierzy.
), z którym mamy tu do czynienia, możemy to zrobić w czasie wielomianowym. I znowu pomoże nam w tym fakt, że umiemy efektywnie obliczać wyznacznik macierzy.
Przypomnijmy, że wyznacznik również można zdefiniować w języku permutacji. Jest to analogiczna suma jak w przypadku permanentu, z tym że iloczyn odpowiadający permutacji 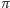 mnożymy teraz przez znak tej permutacji, który oznaczymy przez
mnożymy teraz przez znak tej permutacji, który oznaczymy przez 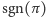 :
:
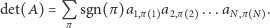 |
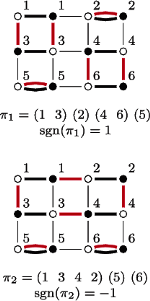
Rys. 3 Pokrycia cyklowe (wyróżnione pogrubionymi krawędziami) w kracie  odpowiadające permutacjom
odpowiadające permutacjom  i
i  oraz reprezentacja cyklowa i znaki tych permutacji.
oraz reprezentacja cyklowa i znaki tych permutacji.
Do zdefiniowania znaku permutacji przyda nam się pojęcie cyklu permutacji. Cyklem długości  nazwiemy ciąg indeksów
nazwiemy ciąg indeksów 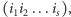 dla którego zachodzi
dla którego zachodzi 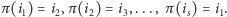 Każdą permutację możemy przedstawić w postaci zbioru rozłącznych cykli. Permutacja
Każdą permutację możemy przedstawić w postaci zbioru rozłącznych cykli. Permutacja 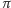 jest parzysta, a jej znak wynosi
jest parzysta, a jej znak wynosi 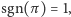 jeśli w jej rozkładzie na cykle występuje parzysta liczba cykli parzystej długości. W przeciwnym przypadku permutacja jest nieparzysta, a jej znak to
jeśli w jej rozkładzie na cykle występuje parzysta liczba cykli parzystej długości. W przeciwnym przypadku permutacja jest nieparzysta, a jej znak to 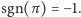
Jeśli w grafie wyróżnimy krawędzie doskonałego skojarzenia odpowiadającego permutacji  a także wszystkie krawędzie łączące pary wierzchołków o różnych kolorach, lecz tych samych numerach (tzn.
a także wszystkie krawędzie łączące pary wierzchołków o różnych kolorach, lecz tych samych numerach (tzn.  z
z  ), to każdy wierzchołek będzie incydentny z dokładnie dwiema krawędziami z wyróżnionego zbioru, zatem zbiór ten będzie pokryciem cyklowym grafu (czyli takim zbiorem rozłącznych cykli, że każdy wierzchołek należy do dokładnie jednego cyklu). Przy czym dopuszczamy, że niektóre krawędzie wyróżnimy dwukrotnie, co będzie odpowiadało trywialnym cyklom. Zapewne nie zdziwi nas, że każdy cykl długości
), to każdy wierzchołek będzie incydentny z dokładnie dwiema krawędziami z wyróżnionego zbioru, zatem zbiór ten będzie pokryciem cyklowym grafu (czyli takim zbiorem rozłącznych cykli, że każdy wierzchołek należy do dokładnie jednego cyklu). Przy czym dopuszczamy, że niektóre krawędzie wyróżnimy dwukrotnie, co będzie odpowiadało trywialnym cyklom. Zapewne nie zdziwi nas, że każdy cykl długości  z permutacji
z permutacji 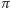 wyznacza pewien cykl długości
wyznacza pewien cykl długości 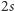 z pokrycia cyklowego (Rys. 3).
z pokrycia cyklowego (Rys. 3).
Jesteśmy już gotowi na przedstawienie błyskotliwego pomysłu, który pozwoli nam użyć algorytmu obliczania wyznacznika do obliczenia permanentu macierzy  Idea polega na takiej modyfikacji niezerowych elementów macierzy
Idea polega na takiej modyfikacji niezerowych elementów macierzy 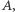 żeby dla każdej permutacji
żeby dla każdej permutacji 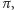 odpowiadającej doskonałemu skojarzeniu, iloczyn
odpowiadającej doskonałemu skojarzeniu, iloczyn  był równy 1, jeśli ta permutacja jest parzysta, oraz
był równy 1, jeśli ta permutacja jest parzysta, oraz 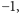 jeśli jest nieparzysta. Okazuje się, że aby to osiągnąć, wystarczy zastąpić jedynki występujące w komórkach macierzy
jeśli jest nieparzysta. Okazuje się, że aby to osiągnąć, wystarczy zastąpić jedynki występujące w komórkach macierzy 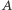 odpowiadających pionowym krawędziom kraty przez liczbę zespoloną
odpowiadających pionowym krawędziom kraty przez liczbę zespoloną 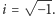 Oznaczmy tak uzyskaną macierz przez
Oznaczmy tak uzyskaną macierz przez 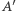 ; dla kraty
; dla kraty 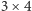 wygląda ona następująco.
wygląda ona następująco.

Przypatrzmy się, jaki wkład do iloczynu 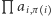 mają krawędzie z doskonałego skojarzenia odpowiadające ustalonemu cyklowi permutacji
mają krawędzie z doskonałego skojarzenia odpowiadające ustalonemu cyklowi permutacji  Jeśli oznaczymy liczność każdego z trzech rodzajów krawędzi, które mogą pojawić się na odpowiadającym mu cyklu w grafie, odpowiednio przez
Jeśli oznaczymy liczność każdego z trzech rodzajów krawędzi, które mogą pojawić się na odpowiadającym mu cyklu w grafie, odpowiednio przez 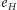 (poziome krawędzie ze skojarzenia),
(poziome krawędzie ze skojarzenia), 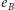 (poziome krawędzie nie ze skojarzenia) oraz
(poziome krawędzie nie ze skojarzenia) oraz 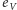 (pionowe krawędzie, zawsze pochodzące ze skojarzenia), to ten wkład będzie równy
(pionowe krawędzie, zawsze pochodzące ze skojarzenia), to ten wkład będzie równy  Przykładowy cykl wraz z licznościami krawędzi przedstawiono na rysunku 4. Zauważmy, że jeśli cykl ten ma długość 1, to odpowiada mu jedna pozioma krawędź (zatem wkład jest równy 1). Dalej zakładamy zatem, że cykl ten jest nietrywialny.
Przykładowy cykl wraz z licznościami krawędzi przedstawiono na rysunku 4. Zauważmy, że jeśli cykl ten ma długość 1, to odpowiada mu jedna pozioma krawędź (zatem wkład jest równy 1). Dalej zakładamy zatem, że cykl ten jest nietrywialny.
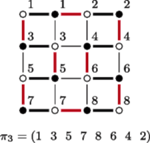
Rys. 4 Cykl w kracie  odpowiadający permutacji
odpowiadający permutacji 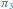 ma krawędzie:
ma krawędzie: 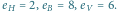
Aby obejść cykl w grafie i wrócić do punktu wyjścia, liczba pionowych krawędzi, którymi będziemy iść w dół, oraz liczba tych krawędzi, którymi będziemy iść w górę, muszą być równe. Zatem 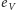 jest liczbą parzystą. Symetryczny argument dowodzi, że liczba
jest liczbą parzystą. Symetryczny argument dowodzi, że liczba 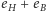 jest parzysta. Co więcej, z uwagi na rozmieszczenie krawędzi nie ze skojarzenia, każde przejście dwiema kolejnymi krawędziami powoduje albo zmianę numeru kolumny o 2 (gdy przechodzimy krawędziami
jest parzysta. Co więcej, z uwagi na rozmieszczenie krawędzi nie ze skojarzenia, każde przejście dwiema kolejnymi krawędziami powoduje albo zmianę numeru kolumny o 2 (gdy przechodzimy krawędziami  i
i 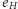 ), albo zmianę parzystości tej kolumny, ale tylko w obrębie pary kolumn, tzn.
), albo zmianę parzystości tej kolumny, ale tylko w obrębie pary kolumn, tzn. 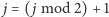 (gdy przechodzimy krawędziami
(gdy przechodzimy krawędziami 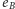 i
i 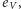 więc kolejna krawędź
więc kolejna krawędź 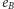 znajduje się tuż pod lub tuż nad poprzednią). Z tego wynika, że obu rodzajów przejść musi być parzyście wiele, zatem liczby
znajduje się tuż pod lub tuż nad poprzednią). Z tego wynika, że obu rodzajów przejść musi być parzyście wiele, zatem liczby 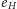 i
i 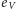 są parzyste. W konsekwencji parzysta jest też liczba
są parzyste. W konsekwencji parzysta jest też liczba 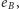 zatem w pokryciu cyklowym wszystkie nietrywialne cykle odpowiadają parzystym cyklom permutacji.
zatem w pokryciu cyklowym wszystkie nietrywialne cykle odpowiadają parzystym cyklom permutacji.

Przypatrzmy się kierunkom (lewo bądź prawo), w których poruszamy się poziomymi krawędziami, podczas obchodzenia cyklu w grafie. Każda zmiana kierunku odbywa się wtedy i tylko wtedy, gdy przechodzimy pionową krawędzią (znowu wynika to z faktu, że dwie kolejne krawędzie  na cyklu rozdzielone krawędzią
na cyklu rozdzielone krawędzią 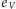 muszą znajdować się pod sobą). Wynika z tego, że wszystkimi poziomymi krawędziami leżącymi w wierszach o ustalonej parzystości będziemy przechodzić w tym samym kierunku. A ponieważ spośród wierszy kraty zawierających krawędzie z cyklu, pierwszy i ostatni musimy przejść w przeciwnych kierunkach (dlaczego?), więc muszą być one różnej parzystości. Jeśli podzielimy cykl na maksymalne kawałki niezawierające krawędzi z pierwszego i ostatniego wiersza, to dwa z tych kawałków (łączące różne wiersze) będą zawierały nieparzystą liczbę krawędzi
muszą znajdować się pod sobą). Wynika z tego, że wszystkimi poziomymi krawędziami leżącymi w wierszach o ustalonej parzystości będziemy przechodzić w tym samym kierunku. A ponieważ spośród wierszy kraty zawierających krawędzie z cyklu, pierwszy i ostatni musimy przejść w przeciwnych kierunkach (dlaczego?), więc muszą być one różnej parzystości. Jeśli podzielimy cykl na maksymalne kawałki niezawierające krawędzi z pierwszego i ostatniego wiersza, to dwa z tych kawałków (łączące różne wiersze) będą zawierały nieparzystą liczbę krawędzi 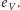 Jako ćwiczenie dla Czytelnika zostawiamy dowód faktu, że w pozostałych kawałkach (łączących ten sam wiersz) liczba krawędzi
Jako ćwiczenie dla Czytelnika zostawiamy dowód faktu, że w pozostałych kawałkach (łączących ten sam wiersz) liczba krawędzi 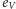 będzie podzielna przez 4. Z tego wynika, że liczba
będzie podzielna przez 4. Z tego wynika, że liczba 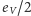 jest nieparzysta.
jest nieparzysta.
Skoro zatem 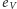 jest parzystą liczbą niepodzielną przez 4, to każdemu nietrywialnemu cyklowi permutacji odpowiada wartość
jest parzystą liczbą niepodzielną przez 4, to każdemu nietrywialnemu cyklowi permutacji odpowiada wartość  Ponieważ, jak pokazaliśmy wyżej, wszystkie nietrywialne cykle permutacji odpowiadającej doskonałemu skojarzeniu w kracie są długości parzystej, więc iloczyn
Ponieważ, jak pokazaliśmy wyżej, wszystkie nietrywialne cykle permutacji odpowiadającej doskonałemu skojarzeniu w kracie są długości parzystej, więc iloczyn 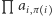 będzie równy
będzie równy 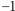 dokładnie wtedy, gdy będzie ich nieparzyście wiele (w przeciwnym przypadku będzie równy 1). Tak więc będzie on równy znakowi permutacji
dokładnie wtedy, gdy będzie ich nieparzyście wiele (w przeciwnym przypadku będzie równy 1). Tak więc będzie on równy znakowi permutacji 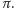 To pokazuje, że
To pokazuje, że  zatem
zatem
 |
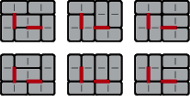
Rys. 5 Pokrycia szachownicy 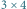 z dwiema zabronionymi krawędziami (wyróżnione kolorem).
z dwiema zabronionymi krawędziami (wyróżnione kolorem).
Warto wspomnieć, że jeśli w macierzy 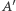 położymy
położymy 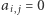 dla komórki, która odpowiada krawędzi łączącej wierzchołki
dla komórki, która odpowiada krawędzi łączącej wierzchołki 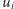 i
i 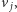 to
to 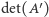 będzie liczbą tych doskonałych skojarzeń, które nie zawierają tej krawędzi. Odpowiadać to będzie takim układom kostek domina na szachownicy, w których żadna kostka nie przykrywa boku pomiędzy polami odpowiadającymi wierzchołkom
będzie liczbą tych doskonałych skojarzeń, które nie zawierają tej krawędzi. Odpowiadać to będzie takim układom kostek domina na szachownicy, w których żadna kostka nie przykrywa boku pomiędzy polami odpowiadającymi wierzchołkom 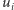 i
i 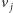 (Rys. 5).
(Rys. 5).
Łatwo zatem zaadaptować przedstawiony algorytm do liczenia przykryć "dziurawej" szachownicy (usunięcie pola z szachownicy symulujemy poprzez otoczenie go "murkiem" czterech zabronionych krawędzi) lub takich, w których część kostek ma już ustalone położenie.
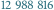 przykryć szachownicy rozmiaru
przykryć szachownicy rozmiaru 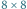 za pomocą 32 kostek domina.
za pomocą 32 kostek domina.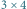 odpowiadające permutacjom
odpowiadające permutacjom 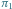 i
i 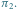
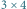 odpowiadające permutacjom
odpowiadające permutacjom 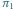 i
i 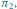 oraz reprezentacja cyklowa i znaki tych permutacji.
oraz reprezentacja cyklowa i znaki tych permutacji.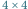 odpowiadający permutacji
odpowiadający permutacji 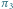 ma krawędzie:
ma krawędzie: 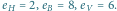
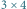 z dwiema zabronionymi krawędziami (wyróżnione kolorem).
z dwiema zabronionymi krawędziami (wyróżnione kolorem).