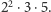Sieć światłowodowa
Tym razem omówimy zadanie Fiber-optic Network, które pojawiło się na zeszłorocznych zawodach ACM-ICPC Asia Mudanjiang Regional Contest.
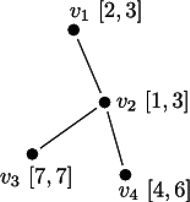
Dla 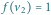 liczby w pozostałych trzech wierzchołkach możemy wybrać dowolnie, co daje 6 przyporządkowań
liczby w pozostałych trzech wierzchołkach możemy wybrać dowolnie, co daje 6 przyporządkowań 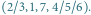 Dla
Dla 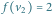 mamy jedno przyporządkowanie
mamy jedno przyporządkowanie 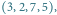 a dla
a dla 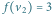 dwa
dwa 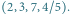 Odpowiedzi dla kolejnych wierzchołków to 22, 14, 63 i 44.
Odpowiedzi dla kolejnych wierzchołków to 22, 14, 63 i 44.
W zadaniu tym mamy dane drzewo o 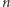 wierzchołkach, a dla każdego wierzchołka
wierzchołkach, a dla każdego wierzchołka  zadane liczby naturalne
zadane liczby naturalne 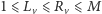 (ograniczenia to
(ograniczenia to 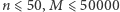 ). Dobrym przyporządkowaniem będziemy nazywać przyporządkowanie każdemu wierzchołkowi
). Dobrym przyporządkowaniem będziemy nazywać przyporządkowanie każdemu wierzchołkowi 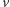 liczby całkowitej z odpowiadającego mu przedziału
liczby całkowitej z odpowiadającego mu przedziału ![|[Lv,Rv]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/6x-18e558cea23a4a7c8e2242994a14f32ef2d8c056-im-33,33,33-FF,FF,FF.gif) w taki sposób, aby liczby przyporządkowane wierzchołkom połączonym krawędzią były względnie pierwsze. Dla przejrzystości oznaczmy, że dla danego przyporządkowania
w taki sposób, aby liczby przyporządkowane wierzchołkom połączonym krawędzią były względnie pierwsze. Dla przejrzystości oznaczmy, że dla danego przyporządkowania 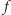 liczba przypisana wierzchołkowi
liczba przypisana wierzchołkowi  to
to 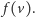 W zadaniu proszą nas, aby dla każdego wierzchołka obliczyć sumę liczb przyporządkowanych mu we wszystkich dobrych przyporządkowaniach. Wyniki należy podać modulo
W zadaniu proszą nas, aby dla każdego wierzchołka obliczyć sumę liczb przyporządkowanych mu we wszystkich dobrych przyporządkowaniach. Wyniki należy podać modulo 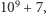 zatem wszystkie działania będziemy wykonywać modulo ta liczba.
zatem wszystkie działania będziemy wykonywać modulo ta liczba.
Chwila myślenia i odrobina algorytmicznego rozsądku doprowadzają nas do wniosku, że w zadaniu nie ma na tyle "regularności" (cokolwiek by to znaczyło), aby dało się rozwiązać je inaczej niż poprzez wyznaczenie dla każdego wierzchołka 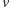 oraz każdej możliwej wartości
oraz każdej możliwej wartości 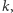 dla ilu dobrych przyporządkowań zachodzi
dla ilu dobrych przyporządkowań zachodzi 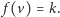 To właśnie będzie naszym celem.
To właśnie będzie naszym celem.
Jak można się spodziewać, zapewne sporo nam pomoże, jeżeli najpierw ukorzenimy nasze drzewo (w dowolnym wierzchołku). Rozwiązanie będzie bazowało na programowaniu dynamicznym. Oznaczymy przez 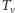 poddrzewo ukorzenione w wierzchołku
poddrzewo ukorzenione w wierzchołku 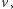 a przez
a przez ![dp[v][k]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/3x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) liczbę dobrych przyporządkowań, dla których zachodzi
liczbę dobrych przyporządkowań, dla których zachodzi 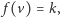 gdy ograniczymy się jedynie do wierzchołków z poddrzewa
gdy ograniczymy się jedynie do wierzchołków z poddrzewa 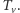 Niewątpliwie dla
Niewątpliwie dla  będących liśćmi zachodzi
będących liśćmi zachodzi ![dp[v][k] = 1,](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/7x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) gdy
gdy 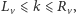 i
i ![|dp[v][k] = 0](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/9x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) dla pozostałych wartości
dla pozostałych wartości 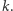 Załóżmy teraz, że chcemy wyznaczyć odpowiedź dla wierzchołka
Załóżmy teraz, że chcemy wyznaczyć odpowiedź dla wierzchołka 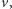 który ma
który ma  synów
synów 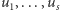 i mamy już wyznaczone tablice
i mamy już wyznaczone tablice ![|dp[u ],...,dp[u ]. 1 s](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/14x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) Liczba dobrych przyporządkowań dla poddrzewa
Liczba dobrych przyporządkowań dla poddrzewa 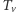 spełniających
spełniających 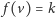 to iloczyn liczb dobrych przyporządkowań dla poddrzew
to iloczyn liczb dobrych przyporządkowań dla poddrzew 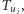 dla których
dla których 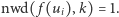 Zatem jeśli wprowadzimy oznaczenie
Zatem jeśli wprowadzimy oznaczenie
![P[u][k] = Q dp[u][j ] nwd k, j 1](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/19x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-dm-33,33,33-FF,FF,FF.gif) |
(zauważmy, że tak zapisana suma jest dobrze określona, gdyż tylko skończona liczba składników jest niezerowa), to dostaniemy wzór
![dp[v][k] = P [u1][k] ⋅...⋅P[us][k].](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/20x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-dm-33,33,33-FF,FF,FF.gif) |
(1) |
Moglibyśmy po prostu przeiterować po wszystkich możliwych wartościach 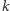 przyporządkowanych każdemu wierzchołkowi
przyporządkowanych każdemu wierzchołkowi 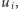 ale wtedy otrzymalibyśmy rozwiązanie co najmniej kwadratowe w zależności od
ale wtedy otrzymalibyśmy rozwiązanie co najmniej kwadratowe w zależności od 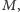 co byłoby zdecydowanie zbyt wolne. Dlatego stajemy przed kluczowym problemem szybkiego wyznaczenia
co byłoby zdecydowanie zbyt wolne. Dlatego stajemy przed kluczowym problemem szybkiego wyznaczenia ![P [u][k]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/24x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) dla ustalonego syna
dla ustalonego syna  Skoro mowa o względnej pierwszości, to z pewnością warto poznać zbiór (różnych) dzielników pierwszych liczby
Skoro mowa o względnej pierwszości, to z pewnością warto poznać zbiór (różnych) dzielników pierwszych liczby 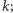 niech będą to liczby
niech będą to liczby 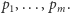 Liczby względnie pierwsze z
Liczby względnie pierwsze z 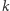 to wszystkie liczby poza tymi, które są podzielne przez którąkolwiek z liczb
to wszystkie liczby poza tymi, które są podzielne przez którąkolwiek z liczb 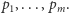 Dla
Dla 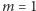 mamy
mamy ![|P[u][k] = P dp[u][j ] − P dp[u][j ], j p1S j](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/31x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) co umożliwia szybkie obliczenie żądanej wartości, o ile znalibyśmy wcześniej
co umożliwia szybkie obliczenie żądanej wartości, o ile znalibyśmy wcześniej ![Pp1S jdp[u][j ].](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/32x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) Życie nie jest jednak takie proste i w ogólnym przypadku nie możemy po prostu odjąć
Życie nie jest jednak takie proste i w ogólnym przypadku nie możemy po prostu odjąć ![PpiS jdp[u][ j]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/33x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) dla
dla 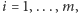 gdyż wiele ze składników postaci
gdyż wiele ze składników postaci ![|dp[u][ j]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/35x-2334bda81cf3c55e790ba7acf10d91088f7e72d0-im-33,33,33-FF,FF,FF.gif) odjęlibyśmy więcej niż raz (konkretnie tyle razy, ile
odjęlibyśmy więcej niż raz (konkretnie tyle razy, ile 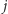 ma dzielników wśród liczb
ma dzielników wśród liczb 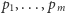 ).
).
Jeśli wprowadzimy oznaczenia 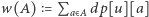 oraz
oraz 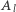 na zbiór liczb podzielnych przez liczbę
na zbiór liczb podzielnych przez liczbę 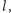 to dostaniemy zależność
to dostaniemy zależność
![P[u][k] = Q dp[u][j ] − w(Ap1 j](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/4x-29ea670833b65949ded28f8fee1981647dd86f36-dm-33,33,33-FF,FF,FF.gif) |
(2) |
Na ratunek w obliczeniu (2) przychodzi nam zasada włączeń i wyłączeń, a właściwie jej minimalne uogólnienie:
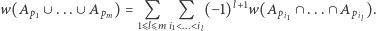 |
Pomimo przerażającego wyglądu wzór ten jest całkiem prosty, ale jeżeli ktoś nie spotkał się z nim wcześniej, warto się zatrzymać i pokontemplować go przez chwilę, np. przekonując się o jego poprawności dla 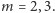 (Oczywiście, w ogólnej wersji wzoru nie ma znaczenia, czym są konkretnie zbiory
(Oczywiście, w ogólnej wersji wzoru nie ma znaczenia, czym są konkretnie zbiory 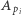 i pozostaje on prawdziwy dla dowolnych zbiorów.)
i pozostaje on prawdziwy dla dowolnych zbiorów.)
Zatem kolejną rzeczą, którą musimy zbadać, są zbiory postaci 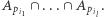 Wszystkie liczby
Wszystkie liczby 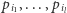 są pierwsze, więc jeżeli pewna liczba ma być podzielna przez wszystkie z nich, to musi być podzielna przez ich iloczyn (stwierdzenie odwrotne oczywiście też jest prawdziwe), co prowadzi nas do zależności
są pierwsze, więc jeżeli pewna liczba ma być podzielna przez wszystkie z nich, to musi być podzielna przez ich iloczyn (stwierdzenie odwrotne oczywiście też jest prawdziwe), co prowadzi nas do zależności
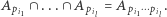
Dzięki niej wzór (2) możemy wyrazić następująco:
![P[u][k] = Q dp[u][ j] + Q Q (−1)ldp[u][ j]. j 1DlDm i1@...@il pi1⋯pilS j](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/4x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-dm-33,33,33-FF,FF,FF.gif) |
(3) |
Widać, że wielokrotnie spotykamy się tutaj z podobnymi sumami składników ![|dp[u][ j],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/5x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-im-33,33,33-FF,FF,FF.gif) zatem wprowadzając oznaczenie
zatem wprowadzając oznaczenie ![|S[u][i] = PiS jdp[u][j ],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/6x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-im-33,33,33-FF,FF,FF.gif) możemy przepisać wzór (3) w trochę milszej postaci:
możemy przepisać wzór (3) w trochę milszej postaci:
![P[u][k] = S[u][1] + Q Q (−1)lS[u][pi1⋯ pil]. 1DlDm i1@...@il](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/7x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-dm-33,33,33-FF,FF,FF.gif) |
(4) |
Zauważmy, że jeżeli mamy tablicę ![|dp[u],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/8x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-im-33,33,33-FF,FF,FF.gif) to jesteśmy w stanie relatywnie szybko wyznaczyć tablicę
to jesteśmy w stanie relatywnie szybko wyznaczyć tablicę ![S[u].](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/9x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-im-33,33,33-FF,FF,FF.gif) A konkretnie, aby obliczyć
A konkretnie, aby obliczyć ![|S[u][i],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/10x-38d7e2399b8ecd7eef9fd967ab164ac45d122502-im-33,33,33-FF,FF,FF.gif) potrzebujemy wysumować
potrzebujemy wysumować 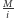 składników. Zatem wykonanie tego dla
składników. Zatem wykonanie tego dla 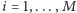 będzie miało złożoność czasową
będzie miało złożoność czasową

Zastanówmy się teraz, jaką złożoność ma wyznaczanie ![P [u][k]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/1x-6d50b56d9943e908c5f714f09f6751137a13451a-im-33,33,33-FF,FF,FF.gif) za pomocą wzoru (4). Zauważmy, że występują w nim jedynie składniki postaci
za pomocą wzoru (4). Zauważmy, że występują w nim jedynie składniki postaci ![|S[u][i],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/2x-6d50b56d9943e908c5f714f09f6751137a13451a-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 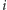 jest pewnym dzielnikiem
jest pewnym dzielnikiem 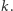 Ponadto nie wszystkie dzielniki uwzględniamy (tylko takie niepodzielne przez kwadraty liczb pierwszych), ale ta obserwacja nie jest nam potrzebna, aby uzyskać sensowne oszacowanie. Zatem, aby wyznaczyć wartości
Ponadto nie wszystkie dzielniki uwzględniamy (tylko takie niepodzielne przez kwadraty liczb pierwszych), ale ta obserwacja nie jest nam potrzebna, aby uzyskać sensowne oszacowanie. Zatem, aby wyznaczyć wartości ![P [u][k]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/5x-6d50b56d9943e908c5f714f09f6751137a13451a-im-33,33,33-FF,FF,FF.gif) dla
dla 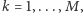 musimy wysumować co najwyżej tyle składników, ile jest łącznie dzielników liczb
musimy wysumować co najwyżej tyle składników, ile jest łącznie dzielników liczb 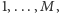 ale ich liczba jest również rzędu
ale ich liczba jest również rzędu 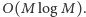 Aby szybko się dostać do tych składników, warto na samym początku programu dla każdej liczby od
Aby szybko się dostać do tych składników, warto na samym początku programu dla każdej liczby od 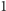 do
do 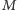 spamiętać jej bezkwadratowe dzielniki.
spamiętać jej bezkwadratowe dzielniki.
Podsumowując, mając tablice ![dp[ui]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/1x-8f18e519a89603943df1a33cf381025c19dbd2a2-im-33,33,33-FF,FF,FF.gif) dla wszystkich synów wierzchołka
dla wszystkich synów wierzchołka 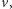 możemy w czasie
możemy w czasie 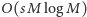 kolejno wyznaczyć tablice
kolejno wyznaczyć tablice ![|S[ui]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/4x-8f18e519a89603943df1a33cf381025c19dbd2a2-im-33,33,33-FF,FF,FF.gif) i
i ![|P[ui],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/5x-8f18e519a89603943df1a33cf381025c19dbd2a2-im-33,33,33-FF,FF,FF.gif) co pozwoli nam skorzystać ze wzoru (1) do wyznaczenia
co pozwoli nam skorzystać ze wzoru (1) do wyznaczenia ![|dp[v].](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/6x-8f18e519a89603943df1a33cf381025c19dbd2a2-im-33,33,33-FF,FF,FF.gif) Zatem w sumarycznym czasie
Zatem w sumarycznym czasie 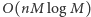 możemy tą metodą wyznaczyć odpowiedź dla korzenia drzewa. Uruchamiając powyższy algorytm dla każdej możliwości wyboru korzenia, możemy rozwiązać zadanie w czasie
możemy tą metodą wyznaczyć odpowiedź dla korzenia drzewa. Uruchamiając powyższy algorytm dla każdej możliwości wyboru korzenia, możemy rozwiązać zadanie w czasie 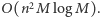 Jednak autorów zadania taka złożoność nie satysfakcjonuje i wymagane jest rozwiązanie
Jednak autorów zadania taka złożoność nie satysfakcjonuje i wymagane jest rozwiązanie 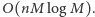
Pomysł pozwalający obliczać nam kompletne informacje dla wszystkich wierzchołków drzewa (a nie tylko te uwzględniające wierzchołki z odpowiadających im poddrzew), polega na spychaniu informacji z korzenia w dół, przesyłając informacje z "naddrzewa". Niech  będzie pewnym wierzchołkiem, a
będzie pewnym wierzchołkiem, a  jego ojcem w drzewie. Pamiętamy, że tablica
jego ojcem w drzewie. Pamiętamy, że tablica 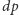 jest iloczynem odpowiednich wartości tablic
jest iloczynem odpowiednich wartości tablic 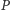 dla sąsiadów w poddrzewie, dlatego jeżeli mamy kompletną tablicę
dla sąsiadów w poddrzewie, dlatego jeżeli mamy kompletną tablicę ![dp[w], |](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/5x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) to aby obliczyć wkład naddrzewa
to aby obliczyć wkład naddrzewa  o korzeniu w wierzchołku
o korzeniu w wierzchołku 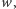 powinniśmy podzielić wartości z tablicy
powinniśmy podzielić wartości z tablicy ![|dp[w]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/8x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) przez odpowiadające wartości z tablicy
przez odpowiadające wartości z tablicy ![|P[v],](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/9x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) przeliczyć jeszcze raz wartości tablic
przeliczyć jeszcze raz wartości tablic ![|S[w]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/10x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) i
i ![P | [w]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/11x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) na podstawie nowych wartości
na podstawie nowych wartości ![|dp[w]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/12x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) (tablice te teraz lekko zmieniają swoje znaczenie, gdyż zmieniamy zbiór sąsiadów, którzy są uwzględniani w ich liczeniu), co pozwala nam wyliczyć kompletną tablicę
(tablice te teraz lekko zmieniają swoje znaczenie, gdyż zmieniamy zbiór sąsiadów, którzy są uwzględniani w ich liczeniu), co pozwala nam wyliczyć kompletną tablicę ![dp[v] |](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/13x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) (tzn. taką, w której uwzględniony jest też ojciec). Aby wyznaczyć kompletne
(tzn. taką, w której uwzględniony jest też ojciec). Aby wyznaczyć kompletne ![dp[v]](/math/temat/informatyka/algorytmy/2015/09/24/Siec_swiatlowodowa/14x-51057e2105665bafa6836f3c60bdf64913028f54-im-33,33,33-FF,FF,FF.gif) na podstawie informacji z ojca, potrzebujemy wykonać stałą liczbę przeliczeń tablic, z których każde odbywa się w czasie
na podstawie informacji z ojca, potrzebujemy wykonać stałą liczbę przeliczeń tablic, z których każde odbywa się w czasie 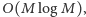 co daje algorytm o sumarycznej złożoności
co daje algorytm o sumarycznej złożoności 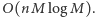
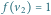 liczby w pozostałych trzech wierzchołkach możemy wybrać dowolnie, co daje 6 przyporządkowań
liczby w pozostałych trzech wierzchołkach możemy wybrać dowolnie, co daje 6 przyporządkowań 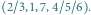 Dla
Dla 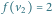 mamy jedno przyporządkowanie
mamy jedno przyporządkowanie 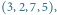 a dla
a dla 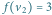 dwa
dwa 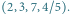 Odpowiedzi dla kolejnych wierzchołków to 22, 14, 63 i 44.
Odpowiedzi dla kolejnych wierzchołków to 22, 14, 63 i 44.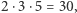 to musimy dodać liczby podzielne przez
to musimy dodać liczby podzielne przez 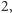 przez
przez 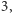 przez
przez 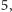 odjąć liczby podzielne przez
odjąć liczby podzielne przez 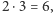 przez
przez 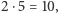 przez
przez 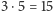 i dodać liczby podzielne przez
i dodać liczby podzielne przez 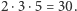 Warto też zauważyć, że potęgi, w których dane liczby pierwsze dzielą
Warto też zauważyć, że potęgi, w których dane liczby pierwsze dzielą 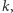 nie mają żadnego znaczenia - liczby względnie pierwsze z
nie mają żadnego znaczenia - liczby względnie pierwsze z 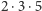 to te same liczby, co liczby względnie pierwsze z
to te same liczby, co liczby względnie pierwsze z