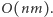Informatyczny kącik olimpijski

Sklep ze słodyczami

Tym razem zadanie Candies z Bałtyckiej Olimpiady Informatycznej z 2010 roku.

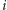Zadanie. W sklepie znajduje się $|n$ paczek z cukierkami, $i$ -ta z nich zawiera 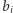$bi$ cukierków. Sklepikarz może sprzedawać jedynie całe paczki, więc jeśli w sklepie są cztery paczki zawierające 1, 3, 4 i 4 cukierki, to może on obsłużyć następnego klienta tylko wtedy, gdy ten złoży zamówienie jednego z 9 rozmiarów (konkretnie gdy poprosi o 1, 3, 4, 5, 7, 8, 9, 11 lub 12 cukierków). Sklepikarz zastanawia się, jak bardzo mógłby zwiększyć liczbę możliwości, gdyby zamienił liczbę cukierków w jednej z paczek. Przykładowo, po wyrzuceniu jednej paczki z 4 cukierkami i dodaniu paczki z 9 cukierkami, liczba możliwych do zrealizowania zamówień zwiększy się do 13 (będą to 1, 3, 4, 5, 7, 8, 9, 10, 12, 13, 14, 16, 17). Jeśli istnieje więcej niż jedno optymalne rozwiązanie, w którym sklepikarz zamienia paczkę z 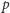$|p$ cukierkami na paczkę z 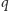$|q$ cukierkami, należy podać to, w którym para 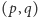$(p,q)$ jest minimalna leksykograficznie.

Załóżmy na początek, że wyrzuciliśmy którąś z paczek, a zestaw pozostałych 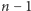$n − 1$ paczek umożliwia zrealizowanie zamówień o wielkościach 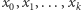$x0,x1,...,xk$ (zakładamy przy tym, że zamówienie 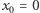$|x0 = 0$ również jest poprawne). Jeśli dodamy do tego zestawu paczkę 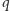$|q$ cukierków, to będziemy mogli dodatkowo zrealizować zamówienia 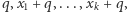$|q,x + q,...,x + q, 1 k$ a zatem jeśli 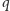$|q$ nie jest równe żadnej różnicy $|xi− x j,$ to liczba zamówień wzrośnie dwukrotnie. Możemy to sobie zagwarantować, dodając wystarczająco dużą paczkę, np. 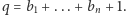rozmiaru $|q = b1 + ...+ bn + 1.$ Rozwiązanie zadania można zatem podzielić na dwie części: znalezienie paczki 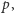$p,$ której wyrzucenie jak najmniej zmniejszy liczbę możliwych zamówień, oraz znalezienie jak najmniejszej paczki 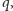$|q,$ która spowoduje dwukrotne zwiększenie liczby możliwych zamówień.

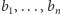Zadanie to jest pewną wariacją na temat problemu plecakowego (o którym pisaliśmy m.in. w numerze 6/2013). W szczególności wyznaczenie liczby zamówień możliwych do zrealizowania przez początkowy zestaw paczek to zastosowanie tego algorytmu do $n$ przedmiotów rozmiarów $|b1,...,bn$ i plecaka o udźwigu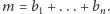 $|m = b1 + ...+ bn.$

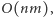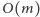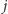Pseudokod algorytmu znajduje się obok. Przypomnijmy istotne dla nas kwestie: czas działania algorytmu wynosi $|O(nm),$ analizuje on przedmioty pojedynczo (w czasie $O(m)$ każdy), aktualizując tablicę $d[0..m]$ (w wynikowej tablicy mamy $|d[ j] = 1,$ jeśli zamówienie rozmiaru $j$ może być zrealizowane), oraz dla ostatecznego wyniku nie ma znaczenia kolejność, w której przedmioty są analizowane. Możemy abstrahować od szczegółów implementacyjnych i zamknąć go w strukturze danych, która w czasie 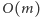$|O(m)$ będzie umożliwiała wykonywanie trzech operacji: zrobienie kopii struktury, dodanie nowego przedmiotu oraz wyznaczenie liczby zamówień realizowanych przez dodane przedmioty.

Aby znaleźć paczkę 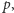$|p,$ potrzebujemy rozwiązać problem plecakowy dla każdego podzbioru 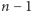$n −1$ przedmiotów. Jeśli rozpatrzymy każdy z tych podzbiorów niezależnie, dostaniemy algorytm o złożoności czasowej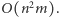 $|O(n2m).$

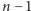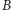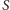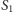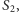Możemy postąpić nieco sprytniej. Będziemy utrzymywać listę struktur danych (na początek zaczynamy z jedną pustą strukturą danych). 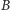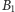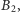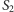Teraz, dopóki struktury na liście zawierają mniej niż $|n− 1$ przedmiotów, to dla każdej struktury $B$ dzielimy zbiór przedmiotów $S$ niewystępujących w tej strukturze na dwa w miarę równe podzbiory $|S1$ i $|S2,$ a strukturę $B$ zastępujemy jej kopiami $|B1$ i $|B2,$ do których dodajemy przedmioty odpowiednio z podzbiorów $S1$ i $S2$ (patrz rysunek). Jeśli dla uproszczenia założymy, że 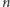$|n$ jest potęgą dwójki, to w 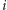$i$ -tej fazie tego algorytmu wygenerujemy 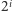$i |2$ struktur, do każdej z nich dodając 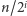$i n/2$ przedmiotów. Zatem złożoność czasowa każdej z 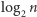$log2n$ faz wyniesie 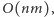$|O(nm),$ czyli rozwiązanie problemu plecakowego dla wszystkich podzbiorów 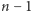$n − 1$ przedmiotów zajmie czas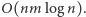 $O(nm log n).$

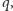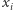Pozostaje teraz znalezienie minimalnej liczby $|q,$ która nie będzie równa żadnej różnicy $x − x . i j$ Ponieważ $x i$ są zamówieniami generowanymi przez wybrany podzbiór 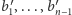$′ ′ b 1,...,bn−1$ paczek, to wszystkie różnice będą generowane przez zbiór 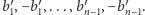$|b′1,− b′1,...,b′n−1,−b′n−1.$ Wystarczy zatem rozwiązać problem plecakowy dla takich przedmiotów (w naszej wersji tego problemu przedmioty o ujemnym rozmiarze nie stanowią problemu, należy jednak zwrócić uwagę na rozmiar tablicy i poprawną kolejność pętli) i zwrócić jako 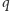$|q$ minimalną dodatnią liczbę, dla której $d[ j] = 0.$ Czas działania tej części rozwiązania to $O(nm).$