Informatyczny kącik olimpijski
Więzienie
Dzisiejsze zadanie pochodzi z VII obozu informatycznego ILOCAMP.
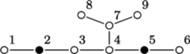
rys1 Przykładowe drzewo 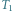 o
o 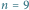 wierzchołkach i wyróżnionym zbiorze
wierzchołkach i wyróżnionym zbiorze 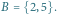 Mamy tu dwa minimalne zbiory blokujące:
Mamy tu dwa minimalne zbiory blokujące: 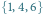 i
i 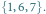
Zadanie. Więzienie składa się z 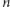 cel i
cel i 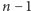 łączących je korytarzy. W części z cel znajdują się więźniowie. Reszta cel jest pusta. W wyniku awarii wszystkie cele zostały otwarte. Jaka jest minimalna liczba strażników potrzebnych do uniemożliwienia więźniom ucieczki? Strażników można rozmieszczać jedynie w pustych celach, a więzień może uciec, jeśli na drodze od jego celi do celi wyjściowej (takiej, do której prowadzi tylko jeden korytarz) nie ma żadnej celi ze strażnikiem.
łączących je korytarzy. W części z cel znajdują się więźniowie. Reszta cel jest pusta. W wyniku awarii wszystkie cele zostały otwarte. Jaka jest minimalna liczba strażników potrzebnych do uniemożliwienia więźniom ucieczki? Strażników można rozmieszczać jedynie w pustych celach, a więzień może uciec, jeśli na drodze od jego celi do celi wyjściowej (takiej, do której prowadzi tylko jeden korytarz) nie ma żadnej celi ze strażnikiem.
Zadanie można przeformułować następująco: dane jest  -wierzchołkowe drzewo, w którym wyróżniono podzbiór wierzchołków
-wierzchołkowe drzewo, w którym wyróżniono podzbiór wierzchołków 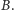 Należy znaleźć najmniejszy blokujący zbiór wierzchołków (rozłączny z
Należy znaleźć najmniejszy blokujący zbiór wierzchołków (rozłączny z 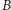 ), taki że każda ścieżka z dowolnego wierzchołka zbioru
), taki że każda ścieżka z dowolnego wierzchołka zbioru 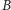 do dowolnego liścia drzewa musi przechodzić przez co najmniej jeden wierzchołek ze zbioru blokującego (patrz drzewo
do dowolnego liścia drzewa musi przechodzić przez co najmniej jeden wierzchołek ze zbioru blokującego (patrz drzewo 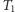 na rysunku 1).
na rysunku 1).
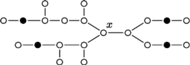
Rys. 2 Drzewo 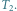 Minimalny zbiór blokujący ma 7 wierzchołków.
Minimalny zbiór blokujący ma 7 wierzchołków.
Na początek wypróbujmy kilku kandydatów na zbiór blokujący. Oczywiste jest, że zbiór wszystkich liści w drzewie jest zbiorem blokującym (zakładamy, że 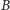 nie zawiera liścia, w przeciwnym przypadku zbiór blokujący nie istnieje). Również jest nim zbiór wszystkich niewyróżnionych sąsiadów wierzchołków z
nie zawiera liścia, w przeciwnym przypadku zbiór blokujący nie istnieje). Również jest nim zbiór wszystkich niewyróżnionych sąsiadów wierzchołków z 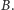 Dość łatwo się jednak przekonać, że żaden z nich nie musi być minimalny - dla drzewa
Dość łatwo się jednak przekonać, że żaden z nich nie musi być minimalny - dla drzewa 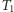 są to zbiory
są to zbiory 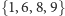 oraz
oraz 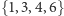 ; oba mają po 4 wierzchołki.
; oba mają po 4 wierzchołki.
Zacznijmy jednak od zbioru liści i spróbujmy usunąć z niego nadmiarowe wierzchołki. Jeśli jedyny sąsiad  liścia
liścia 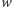 należy do zbioru
należy do zbioru 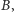 to każdy zbiór blokujący musi zawierać liść
to każdy zbiór blokujący musi zawierać liść 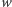 (np. każdy zbiór blokujący dla drzewa
(np. każdy zbiór blokujący dla drzewa 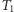 musi zawierać wierzchołki 1 i 6). Z drugiej strony, jeśli wierzchołek
musi zawierać wierzchołki 1 i 6). Z drugiej strony, jeśli wierzchołek  nie należy do
nie należy do 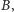 to istnieje minimalny zbiór blokujący, który nie zawiera liścia
to istnieje minimalny zbiór blokujący, który nie zawiera liścia 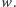 Jest tak dlatego, że każda ścieżka z
Jest tak dlatego, że każda ścieżka z 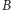 do
do 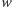 przechodzi przez
przechodzi przez 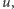 więc, blokując wierzchołek
więc, blokując wierzchołek  zamiast wierzchołka
zamiast wierzchołka 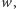 dostajemy równie dobre rozwiązanie. Postępując w ten sposób z drzewem
dostajemy równie dobre rozwiązanie. Postępując w ten sposób z drzewem 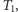 pozbędziemy się liści i znajdziemy zbiór blokujący
pozbędziemy się liści i znajdziemy zbiór blokujący 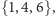 ale nie dla każdego drzewa tak znaleziony zbiór będzie minimalny (patrz drzewo
ale nie dla każdego drzewa tak znaleziony zbiór będzie minimalny (patrz drzewo 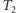 na rysunku 2).
na rysunku 2).
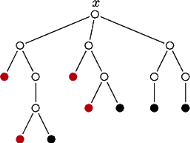
Rys. 3 Jedyna składowa drzewa 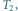 ukorzeniona w
ukorzeniona w 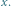 Wierzchołki z
Wierzchołki z 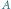 zaznaczone zostały kolorem, wierzchołki z
zaznaczone zostały kolorem, wierzchołki z 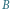 są czarne.
są czarne.
Zwodnicze jest, że w treści zadania liście oraz wyróżnione wierzchołki pełnią nieco inną rolę (w szczególności można blokować liście, ale nie wierzchołki z 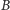 ). Możemy jednak nieznacznie przeformułować treść zadania, aby te role stały się w pełni symetryczne. Zauważyliśmy już, że musimy blokować jedynie liście sąsiadujące z
). Możemy jednak nieznacznie przeformułować treść zadania, aby te role stały się w pełni symetryczne. Zauważyliśmy już, że musimy blokować jedynie liście sąsiadujące z 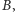 a ponieważ nie wpływają one na resztę wierzchołków, możemy je dodać do zbioru blokującego i usunąć z drzewa. Następnie oznaczmy zbiór pozostałych liści przez
a ponieważ nie wpływają one na resztę wierzchołków, możemy je dodać do zbioru blokującego i usunąć z drzewa. Następnie oznaczmy zbiór pozostałych liści przez 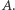 Składową w drzewie nazwiemy maksymalny zbiór wierzchołków, z których każde dwa można połączyć ścieżką, której wewnętrzne wierzchołki nie należą do zbioru
Składową w drzewie nazwiemy maksymalny zbiór wierzchołków, z których każde dwa można połączyć ścieżką, której wewnętrzne wierzchołki nie należą do zbioru 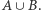 Przykładowo w drzewie
Przykładowo w drzewie 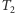 mamy jedną składową zawierającą 17 wierzchołków, a gdyby wierzchołek
mamy jedną składową zawierającą 17 wierzchołków, a gdyby wierzchołek 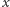 należał do
należał do 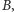 to mielibyśmy trzy składowe, o licznościach 6, 6 i 7. Zauważmy, że zbiór blokujący możemy wyznaczyć dla każdej składowej niezależnie. Będzie to taki podzbiór wierzchołków spoza
to mielibyśmy trzy składowe, o licznościach 6, 6 i 7. Zauważmy, że zbiór blokujący możemy wyznaczyć dla każdej składowej niezależnie. Będzie to taki podzbiór wierzchołków spoza 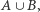 że każda ścieżka ze zbioru
że każda ścieżka ze zbioru 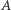 do zbioru
do zbioru 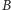 musi przecinać ten podzbiór.
musi przecinać ten podzbiór.
Weźmy zatem składową i ukorzeńmy ją w dowolnym wierzchołku spoza 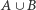 (Rys. 3). Zastosujemy teraz programowanie dynamiczne - przeglądając drzewo składowej od liści do korzenia, w każdym poddrzewie będziemy konstruować minimalny zbiór blokujący. Jednocześnie każdy wierzchołek
(Rys. 3). Zastosujemy teraz programowanie dynamiczne - przeglądając drzewo składowej od liści do korzenia, w każdym poddrzewie będziemy konstruować minimalny zbiór blokujący. Jednocześnie każdy wierzchołek 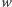 będziemy wrzucać do jednego z trzech zbiorów:
będziemy wrzucać do jednego z trzech zbiorów: 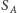 (jeśli poddrzewo zaczepione w
(jeśli poddrzewo zaczepione w 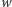 zawiera taki wierzchołek z
zawiera taki wierzchołek z 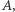 do którego ścieżka z
do którego ścieżka z  nie zawiera zablokowanych wierzchołków),
nie zawiera zablokowanych wierzchołków), 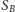 (poddrzewo to zawiera niezablokowany wierzchołek z
(poddrzewo to zawiera niezablokowany wierzchołek z 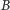 ) oraz
) oraz 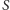 (wszystkie wierzchołki z
(wszystkie wierzchołki z 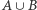 w tym poddrzewie są zablokowane - być może z powodu dodania wierzchołka
w tym poddrzewie są zablokowane - być może z powodu dodania wierzchołka 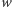 do zbioru blokującego).
do zbioru blokującego).
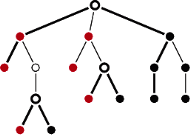
Rys. 4 Wierzchołki składowej przydzielone do zbiorów 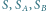 zaznaczone są odpowiednio na biało, kolorowo i czarno. Wyróżniono również wierzchołki minimalnego zbioru blokującego oraz odpowiadające im ścieżki.
zaznaczone są odpowiednio na biało, kolorowo i czarno. Wyróżniono również wierzchołki minimalnego zbioru blokującego oraz odpowiadające im ścieżki.
Wierzchołki ze zbiorów 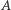 i
i 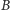 lądują odpowiednio w zbiorach
lądują odpowiednio w zbiorach 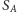 i
i 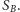 Rozważmy teraz wierzchołek wewnętrzny
Rozważmy teraz wierzchołek wewnętrzny  ; jeśli ma on takie dwoje dzieci, z których jedno należy do
; jeśli ma on takie dwoje dzieci, z których jedno należy do 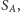 a drugie należy do
a drugie należy do 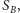 to przez wierzchołek
to przez wierzchołek 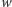 przechodzi (co najmniej jedna) niezablokowana ścieżka
przechodzi (co najmniej jedna) niezablokowana ścieżka 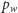 łącząca pewien wierzchołek z
łącząca pewien wierzchołek z 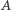 z pewnym wierzchołkiem z
z pewnym wierzchołkiem z 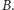 Dodajemy zatem
Dodajemy zatem 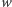 do zbioru blokującego oraz do zbioru
do zbioru blokującego oraz do zbioru 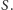 W przeciwnym przypadku wszystkie dzieci
W przeciwnym przypadku wszystkie dzieci 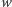 należą do zbioru
należą do zbioru 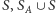 lub
lub 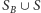 i dodajemy wierzchołek
i dodajemy wierzchołek 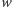 odpowiednio do zbioru
odpowiednio do zbioru 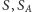 lub
lub 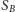 (Rys. 4).
(Rys. 4).
Jasne jest, że w ten sposób skonstruujemy poprawny zbiór blokujący 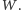 Dowodem na jego minimalność jest skonstruowany, niejako przy okazji, zbiór ścieżek
Dowodem na jego minimalność jest skonstruowany, niejako przy okazji, zbiór ścieżek 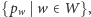 które są rozłączne, a każda musi zawierać co najmniej jeden wierzchołek z
które są rozłączne, a każda musi zawierać co najmniej jeden wierzchołek z 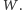 Złożoność czasowa rozwiązania to
Złożoność czasowa rozwiązania to 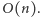
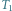 o
o 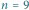 wierzchołkach i wyróżnionym zbiorze
wierzchołkach i wyróżnionym zbiorze 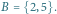 Mamy tu dwa minimalne zbiory blokujące:
Mamy tu dwa minimalne zbiory blokujące: 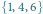 i
i 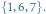
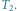 Minimalny zbiór blokujący ma 7 wierzchołków.
Minimalny zbiór blokujący ma 7 wierzchołków.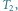 ukorzeniona w
ukorzeniona w 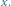 Wierzchołki z
Wierzchołki z 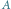 zaznaczone zostały kolorem, wierzchołki z
zaznaczone zostały kolorem, wierzchołki z 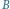 są czarne.
są czarne.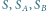 zaznaczone są odpowiednio na biało, kolorowo i czarno. Wyróżniono również wierzchołki minimalnego zbioru blokującego oraz odpowiadające im ścieżki.
zaznaczone są odpowiednio na biało, kolorowo i czarno. Wyróżniono również wierzchołki minimalnego zbioru blokującego oraz odpowiadające im ścieżki.