Informatyczny kącik olimpijski
Wiercenia
W tym kąciku omówimy zadanie Wiercenia, które pojawiło się na Potyczkach Algorytmicznych w roku 2009.

Ekipa poszukująca złóż ropy wykonała dwa odwierty: w punkcie 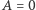 natrafiono na ropę, zaś w punkcie
natrafiono na ropę, zaś w punkcie 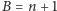 ropy nie znaleziono. Wiedząc, że złoże ropy zajmuje pewien spójny fragment odcinka
ropy nie znaleziono. Wiedząc, że złoże ropy zajmuje pewien spójny fragment odcinka 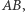 ekipa chce zlokalizować najdalszy punkt spośród punktów o współrzędnych
ekipa chce zlokalizować najdalszy punkt spośród punktów o współrzędnych 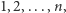 w którym występuje ropa. Wykonanie odwiertu w punkcie
w którym występuje ropa. Wykonanie odwiertu w punkcie 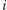 zajmuje czas
zajmuje czas ![|t[i]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/6x-24c6ff0a5bd2180267ac8f650d3e400619b6753a-im-33,33,33-FF,FF,FF.gif) ; ekipa może wykonywać tylko jeden odwiert naraz. Należy wyznaczyć taki plan wierceń, aby czas potrzebny na ustalenie, dokąd sięga złoże ropy, był w pesymistycznym przypadku jak najkrótszy.
; ekipa może wykonywać tylko jeden odwiert naraz. Należy wyznaczyć taki plan wierceń, aby czas potrzebny na ustalenie, dokąd sięga złoże ropy, był w pesymistycznym przypadku jak najkrótszy.
Na początek zauważmy, że jeśli wykonanie każdego z odwiertów zajmuje taki sam czas, to wtedy, stosując wyszukiwanie binarne, uzyskamy odpowiedź, wykonując optymalną liczbę 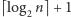 odwiertów. Zróżnicowanie czasów istotnie komplikuje zadanie; spróbujemy je rozwiązać, korzystając z programowania dynamicznego.
odwiertów. Zróżnicowanie czasów istotnie komplikuje zadanie; spróbujemy je rozwiązać, korzystając z programowania dynamicznego.
Oznaczmy przez ![d[a, b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/1x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) optymalny czas lokalizacji granicy złoża na odcinku od punktu
optymalny czas lokalizacji granicy złoża na odcinku od punktu  do punktu
do punktu 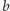 (włącznie), przy założeniu, że wiemy, iż w punkcie
(włącznie), przy założeniu, że wiemy, iż w punkcie 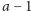 jest ropa, a w punkcie
jest ropa, a w punkcie 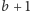 jej nie ma. Aby wyznaczyć granicę złoża na odcinku
jej nie ma. Aby wyznaczyć granicę złoża na odcinku ![|[a, b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/6x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) musimy zacząć od wykonania odwiertu w jednym z punktów
musimy zacząć od wykonania odwiertu w jednym z punktów 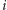 tego odcinka. Jeśli znajduje się tam ropa, to granicy złoża będziemy poszukiwać na odcinku
tego odcinka. Jeśli znajduje się tam ropa, to granicy złoża będziemy poszukiwać na odcinku ![[i + 1,b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/8x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) w przeciwnym przypadku granica jest na odcinku
w przeciwnym przypadku granica jest na odcinku ![[a,i −1].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/9x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) Dostajemy zatem wzór rekurencyjny
Dostajemy zatem wzór rekurencyjny
![d[a,b] = minaDi Db(t[i]+ max(d[a, i− 1],d[i + 1,b])).](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/10x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif) |
(*) |
Zakładamy, że ![d[a, b] = 0](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/11x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) dla
dla  Rozwiązaniem jest wartość
Rozwiązaniem jest wartość ![|d[1,n].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/13x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) Obliczenie jej wprost z powyższej rekurencji da nam algorytm o złożoności czasowej
Obliczenie jej wprost z powyższej rekurencji da nam algorytm o złożoności czasowej 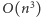 i pamięciowej
i pamięciowej 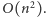 Algorytm będzie miał
Algorytm będzie miał  faz, w
faz, w 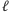 -tej fazie będziemy wypełniać komórki tablicy odpowiadające odcinkom o długości
-tej fazie będziemy wypełniać komórki tablicy odpowiadające odcinkom o długości 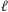 :
:
![for ℓ = 0to n −1 do fora = 1to n −ℓ do b = a + ℓ;d[a, b] = ∞ ; fori = a to b do d[a, b] = min(d[a, b],t[i] +max(d[a, i− 1],d[i + 1,b]));](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/19x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif)
Aby przyspieszyć powyższy algorytm, będziemy potrzebowali kilku obserwacji. Zauważmy, że jeśli przedłużymy jakiś odcinek, to czas szukania w nim granicy złoża jest zawsze nie mniejszy niż w oryginalnym odcinku. Zatem wraz ze wzrostem 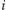 we wzorze
we wzorze 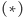 wartość
wartość ![| d[a,i− 1]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/22x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) nie zmniejsza się, a wartość
nie zmniejsza się, a wartość ![| d[i +1,b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/23x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) nie rośnie. Istnieje więc taki indeks
nie rośnie. Istnieje więc taki indeks ![|s[a, b]∈ [a− 1,b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/24x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) że spełnione są nierówności
że spełnione są nierówności
![d[a,i−1] ⩽d[i+1,b] dla i ⩽s[a,b] oraz d[a,i− 1] > d[i+1,b] dla i > s[a, b].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/25x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif)
Możemy zatem przepisać wzór 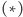 w równoważnej formie, pozbywając się liczenia maksimum:
w równoważnej formie, pozbywając się liczenia maksimum:
![d[a,b] = min (minaDi Ds a,b (t[i]+ d[i + 1,b]),mins a,b @i Db(t[i]+ d[a,i− 1])).](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/27x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif) |
(**) |
Skorzystamy również z tego, że tablica  jest monotoniczna względem każdej współrzędnej, dzięki czemu wartość
jest monotoniczna względem każdej współrzędnej, dzięki czemu wartość ![|s[a,b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/29x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) jest ograniczona przez wartości dla krótszych odcinków:
jest ograniczona przez wartości dla krótszych odcinków:
![s[a,b − 1]⩽ s[a, b]⩽ s[a +1,b].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/30x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif)
Istotnie, jeśli weźmiemy dowolne ![i⩽ s[a,b −1]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/31x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) i znowu skorzystamy z tego, że przedłużenie odcinka nie zmniejsza czasu poszukiwania granicy złoża, to dostaniemy
i znowu skorzystamy z tego, że przedłużenie odcinka nie zmniejsza czasu poszukiwania granicy złoża, to dostaniemy ![d[a, i− 1] ⩽ d[i + 1,b − 1]⩽ d[i + 1,b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/32x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) zatem
zatem ![|i⩽ s[a, b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/33x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) co dowodzi lewej nierówności (prawej dowodzimy analogicznie). Ponieważ
co dowodzi lewej nierówności (prawej dowodzimy analogicznie). Ponieważ ![s[a,a] = a,](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/34x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) to możemy dla wygody przyjąć
to możemy dla wygody przyjąć ![s[a,b] = b](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/35x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) dla
dla 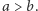 Zatem, aby wyznaczyć
Zatem, aby wyznaczyć ![|s[a, b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/37x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) wystarczy przejrzeć wartości od
wystarczy przejrzeć wartości od ![s[a,b −1]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/38x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) do
do ![s[a+ 1,b].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/39x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) Dzięki temu wyznaczenie ich dla wszystkich odcinków
Dzięki temu wyznaczenie ich dla wszystkich odcinków ![s[a,a + ℓ]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/40x-e61fd52f612df379634bb6066e865c487a205dc1-im-33,33,33-FF,FF,FF.gif) o ustalonej długości
o ustalonej długości 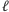 zajmie sumarycznie czas liniowy:
zajmie sumarycznie czas liniowy:
![n−ℓ (s[a +1,a + ℓ]+ 1− s[a, a+ ℓ −1]) = s[n − ℓ+ 1,n]− s[1,ℓ] +n − ℓ ⩽2n. Qa 1](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/42x-e61fd52f612df379634bb6066e865c487a205dc1-dm-33,33,33-FF,FF,FF.gif)
W końcu pokażemy, jak szybko wyliczać minima we wzorze 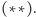 Załóżmy, że mamy strukturę danych, która przechowuje pary (indeks, wartość) i udostępnia operacje jak na kolejce: wstawienie pary na koniec kolejki (push) oraz usunięcie pary z początku kolejki (pop). Dodatkowo operacja first będzie zwracać indeks pary z początku kolejki, a kluczowa operacja min będzie zwracała minimum ze wszystkich wartości w kolejce. Będziemy korzystać z
Załóżmy, że mamy strukturę danych, która przechowuje pary (indeks, wartość) i udostępnia operacje jak na kolejce: wstawienie pary na koniec kolejki (push) oraz usunięcie pary z początku kolejki (pop). Dodatkowo operacja first będzie zwracać indeks pary z początku kolejki, a kluczowa operacja min będzie zwracała minimum ze wszystkich wartości w kolejce. Będziemy korzystać z 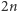 kolejek, które nazwiemy
kolejek, które nazwiemy ![A[i]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/3x-d4b06dc2a29b2ee235c8e2280f021f8434b97694-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![|B[i]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/4x-d4b06dc2a29b2ee235c8e2280f021f8434b97694-im-33,33,33-FF,FF,FF.gif) dla
dla 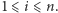
Podczas wyliczania ![d[a,b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/1x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) w
w 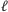 -tej fazie algorytmu będziemy zakładać, że wszystkie wartości z lewego minimum w
-tej fazie algorytmu będziemy zakładać, że wszystkie wartości z lewego minimum w 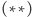 znajdują się w kolejce
znajdują się w kolejce ![B[b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/4x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) (w kolejności malejących indeksów
(w kolejności malejących indeksów 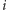 ), a wszystkie wartości z prawego minimum w kolejce
), a wszystkie wartości z prawego minimum w kolejce ![A[a]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/6x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) (w kolejności rosnących indeksów). Kolejka
(w kolejności rosnących indeksów). Kolejka ![A[a]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/7x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) w fazie
w fazie 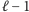 była wykorzystywana podczas obliczeń dla komórki
była wykorzystywana podczas obliczeń dla komórki ![|d[a,b −1],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/9x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) zatem zawiera pary
zatem zawiera pary ![|(i,t[i]+ d[a,i −1])](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/10x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) dla indeksów
dla indeksów ![s[a,b −1] < i ⩽ b − 1.](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/11x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) Ponieważ
Ponieważ ![|s[a, b− 1]⩽ s[a,b],](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/12x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) więc wystarczy usunąć z niej pary o indeksach nie większych niż
więc wystarczy usunąć z niej pary o indeksach nie większych niż ![s[a,b]](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/13x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) oraz dodać parę o indeksie
oraz dodać parę o indeksie 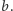 Analogicznie uaktualniamy pary w kolejce
Analogicznie uaktualniamy pary w kolejce ![B[b].](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/15x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-im-33,33,33-FF,FF,FF.gif) Pseudokod całego algorytmu jest następujący (zakładamy, że dla pustej kolejki pętla while nie wykonuje się, a operacja min zwraca
Pseudokod całego algorytmu jest następujący (zakładamy, że dla pustej kolejki pętla while nie wykonuje się, a operacja min zwraca 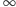 ):
):
![for ℓ = 0to n −1 do fora = 1ton − ℓdo b = a + ℓ; fori = s[a,b −1] to s[a+ 1,b] do ifd[a, i− 1]⩽ d[i + 1,b]then s[a, b] = i; A[a].push(b, t[b]+ d[a, b− 1]); whileA[a]. first ⩽ s[a, b]do A[a].pop; B[b].push(a, t[a]+ d[a + 1,b]); while B[b]. first > s[a,b]do B[b].pop; d[a,b] = min(A[a]. min,B[b]. min);](/math/temat/informatyka/algorytmy/2015/05/24/Wiercenia/17x-c2b617ee80dbd6dc913d0288fe6361c7067121b8-dm-33,33,33-FF,FF,FF.gif)
Kolejki możemy zaimplementować tak, aby wszystkie udostępniane operacje działały w zamortyzowanym czasie stałym. Zauważmy, że tuż przed wykonaniem operacji 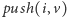 możemy usunąć z końca kolejki wszystkie pary o wartościach nie mniejszych niż
możemy usunąć z końca kolejki wszystkie pary o wartościach nie mniejszych niż 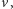 gdyż para
gdyż para 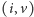 będzie lepszym kandydatem na minimum. Dzięki temu pary znajdujące się w kolejce będą zawsze posortowane rosnąco według wartości, zatem operacja
będzie lepszym kandydatem na minimum. Dzięki temu pary znajdujące się w kolejce będą zawsze posortowane rosnąco według wartości, zatem operacja 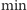 po prostu zwróci wartość pary z początku kolejki. Ostatecznie złożoność czasowa algorytmu wyniesie
po prostu zwróci wartość pary z początku kolejki. Ostatecznie złożoność czasowa algorytmu wyniesie