Informatyczny kącik olimpijski
Podział grafu
Jednym z najtrudniejszych zadań, z którym mierzyli się uczestnicy światowych finałów konkursu ACM ICPC w roku 2014, było zadanie pt. Metal Processing Plant.
Zadanie. Dany jest  -wierzchołkowy
-wierzchołkowy 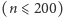 nieskierowany graf pełny. Dla każdej krawędzi
nieskierowany graf pełny. Dla każdej krawędzi 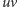 grafu znamy jej wagę
grafu znamy jej wagę 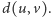 Wagą podzbioru wierzchołków
Wagą podzbioru wierzchołków 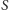 nazwiemy maksymalną wagę krawędzi po wszystkich parach wierzchołków z tego podzbioru, tzn.
nazwiemy maksymalną wagę krawędzi po wszystkich parach wierzchołków z tego podzbioru, tzn.

Należy znaleźć podział wierzchołków grafu na dwa podzbiory 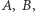 których sumaryczna waga
których sumaryczna waga 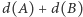 jest jak najmniejsza.
jest jak najmniejsza.
Załóżmy na początek, że zdecydowaliśmy, iż podzielimy graf na dwa podzbiory o wagach nie większych niż ustalone liczby 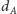 i
i 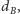 i chcemy stwierdzić, czy da się to zrobić. Innymi słowy, chcemy znaleźć dwa podzbiory
i chcemy stwierdzić, czy da się to zrobić. Innymi słowy, chcemy znaleźć dwa podzbiory 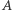 i
i 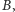 że
że 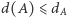 i
i 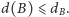 Dla każdego wierzchołka
Dla każdego wierzchołka  wprowadźmy zmienną logiczną
wprowadźmy zmienną logiczną 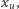 która oznaczać będzie, czy wierzchołek
która oznaczać będzie, czy wierzchołek 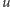 należy do podzbioru
należy do podzbioru 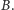 Skonstruujemy teraz listę zdań logicznych, które zakodują ograniczenia na wartości zmiennych.
Skonstruujemy teraz listę zdań logicznych, które zakodują ograniczenia na wartości zmiennych.
Każda z krawędzi 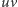 łączy dwa wierzchołki z podzbioru
łączy dwa wierzchołki z podzbioru 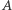 (wtedy
(wtedy 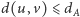 ), dwa wierzchołki z podzbioru
), dwa wierzchołki z podzbioru 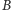 (wtedy
(wtedy 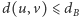 ) lub wierzchołki należące do różnych podzbiorów (i wtedy nie mamy ograniczenia na wagę tej krawędzi). Załóżmy bez straty ogólności, że
) lub wierzchołki należące do różnych podzbiorów (i wtedy nie mamy ograniczenia na wagę tej krawędzi). Załóżmy bez straty ogólności, że 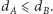
- (1)
- Jeśli
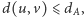 to wierzchołki
to wierzchołki 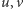 mogą znajdować się gdziekolwiek.
mogą znajdować się gdziekolwiek. - (2)
- Jeśli
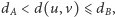 to co najmniej jeden z wierzchołków
to co najmniej jeden z wierzchołków 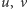 musi znajdować się w podzbiorze
musi znajdować się w podzbiorze 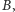 czyli musi być spełniona alternatywa
czyli musi być spełniona alternatywa 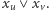
- (3)
- Jeśli
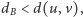 to wierzchołki
to wierzchołki 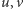 muszą znajdować się w różnych podzbiorach, czyli muszą być spełnione obie alternatywy
muszą znajdować się w różnych podzbiorach, czyli muszą być spełnione obie alternatywy 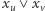 oraz
oraz 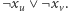
Każda z alternatyw zawiera dwie zmienne (lub ich negacje), zatem do znalezienia takich wartości zmiennych, które spełniają wszystkie alternatywy, możemy użyć algorytmu 2-SAT. Algorytm ten działa w czasie liniowym od liczby zmiennych i alternatyw, w naszym przypadku będzie to zatem czas 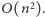
Jesteśmy już gotowi zaproponować pierwsze rozwiązanie naszego zadania. Ponieważ waga podzbioru jest równa wadze jednej z krawędzi grafu, więc mamy 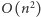 możliwości wyboru każdej z liczb
możliwości wyboru każdej z liczb 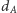 i
i 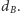 Sprawdzenie dla wszystkich tych wyborów, czy istnieje podział, i wybranie podziału dla najmniejszej sumy
Sprawdzenie dla wszystkich tych wyborów, czy istnieje podział, i wybranie podziału dla najmniejszej sumy 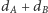 daje rozwiązanie działające w czasie
daje rozwiązanie działające w czasie 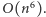 Jednak wybory te nie są zupełnie niezależne. Zauważmy, że jeśli dla pewnej pary
Jednak wybory te nie są zupełnie niezależne. Zauważmy, że jeśli dla pewnej pary 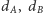 podział istnieje, to istnieje też dla pary o większych wartościach. Zatem dla ustalonej wartości
podział istnieje, to istnieje też dla pary o większych wartościach. Zatem dla ustalonej wartości 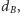 którą wybierzemy na
którą wybierzemy na 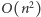 sposobów, możemy znaleźć najmniejszą wartość
sposobów, możemy znaleźć najmniejszą wartość 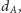 używając wyszukiwania binarnego w czasie
używając wyszukiwania binarnego w czasie 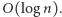 To da nam rozwiązanie działające w czasie
To da nam rozwiązanie działające w czasie 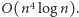
Okazuje się, że możemy istotnie zmniejszyć liczbę kandydatów na wartość 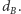 Powiemy, że krawędź
Powiemy, że krawędź 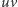 jest wewnętrzna, jeśli oba wierzchołki
jest wewnętrzna, jeśli oba wierzchołki 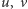 znajdują się w tym samym podzbiorze. Załóżmy, że znaleźliśmy maksymalne drzewo rozpinające grafu. Każda krawędź
znajdują się w tym samym podzbiorze. Załóżmy, że znaleźliśmy maksymalne drzewo rozpinające grafu. Każda krawędź 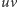 nienależąca do tego drzewa wyznacza cykl (w którym pozostałe krawędzie należą do drzewa). Jeśli cykl ten ma nieparzystą długość, to co najmniej jedna z jego krawędzi musi być wewnętrzna. Z kolei jeśli cykl ten ma parzystą długość i zawiera jakąś krawędź wewnętrzną, to musi zawierać co najmniej dwie takie krawędzie (a więc co najmniej jedną krawędź drzewową).
nienależąca do tego drzewa wyznacza cykl (w którym pozostałe krawędzie należą do drzewa). Jeśli cykl ten ma nieparzystą długość, to co najmniej jedna z jego krawędzi musi być wewnętrzna. Z kolei jeśli cykl ten ma parzystą długość i zawiera jakąś krawędź wewnętrzną, to musi zawierać co najmniej dwie takie krawędzie (a więc co najmniej jedną krawędź drzewową).
Załóżmy, że 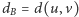 nie jest równe wadze żadnej krawędzi z maksymalnego drzewa rozpinającego, w szczególności krawędź wewnętrzna
nie jest równe wadze żadnej krawędzi z maksymalnego drzewa rozpinającego, w szczególności krawędź wewnętrzna 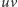 nie należy do drzewa. Jeśli ta krawędź wyznacza cykl długości parzystej, to na tym cyklu znajduje się jeszcze jedna krawędź wewnętrzna
nie należy do drzewa. Jeśli ta krawędź wyznacza cykl długości parzystej, to na tym cyklu znajduje się jeszcze jedna krawędź wewnętrzna 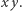 Ale wtedy
Ale wtedy 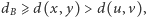 co daje sprzeczność. Zatem krawędź
co daje sprzeczność. Zatem krawędź  wyznacza cykl długości nieparzystej. Rozważmy krawędź niedrzewową
wyznacza cykl długości nieparzystej. Rozważmy krawędź niedrzewową 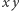 wyznaczającą nieparzysty cykl, taką że waga
wyznaczającą nieparzysty cykl, taką że waga 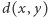 jest maksymalna; zatem
jest maksymalna; zatem 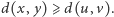 Ponieważ
Ponieważ 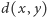 jest minimalną wagą na tym cyklu i cykl ten zawiera krawędź wewnętrzną, to
jest minimalną wagą na tym cyklu i cykl ten zawiera krawędź wewnętrzną, to 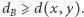 Tak więc w tym przypadku
Tak więc w tym przypadku 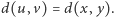
Z tego wynika, że mamy 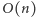 kandydatów na wartość
kandydatów na wartość 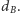 Są to wagi wszystkich krawędzi należących do drzewa oraz maksimum z wag krawędzi niedrzewowych tworzących cykle o nieparzystej długości. Drzewo rozpinające można znaleźć algorytmem Kruskala w czasie
Są to wagi wszystkich krawędzi należących do drzewa oraz maksimum z wag krawędzi niedrzewowych tworzących cykle o nieparzystej długości. Drzewo rozpinające można znaleźć algorytmem Kruskala w czasie 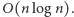 Jeśli wykonamy dwukolorowanie tego drzewa w czasie
Jeśli wykonamy dwukolorowanie tego drzewa w czasie 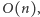 to będziemy mogli dla każdej niedrzewowej krawędzi odpowiadać w czasie stałym, czy tworzy ona cykl nieparzystej długości.
to będziemy mogli dla każdej niedrzewowej krawędzi odpowiadać w czasie stałym, czy tworzy ona cykl nieparzystej długości.
Ostatecznie dostajemy algorytm działający w czasie