Informatyczny kącik olimpijski
Fotoradary
W tym kąciku omówimy zadanie Fotoradary, które pojawiło się w 2013 roku na Akademickich Mistrzostwach Polski w Programowaniu Zespołowym.
Zadanie. W Bajtogrodzie jest 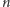 skrzyżowań, połączonych
skrzyżowań, połączonych 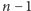 dwukierunkowymi odcinkami dróg, które umożliwiają dotarcie z każdego skrzyżowania do wszystkich pozostałych. Burmistrz Bajtogrodu zamierza postawić na skrzyżowaniach jak najwięcej fotoradarów (na każdym co najwyżej jeden). Aby nie denerwować zbytnio bajtogrodzkich kierowców, przyjął on, że na każdej trasie może stać co najwyżej
dwukierunkowymi odcinkami dróg, które umożliwiają dotarcie z każdego skrzyżowania do wszystkich pozostałych. Burmistrz Bajtogrodu zamierza postawić na skrzyżowaniach jak najwięcej fotoradarów (na każdym co najwyżej jeden). Aby nie denerwować zbytnio bajtogrodzkich kierowców, przyjął on, że na każdej trasie może stać co najwyżej 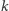 fotoradarów.
fotoradarów.
Innymi słowy, w zadaniu mamy dane drzewo o 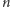 wierzchołkach i mamy zaznaczyć w nim jak najwięcej wierzchołków tak, by na każdej ścieżce prostej było zaznaczonych co najwyżej
wierzchołkach i mamy zaznaczyć w nim jak najwięcej wierzchołków tak, by na każdej ścieżce prostej było zaznaczonych co najwyżej 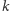 wierzchołków.
wierzchołków.
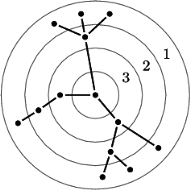
Rys. 1 Podział wierzchołków drzewa na warstwy.
Zadanie ma całkiem proste rozwiązanie zachłanne. Podzielmy wierzchołki na warstwy (Rys. 1). W 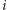 -tej warstwie (licząc od 1) będą znajdować się wierzchołki, które zostają liśćmi po usunięciu warstw o numerach
-tej warstwie (licząc od 1) będą znajdować się wierzchołki, które zostają liśćmi po usunięciu warstw o numerach 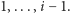 Jeśli
Jeśli 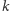 jest parzyste, to zaznaczamy wierzchołki na pierwszych
jest parzyste, to zaznaczamy wierzchołki na pierwszych 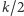 warstwach (oczywiście, jeśli jest mniej niż
warstwach (oczywiście, jeśli jest mniej niż 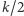 warstw, to bierzemy wszystko). Jeśli
warstw, to bierzemy wszystko). Jeśli 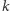 jest nieparzyste, to zaznaczamy
jest nieparzyste, to zaznaczamy 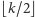 warstw oraz dowolny inny wierzchołek (jeśli jakiś pozostał).
warstw oraz dowolny inny wierzchołek (jeśli jakiś pozostał).
Powyższy pomysł można zrealizować w czasie 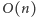 : utrzymujemy kolejkę wierzchołków o stopniu 1 i usuwamy kolejne warstwy, uaktualniając stopnie wierzchołków.
: utrzymujemy kolejkę wierzchołków o stopniu 1 i usuwamy kolejne warstwy, uaktualniając stopnie wierzchołków.
Alternatywne rozwiązanie wyznacza numery warstw dla wierzchołków, korzystając z metody programowania dynamicznego. Numer warstwy dla wierzchołka  jest to druga co do wielkości wysokość poddrzewa zaczepionego w dziecku
jest to druga co do wielkości wysokość poddrzewa zaczepionego w dziecku  plus 1.
plus 1.
Pozostaje nam pokazać poprawność algorytmu zachłannego. Zauważmy, że wystarczy badać, czy warunek poprawności (nie więcej niż 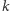 zaznaczonych wierzchołków na ścieżce) jest spełniony na każdej ścieżce prostej od liścia do liścia. Oczywiste jest, że nasz algorytm znajduje poprawny podzbiór wierzchołków, i należy wykazać, że jest on optymalny (najliczniejszy). Ponadto widać, że dołożenie dowolnego wierzchołka do znalezionego podzbioru powoduje, że podzbiór staje się niepoprawny.
zaznaczonych wierzchołków na ścieżce) jest spełniony na każdej ścieżce prostej od liścia do liścia. Oczywiste jest, że nasz algorytm znajduje poprawny podzbiór wierzchołków, i należy wykazać, że jest on optymalny (najliczniejszy). Ponadto widać, że dołożenie dowolnego wierzchołka do znalezionego podzbioru powoduje, że podzbiór staje się niepoprawny.
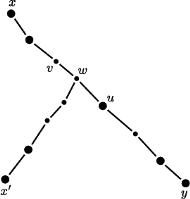
Rys. 2 Ilustracja dowodu poprawności; zaznaczone wierzchołki są pogrubione.
Ustalmy 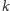 parzyste i oznaczmy przez
parzyste i oznaczmy przez 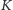 zbiór wierzchołków z pierwszych
zbiór wierzchołków z pierwszych 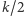 warstw. Weźmy dowolne rozwiązanie optymalne i załóżmy, że pewien wierzchołek
warstw. Weźmy dowolne rozwiązanie optymalne i załóżmy, że pewien wierzchołek 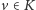 nie został w tym rozwiązaniu zaznaczony (Rys. 2). Jeśli jest więcej takich wierzchołków, to weźmy ten z warstwy o najmniejszym numerze (i oznaczmy numer tej warstwy przez
nie został w tym rozwiązaniu zaznaczony (Rys. 2). Jeśli jest więcej takich wierzchołków, to weźmy ten z warstwy o najmniejszym numerze (i oznaczmy numer tej warstwy przez 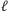 ). Rozważmy pewien zaznaczony wierzchołek
). Rozważmy pewien zaznaczony wierzchołek 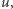 który jest na warstwie wyższej niż
który jest na warstwie wyższej niż 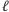 i taki, że pomiędzy
i taki, że pomiędzy  i
i  nie ma zaznaczonych wierzchołków (gdyby wierzchołek
nie ma zaznaczonych wierzchołków (gdyby wierzchołek  nie istniał, to by znaczyło, że rozwiązanie ma za mało zaznaczonych wierzchołków, aby być optymalne). Pokażemy teraz, że usuwając ze zbioru zaznaczonych wierzchołków
nie istniał, to by znaczyło, że rozwiązanie ma za mało zaznaczonych wierzchołków, aby być optymalne). Pokażemy teraz, że usuwając ze zbioru zaznaczonych wierzchołków 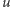 i dodając
i dodając 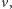 dostaniemy poprawne rozwiązanie.
dostaniemy poprawne rozwiązanie.
Rozważmy zatem dowolną ścieżkę 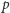 od liścia
od liścia  do liścia
do liścia 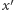 i pokażmy, że po zamianie zawiera ona nadal nie więcej niż
i pokażmy, że po zamianie zawiera ona nadal nie więcej niż 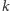 zaznaczonych wierzchołków. Podejrzana ścieżka
zaznaczonych wierzchołków. Podejrzana ścieżka 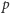 musi zawierać wierzchołek
musi zawierać wierzchołek 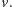 Jeśli zawiera również wierzchołek
Jeśli zawiera również wierzchołek 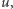 to po zamianie liczba zaznaczonych wierzchołków w
to po zamianie liczba zaznaczonych wierzchołków w 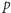 nie zmieni się. Załóżmy zatem, że
nie zmieni się. Załóżmy zatem, że 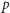 nie zawiera
nie zawiera  i rozważmy dowolną ścieżkę od liścia
i rozważmy dowolną ścieżkę od liścia  do liścia
do liścia 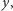 która zawiera oba wierzchołki
która zawiera oba wierzchołki  i
i 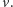 Niech
Niech 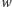 będzie wierzchołkiem pomiędzy
będzie wierzchołkiem pomiędzy  a
a  który rozdziela te ścieżki. Ścieżka z
który rozdziela te ścieżki. Ścieżka z 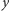 do
do 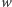 zawierała przed zamianą co najmniej
zawierała przed zamianą co najmniej 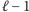 zaznaczonych wierzchołków na jej końcu (bo założyliśmy, że najmniejsza warstwa z niezaznaczonym wierzchołkiem to
zaznaczonych wierzchołków na jej końcu (bo założyliśmy, że najmniejsza warstwa z niezaznaczonym wierzchołkiem to 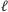 ) plus dodatkowo wierzchołek
) plus dodatkowo wierzchołek  Z kolei ścieżka z
Z kolei ścieżka z  do
do 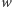 po zamianie zawiera dokładnie
po zamianie zawiera dokładnie 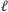 wierzchołków (pamiętamy, że pomiędzy
wierzchołków (pamiętamy, że pomiędzy  a
a 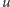 nie ma zaznaczonych wierzchołków). Zatem poprawna przed zamianą ścieżka z
nie ma zaznaczonych wierzchołków). Zatem poprawna przed zamianą ścieżka z 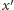 do
do 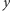 zawierała co najmniej tyle zaznaczonych wierzchołków, co ścieżka
zawierała co najmniej tyle zaznaczonych wierzchołków, co ścieżka 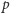 po zamianie. To dowodzi poprawności ścieżki
po zamianie. To dowodzi poprawności ścieżki 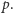
Tak więc, korzystając wielokrotnie z udowodnionego faktu, stwierdzamy, że istnieje rozwiązanie optymalne, które zaznacza wszystkie wierzchołki z 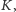 zatem zbiór wierzchołków generowany przez nasz algorytm jest najliczniejszy. Dowód dla
zatem zbiór wierzchołków generowany przez nasz algorytm jest najliczniejszy. Dowód dla 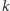 nieparzystego zostawiamy jako ćwiczenie dla Czytelnika.
nieparzystego zostawiamy jako ćwiczenie dla Czytelnika.