Informatyczny kącik olimpijski
Wybrakowany ciąg
W tym miesiącu omówimy zadanie Sequence, które pojawiło się na tegorocznej edycji Bałtyckiej Olimpiady Informatycznej.
Zadanie. Na tablicy napisano 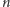 kolejnych liczb całkowitych
kolejnych liczb całkowitych 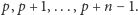 Następnie z każdej liczby usunięto wszystkie cyfry oprócz jednej. Znając ciąg
Następnie z każdej liczby usunięto wszystkie cyfry oprócz jednej. Znając ciąg 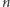 cyfr
cyfr 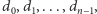 które pozostały na tablicy, należy wyznaczyć minimalną wartość
które pozostały na tablicy, należy wyznaczyć minimalną wartość 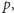 od której mógł zaczynać się pierwotny ciąg.
od której mógł zaczynać się pierwotny ciąg.
Przykładowo, ciąg cyfr 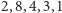 mógł powstać z pięciu kolejnych liczb naturalnych w następujący sposób:
mógł powstać z pięciu kolejnych liczb naturalnych w następujący sposób: 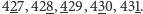
Zacznijmy od prostej obserwacji, że dla każdego ciągu cyfr szukana liczba 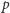 istnieje. Wystarczy zauważyć, że dla
istnieje. Wystarczy zauważyć, że dla 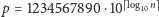 wszystkie liczby z ciągu
wszystkie liczby z ciągu 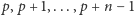 zaczynają się od prefiksu zawierającego wszystkie możliwe cyfry.
zaczynają się od prefiksu zawierającego wszystkie możliwe cyfry.
Zadanie jest niełatwe i tylko jeden z uczestników olimpiady zdobył za nie maksymalną liczbę punktów. Kluczowe dla rozwiązania jest przyjrzenie się cyfrze jedności liczby 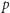 ; oznaczmy ją przez
; oznaczmy ją przez 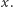 Wyznacza ona jednoznacznie cyfry jedności pozostałych liczb pierwotnego ciągu - będą to kolejno
Wyznacza ona jednoznacznie cyfry jedności pozostałych liczb pierwotnego ciągu - będą to kolejno

Jeśli 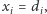 to pozostałe cyfry
to pozostałe cyfry 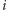 -tej liczby mogą być dowolne. W przeciwnym przypadku cyfra
-tej liczby mogą być dowolne. W przeciwnym przypadku cyfra 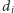 musi się pojawić na dalszej pozycji w
musi się pojawić na dalszej pozycji w 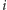 -tej liczbie. Podzielmy teraz poszukiwany ciąg na bloki zaczynające się na takich pozycjach, że
-tej liczbie. Podzielmy teraz poszukiwany ciąg na bloki zaczynające się na takich pozycjach, że 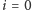 lub
lub 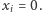 Każdy blok (oprócz pierwszego i ostatniego, które mogą być krótsze) zawiera 10 liczb, które w pierwotnym ciągu będą się różnić jedynie na cyfrze jedności. Zatem ich wspólny prefiks będzie musiał zawierać wszystkie cyfry ze zbioru
Każdy blok (oprócz pierwszego i ostatniego, które mogą być krótsze) zawiera 10 liczb, które w pierwotnym ciągu będą się różnić jedynie na cyfrze jedności. Zatem ich wspólny prefiks będzie musiał zawierać wszystkie cyfry ze zbioru 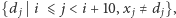 gdzie
gdzie 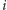 jest początkową pozycją bloku. Możemy więc rozważyć 10 razy krótszy ciąg - jego elementy będą zbiorami cyfr, które muszą wystąpić w kolejnych blokach, i powtórzyć powyższe rozumowanie.
jest początkową pozycją bloku. Możemy więc rozważyć 10 razy krótszy ciąg - jego elementy będą zbiorami cyfr, które muszą wystąpić w kolejnych blokach, i powtórzyć powyższe rozumowanie.
Zatem zadanie rozwiązujemy rekurencyjnie: dla danego 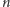 -elementowego ciągu
-elementowego ciągu 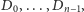 zawierającego zbiory cyfr, które mają wystąpić w kolejnych liczbach, należy wyznaczyć minimalne
zawierającego zbiory cyfr, które mają wystąpić w kolejnych liczbach, należy wyznaczyć minimalne 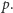 Jeśli
Jeśli 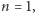 to odpowiedzią jest liczba zawierająca wszystkie cyfry ze zbioru
to odpowiedzią jest liczba zawierająca wszystkie cyfry ze zbioru 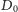 (w kolejności rosnącej). Dla
(w kolejności rosnącej). Dla 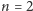 mamy dwa przypadki: albo
mamy dwa przypadki: albo 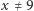 i wtedy liczby mają ten sam prefiks, więc rekurencyjnie znajdujemy rozwiązanie dla zbioru cyfr
i wtedy liczby mają ten sam prefiks, więc rekurencyjnie znajdujemy rozwiązanie dla zbioru cyfr 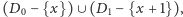 albo
albo 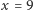 i rekurencyjnie rozpatrujemy ciąg
i rekurencyjnie rozpatrujemy ciąg 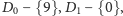 wiedząc, że nie opłaca nam się więcej rozpatrywać drugiego przypadku. Zatem rozwiązanie dla ciągów długości
wiedząc, że nie opłaca nam się więcej rozpatrywać drugiego przypadku. Zatem rozwiązanie dla ciągów długości 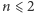 znajdujemy w czasie stałym.
znajdujemy w czasie stałym.
W końcu dla 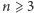 przeglądamy wszystkich 10 kandydatów
przeglądamy wszystkich 10 kandydatów 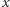 na cyfrę jedności
na cyfrę jedności 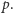 Dla każdego z nich budujemy ciąg o długości
Dla każdego z nich budujemy ciąg o długości 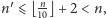 zawierający sumy zbiorów dla kolejnych bloków, i rekurencyjnie wyznaczamy dla niego wartość
zawierający sumy zbiorów dla kolejnych bloków, i rekurencyjnie wyznaczamy dla niego wartość 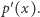 Szukane
Szukane 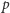 to minimum ze zbioru
to minimum ze zbioru 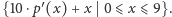
Złożoność czasowa algorytmu wyraża się wzorem rekurencyjnym

którego rozwiązaniem jest 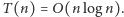
Niestety, powyższy algorytm ma dość istotny feler - działa przy założeniu, że liczby w pierwotnym ciągu mogą mieć zera wiodące (np. dla 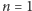 i zbioru
i zbioru 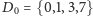 konstruujemy
konstruujemy 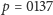 zamiast poprawnego
zamiast poprawnego 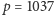 ). I, jak to zwykle bywa w zadaniach tego typu, naprawienie tej usterki wymaga dość żmudnego przyjrzenia się poszczególnym przypadkom, w którym takie zero może się pojawić. W szczególności, gdy cyfra jedności jednej z liczb należącej do bloku jest "istotnym" zerem (czyli
). I, jak to zwykle bywa w zadaniach tego typu, naprawienie tej usterki wymaga dość żmudnego przyjrzenia się poszczególnym przypadkom, w którym takie zero może się pojawić. W szczególności, gdy cyfra jedności jednej z liczb należącej do bloku jest "istotnym" zerem (czyli 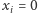 oraz
oraz 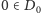 ), wygodnie jest dorzucić do zbioru
), wygodnie jest dorzucić do zbioru 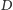 odpowiadającego temu blokowi dodatkowy element sygnalizujący, że w
odpowiadającego temu blokowi dodatkowy element sygnalizujący, że w 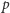 musi wystąpić jakaś niezerowa cyfra. Szczegóły techniczne pozostawimy do dopracowania Czytelnikom.
musi wystąpić jakaś niezerowa cyfra. Szczegóły techniczne pozostawimy do dopracowania Czytelnikom.