Informatyczny kącik olimpijski
Skarb
Zadanie Skarb pojawiło się w kwalifikacjach do konkursu Google Code Jam 2013.
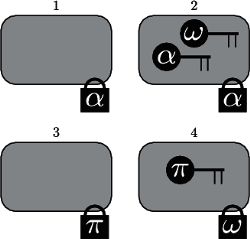
Mamy cztery szkatułki i trzy zamknięte klucze. Rodzaje kluczy i kłódek oznaczone są literami greckimi. Początkowo mamy jeden klucz rodzaju 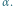 Jedna z kolejności otwarcia wszystkich szkatułek to 2, 1, 4, 3. Jeśli zaczniemy od otwarcia szkatułki 1, to nie będziemy w stanie otworzyć już żadnej innej.
Jedna z kolejności otwarcia wszystkich szkatułek to 2, 1, 4, 3. Jeśli zaczniemy od otwarcia szkatułki 1, to nie będziemy w stanie otworzyć już żadnej innej.
Zadanie. W skarbcu znajduje się 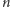 szkatułek, każda z nich zamknięta na kłódkę, która może być otwarta kluczem określonego rodzaju. W szkatułkach, oprócz kosztowności, mogą znajdować się klucze, które można wykorzystać do otwarcia innych szkatułek (w sumie jest
szkatułek, każda z nich zamknięta na kłódkę, która może być otwarta kluczem określonego rodzaju. W szkatułkach, oprócz kosztowności, mogą znajdować się klucze, które można wykorzystać do otwarcia innych szkatułek (w sumie jest 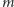 kluczy). Klucz, którym otworzyliśmy szkatułkę, nie może być użyty ponownie. Wchodząc do skarbca, mamy już kilka kluczy. Znając zawartość szkatułek, należy stwierdzić, czy istnieje taka kolejność ich otwierania, która pozwoli na otwarcie ich wszystkich (patrz rysunek).
kluczy). Klucz, którym otworzyliśmy szkatułkę, nie może być użyty ponownie. Wchodząc do skarbca, mamy już kilka kluczy. Znając zawartość szkatułek, należy stwierdzić, czy istnieje taka kolejność ich otwierania, która pozwoli na otwarcie ich wszystkich (patrz rysunek).
Zadanie jest całkiem trudne, spróbujmy więc rozwiązać jego prostszy wariant, w którym zaczynamy z jednym kluczem rodzaju 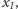 a w każdej szkatułce jest co najwyżej jeden klucz. Zauważmy, że następujący warunek jest konieczny, by rozwiązanie istniało:
a w każdej szkatułce jest co najwyżej jeden klucz. Zauważmy, że następujący warunek jest konieczny, by rozwiązanie istniało:
- (A) kluczy ustalonego rodzaju musi być co najmniej tyle, ile jest kłódek tego rodzaju.
W szczególności oznacza to, że co najwyżej jedna szkatułka może być pusta. Otwarcie szkatułki zamkniętej na kłódkę rodzaju 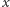 i zawierającej klucz rodzaju
i zawierającej klucz rodzaju 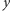 skutkuje wymienieniem klucza
skutkuje wymienieniem klucza 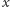 na klucz
na klucz 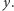 Sytuację możemy więc przedstawić za pomocą skierowanego multigrafu
Sytuację możemy więc przedstawić za pomocą skierowanego multigrafu 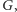 którego wierzchołkami będą rodzaje kluczy, a skierowana krawędź
którego wierzchołkami będą rodzaje kluczy, a skierowana krawędź 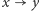 będzie istnieć dla każdej szkatułki zamkniętej na kłódkę rodzaju
będzie istnieć dla każdej szkatułki zamkniętej na kłódkę rodzaju 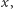 która zawiera w sobie klucz rodzaju
która zawiera w sobie klucz rodzaju 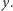 Każda ścieżka w
Każda ścieżka w 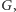 startująca z wierzchołka
startująca z wierzchołka 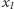 opisuje możliwą do zrealizowania procedurę otwierania szkatułek (otwieramy szkatułki odpowiadające kolejnym krawędziom ścieżki). Innymi słowy, rozwiązanie istnieje, jeśli w multigrafie
opisuje możliwą do zrealizowania procedurę otwierania szkatułek (otwieramy szkatułki odpowiadające kolejnym krawędziom ścieżki). Innymi słowy, rozwiązanie istnieje, jeśli w multigrafie 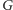 istnieje ścieżka Eulera z wierzchołka
istnieje ścieżka Eulera z wierzchołka 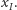 Czytelnicy na pewno znają warunki, jakie musi spełniać skierowany multigraf, aby taka ścieżka istniała: (a) każdy wierzchołek musi mieć stopień wyjściowy równy wejściowemu (oprócz co najwyżej dwóch, w których te liczby mogą się różnić o 1) oraz (b) graf musi być (słabo) spójny.
Czytelnicy na pewno znają warunki, jakie musi spełniać skierowany multigraf, aby taka ścieżka istniała: (a) każdy wierzchołek musi mieć stopień wyjściowy równy wejściowemu (oprócz co najwyżej dwóch, w których te liczby mogą się różnić o 1) oraz (b) graf musi być (słabo) spójny.
Nietrudno się przekonać, że warunek (a) wynika z warunku (A) i tego, że w każdej szkatułce jest co najwyżej jeden klucz. Jeśli założymy, że warunek (a) jest spełniony, to warunek (b) jest równoważny temu, że
- (B)
- dla każdego rodzaju klucza da się zdobyć co najmniej jeden klucz tego rodzaju.
Nieprzypadkowo wyróżniliśmy warunki (A) i (B). Okazuje się bowiem, że są one konieczne i wystarczające do tego, by istniało rozwiązanie zadania w pełnej ogólności. (Tym razem w 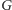 mamy krawędź
mamy krawędź 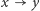 dla każdego klucza rodzaju
dla każdego klucza rodzaju 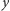 zamkniętego w szkatułce na kłódkę rodzaju
zamkniętego w szkatułce na kłódkę rodzaju 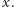 ) Konieczność jest oczywista. Ponadto jeśli początkowa konfiguracja szkatułek spełnia warunek (A), to otwieranie szkatułek tego warunku nie popsuje (otwarcie szkatułki "zużywa" nam jeden klucz i kłódkę tego samego rodzaju). Pozostaje zatem udowodnić, że dla każdej konfiguracji spełniającej oba warunki istnieje szkatułka, której otworzenie doprowadzi do konfiguracji spełniającej warunek (B).
) Konieczność jest oczywista. Ponadto jeśli początkowa konfiguracja szkatułek spełnia warunek (A), to otwieranie szkatułek tego warunku nie popsuje (otwarcie szkatułki "zużywa" nam jeden klucz i kłódkę tego samego rodzaju). Pozostaje zatem udowodnić, że dla każdej konfiguracji spełniającej oba warunki istnieje szkatułka, której otworzenie doprowadzi do konfiguracji spełniającej warunek (B).

Załóżmy, że mamy klucz dowolnego rodzaju 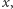 który otwiera pewną szkatułkę. Jeśli mamy wszystkie klucze tego rodzaju, to z warunku (A) możemy otworzyć wszystkie szkatułki zamknięte na kłódki rodzaju
który otwiera pewną szkatułkę. Jeśli mamy wszystkie klucze tego rodzaju, to z warunku (A) możemy otworzyć wszystkie szkatułki zamknięte na kłódki rodzaju 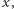 i warunek (B) będzie nadal spełniony.
i warunek (B) będzie nadal spełniony.
W przeciwnym przypadku istnieje szkatułka zawierająca klucz rodzaju 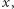 a z warunku (B) wynika, że istnieje ciąg rodzajów kluczy
a z warunku (B) wynika, że istnieje ciąg rodzajów kluczy 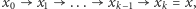 który pozwala na zdobycie klucza
który pozwala na zdobycie klucza 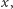 zakładając posiadanie przez nas klucza
zakładając posiadanie przez nas klucza 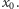 Załóżmy, że jest to najkrótszy taki ciąg, zatem
Załóżmy, że jest to najkrótszy taki ciąg, zatem 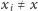 dla
dla 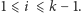
Jeśli 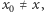 to możemy użyć klucza rodzaju
to możemy użyć klucza rodzaju  do otwarcia dowolnej szkatułki. Aby pokazać, że nie popsuje to warunku (B), rozważmy klucz dowolnego rodzaju
do otwarcia dowolnej szkatułki. Aby pokazać, że nie popsuje to warunku (B), rozważmy klucz dowolnego rodzaju 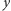 (być może
(być może 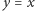 ) i ciąg rodzajów kluczy
) i ciąg rodzajów kluczy 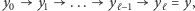 który pozwalał go zdobyć. Jedyna wątpliwość pojawia się, gdy
który pozwalał go zdobyć. Jedyna wątpliwość pojawia się, gdy  występuje w tym ciągu, zatem ciągi te mają jakiś element wspólny. Niech
występuje w tym ciągu, zatem ciągi te mają jakiś element wspólny. Niech 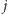 będzie największym takim indeksem, że
będzie największym takim indeksem, że 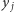 równa się pewnemu
równa się pewnemu 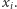 Wtedy, po użyciu klucza
Wtedy, po użyciu klucza  możemy nadal dostać się do klucza
możemy nadal dostać się do klucza 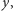 wykonując operacje z ciągu
wykonując operacje z ciągu 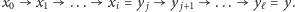
Z kolei jeśli 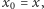 to otwieramy szkatułkę zawierającą klucz rodzaju
to otwieramy szkatułkę zawierającą klucz rodzaju 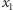 i, powtarzając powyższe rozumowanie, również dowodzimy, że warunek (B) jest nadal spełniony.
i, powtarzając powyższe rozumowanie, również dowodzimy, że warunek (B) jest nadal spełniony.
Ostatecznie udowodniliśmy, że dla każdej konfiguracji spełniającej warunki (A) i (B) istnieje szkatułka, którą możemy otworzyć, aby uzyskać nową konfigurację również spełniającą oba warunki. Wykonując tę operację 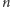 razy, otworzymy wszystkie szkatułki. Jeśli chodzi o implementację, to sprawdzenie warunku (A) jest trywialne, zaś warunek (B) sprowadza się do przeszukania multigrafu
razy, otworzymy wszystkie szkatułki. Jeśli chodzi o implementację, to sprawdzenie warunku (A) jest trywialne, zaś warunek (B) sprowadza się do przeszukania multigrafu 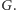 Można to zrobić w czasie
Można to zrobić w czasie 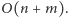
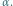 Jedna z kolejności otwarcia wszystkich szkatułek to 2, 1, 4, 3. Jeśli zaczniemy od otwarcia szkatułki 1, to nie będziemy w stanie otworzyć już żadnej innej.
Jedna z kolejności otwarcia wszystkich szkatułek to 2, 1, 4, 3. Jeśli zaczniemy od otwarcia szkatułki 1, to nie będziemy w stanie otworzyć już żadnej innej.