Informatyczny kącik olimpijski
Smok i owce
Tym razem zadanie Smok z Akademickich Mistrzostw Polski w Programowaniu Zespołowym 2005, które odbyły się na Uniwersytecie Jagiellońskim.

Jeśli mamy 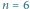 pastwisk jak powyżej (liczba owiec w prostokątach), to jeden z optymalnych planów smoka jest następujący: pożera on 9 owiec z trzeciego pastwiska (płosząc 5 owiec z pierwszych dwóch pastwisk), następnie zjada 6 owiec z piątego pastwiska i w końcu 1 owcę z czwartego pastwiska.
pastwisk jak powyżej (liczba owiec w prostokątach), to jeden z optymalnych planów smoka jest następujący: pożera on 9 owiec z trzeciego pastwiska (płosząc 5 owiec z pierwszych dwóch pastwisk), następnie zjada 6 owiec z piątego pastwiska i w końcu 1 owcę z czwartego pastwiska.
Zadanie. W długiej i głębokiej dolinie znajduje się  kolejno położonych pastwisk, na
kolejno położonych pastwisk, na 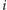 -tym z nich pasie się
-tym z nich pasie się 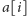 owiec. Każdego dnia dolinę może nawiedzić smok i pożreć owce z jednego pastwiska. Smok musi zawsze lecieć wzdłuż doliny (ale może wybrać, z której strony przyleci danego dnia), a z każdego pastwiska, nad którym przeleci, wszystkie owce uciekają. Ponadto pod koniec każdego dnia liczebność owiec (czy to z powodu wilków, czy pogłosek o smokach) na każdym pastwisku zmniejsza się o jeden. Należy obliczyć, ile maksymalnie owiec uda się pożreć smokowi (patrz rysunek).
owiec. Każdego dnia dolinę może nawiedzić smok i pożreć owce z jednego pastwiska. Smok musi zawsze lecieć wzdłuż doliny (ale może wybrać, z której strony przyleci danego dnia), a z każdego pastwiska, nad którym przeleci, wszystkie owce uciekają. Ponadto pod koniec każdego dnia liczebność owiec (czy to z powodu wilków, czy pogłosek o smokach) na każdym pastwisku zmniejsza się o jeden. Należy obliczyć, ile maksymalnie owiec uda się pożreć smokowi (patrz rysunek).
Zauważmy, że niezależnie od poczynań smoka pastwiska, które nie zostały przez niego odwiedzone (tzn. owce na tych pastwiskach nie zostały przez niego ani pożarte, ani spłoszone), leżą w spójnym fragmencie doliny. To sugeruje następujące rozwiązanie dynamiczne: wypełniamy tabelkę, w której 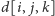 oznacza maksymalną liczbę pożartych owiec, jeśli pastwiska nieodwiedzone leżą w przedziale
oznacza maksymalną liczbę pożartych owiec, jeśli pastwiska nieodwiedzone leżą w przedziale 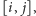 a smok wykonuje
a smok wykonuje 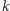 -ty lot. Pomijając przypadki brzegowe, następująca rekurencja pozwala wyznaczyć tabelkę w czasie
-ty lot. Pomijając przypadki brzegowe, następująca rekurencja pozwala wyznaczyć tabelkę w czasie 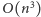 :
:
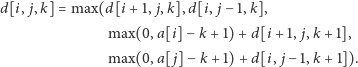 |
Widać, że problemy smoka są dwa: które pastwiska wybrać i w jakiej kolejności je odwiedzać. Załóżmy, że w pewnym optymalnym rozwiązaniu smok odwiedza kolejno pastwiska o numerach 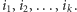 Ponieważ na każdym z nich się posili, zatem
Ponieważ na każdym z nich się posili, zatem 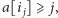 i w sumie zje
i w sumie zje 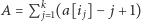 owiec. A czy istnieje inna kolejność, w której może on odwiedzać te pastwiska? Zauważmy, że liczba owiec z pastwiska
owiec. A czy istnieje inna kolejność, w której może on odwiedzać te pastwiska? Zauważmy, że liczba owiec z pastwiska 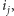 które nie zostaną pożarte przez smoka, wynosi
które nie zostaną pożarte przez smoka, wynosi  zatem w sumie nie pożre on
zatem w sumie nie pożre on 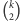 owiec. Ale jeśli smok nie będzie latał kompletnie bez sensu (tzn. nie będzie płoszył owiec na pastwiskach
owiec. Ale jeśli smok nie będzie latał kompletnie bez sensu (tzn. nie będzie płoszył owiec na pastwiskach 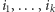 ), to po
), to po 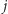 -tym przelocie liczba owiec zmniejszy się co najwyżej o
-tym przelocie liczba owiec zmniejszy się co najwyżej o  zatem w sumie zmniejszy się co najwyżej o
zatem w sumie zmniejszy się co najwyżej o 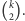 Zatem, odwiedzając pastwiska np. w kolejności od prawej do lewej, smok zje co najmniej
Zatem, odwiedzając pastwiska np. w kolejności od prawej do lewej, smok zje co najmniej 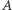 owiec, czyli tyle, ile w rozwiązaniu optymalnym.
owiec, czyli tyle, ile w rozwiązaniu optymalnym.
To pozwala nam uprościć i przyspieszyć nasze rozwiązanie dynamiczne do działającego w czasie 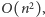 rozważając jedynie przedziały postaci
rozważając jedynie przedziały postaci 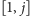 :
:

Spróbujmy podejść do problemu jeszcze inaczej. Załóżmy przez chwilę, że smok swoim lotem nie straszy owiec. Może wtedy odwiedzać pastwiska w dowolnej kolejności, zatem naturalne jest, że opłaca mu się zastosować strategię zachłanną i zaczynać od pastwisk, na których owiec jest jak najwięcej. Niech 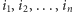 będzie ciągiem numerów pastwisk uporządkowanym nierosnąco względem liczby owiec, tzn.
będzie ciągiem numerów pastwisk uporządkowanym nierosnąco względem liczby owiec, tzn. 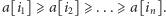 Zachłanny smok pożre
Zachłanny smok pożre

owiec i będzie ucztował na pastwiskach 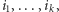 gdzie
gdzie 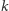 jest ostatnim indeksem, dla którego
jest ostatnim indeksem, dla którego 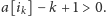 Ale, jak udowodniliśmy wcześniej, odwiedzając pastwiska ze zbioru
Ale, jak udowodniliśmy wcześniej, odwiedzając pastwiska ze zbioru 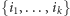 w kolejności od prawej do lewej, smok pożre co najmniej
w kolejności od prawej do lewej, smok pożre co najmniej 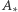 owiec i nie spłoszy żadnej owcy z tego zbioru. Zatem
owiec i nie spłoszy żadnej owcy z tego zbioru. Zatem 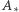 jest optymalną liczbą pożartych owiec, a do jej wyznaczenia wystarczy posortować dany na wejściu ciąg, co można zrobić w czasie
jest optymalną liczbą pożartych owiec, a do jej wyznaczenia wystarczy posortować dany na wejściu ciąg, co można zrobić w czasie 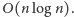
Okazuje się, że powyższe zadanie można uogólnić, a rozwiązanie nadal będzie działać. Jeśli przedstawimy dolinę jako graf nieskierowany, w którym wierzchołki oznaczać będą pastwiska, a krawędzie łączyć będą te z nich, pomiędzy którymi może przelecieć smok, to dostaniemy graf o jednej ścieżce. Możemy więc zamiast niego rozważyć dowolny graf nieskierowany. To było treścią zadania Godzilla z Obozu Naukowo-Treningowego im. A. Kreczmara w 2010 roku.
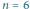 pastwisk jak powyżej (liczba owiec w prostokątach), to jeden z optymalnych planów smoka jest następujący: pożera on 9 owiec z trzeciego pastwiska (płosząc 5 owiec z pierwszych dwóch pastwisk), następnie zjada 6 owiec z piątego pastwiska i w końcu 1 owcę z czwartego pastwiska.
pastwisk jak powyżej (liczba owiec w prostokątach), to jeden z optymalnych planów smoka jest następujący: pożera on 9 owiec z trzeciego pastwiska (płosząc 5 owiec z pierwszych dwóch pastwisk), następnie zjada 6 owiec z piątego pastwiska i w końcu 1 owcę z czwartego pastwiska.