Informatyczny kącik olimpijski
Jakie to proste
W tym kąciku dwa zadania z cyklu naszych ulubionych, tzn. na pierwszy rzut oka ciężkie do ugryzienia, ale mające ładne i krótkie rozwiązania.
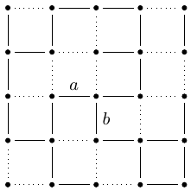
Rys. 1 Jeśli spojrzymy na mapę miasta jak na układ współrzędnych, to dla każdej pary liczb
całkowitych
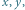 takiej że
takiej że
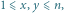 w punkcie
w punkcie
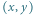 znajduje się
skrzyżowanie; ponadto każde dwa skrzyżowania oddalone o 1 są połączone ulicą.
Przykładowe miasto dla
znajduje się
skrzyżowanie; ponadto każde dwa skrzyżowania oddalone o 1 są połączone ulicą.
Przykładowe miasto dla
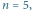 w którym zamknięto już 16 ulic (linie kropkowane). Po
zamknięciu ulicy
w którym zamknięto już 16 ulic (linie kropkowane). Po
zamknięciu ulicy
 będzie można przejechać między jej końcami, nie uda się to
natomiast po zamknięciu ulicy
będzie można przejechać między jej końcami, nie uda się to
natomiast po zamknięciu ulicy
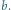
Zadanie Bajthattan pochodzi z Akademickich Mistrzostw Polski w Programowaniu Zespołowym z roku 2013.
Zadanie 1. Sieć drogowa w mieście tworzy regularną siatkę
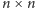 (Rys. 1). Napływają do nas informacje o zamknięciach ulic. Dla
każdej informacji mamy stwierdzić, czy po zamknięciu danej ulicy nadal
będzie można przejechać pomiędzy skrzyżowaniami położonymi na jej
końcach, poruszając się jedynie po ulicach, które dotychczas nie zostały
zamknięte.
(Rys. 1). Napływają do nas informacje o zamknięciach ulic. Dla
każdej informacji mamy stwierdzić, czy po zamknięciu danej ulicy nadal
będzie można przejechać pomiędzy skrzyżowaniami położonymi na jej
końcach, poruszając się jedynie po ulicach, które dotychczas nie zostały
zamknięte.
Oczywiście, sieć drogową możemy zastąpić grafem nieskierowanym,
w którym wierzchołki reprezentować będą skrzyżowania, a krawędzie –
ulice. I, oczywiście, rozwiązanie brutalne, które dla każdego zamknięcia
ulicy (usunięcia krawędzi grafu) wykonuje przeszukiwanie grafu w celu
znalezienia ścieżki pomiędzy dwoma wierzchołkami, nas nie satysfakcjonuje.
Takie rozwiązanie działa w czasie
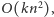 gdzie
gdzie
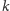 to liczba
usunięć krawędzi.
to liczba
usunięć krawędzi.
Zauważmy, że jeśli ścieżka pomiędzy końcami usuniętej krawędzi nie
istnieje, to usunięcie tej krawędzi spowodowało, że jej końce znalazły się
w różnych spójnych składowych grafu. Równoważnie zatem możemy
badać, które usunięcia krawędzi zwiększają liczbę spójnych składowych grafu.
Nasz graf jest planarny, zatem zależność między liczbą jego wierzchołków,
krawędzi, ścian (części płaszczyzny ograniczonych krawędziami) i spójnych
składowych (oznaczymy te liczby kolejno przez
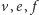 i
i
 ) wyraża
się wzorem Eulera:
) wyraża
się wzorem Eulera:

Rozważmy usunięcie jednej krawędzi. Liczba wierzchołków
 jest stała
(równa
jest stała
(równa
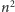 ), natomiast liczba krawędzi
), natomiast liczba krawędzi
 zmniejsza się
o jeden. Jeśli po obu stronach usuwanej krawędzi mieliśmy tę samą
ścianę, to
zmniejsza się
o jeden. Jeśli po obu stronach usuwanej krawędzi mieliśmy tę samą
ścianę, to
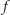 się nie zmienia (i wtedy liczba spójnych składowych
się nie zmienia (i wtedy liczba spójnych składowych
 rośnie o jeden), w przeciwnym wypadku
rośnie o jeden), w przeciwnym wypadku
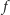 maleje o jeden
(i wtedy
maleje o jeden
(i wtedy
 się nie zmienia).
się nie zmienia).
Powyższy warunek możemy testować, trzymając ściany grafu w strukturze
dla zbiorów rozłącznych. W momencie, gdy usuwamy krawędź, dwie ściany
należy połączyć. Rozwiązanie to działa w czasie
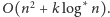
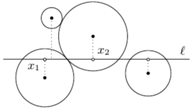
Rys. 2 Na odcinku
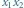 prostej
prostej
 nie ma żadnego zrzutowanego środka koła,
które przecina
nie ma żadnego zrzutowanego środka koła,
które przecina
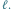
Z kolei Kręgi w zbożu pojawiły się w finale Potyczek Algorytmicznych 2012.
Zadanie. Na płaszczyźnie znajduje się
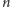 kół, których wnętrza są
rozłączne. Środek
kół, których wnętrza są
rozłączne. Środek
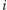 -tego koła znajduje się w punkcie
-tego koła znajduje się w punkcie
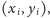 a jego promień
wynosi
a jego promień
wynosi
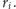 Należy wyznaczyć liczbę par kół, które mają punkt
wspólny.
Należy wyznaczyć liczbę par kół, które mają punkt
wspólny.
Znowu rozwiązanie brutalne, które z osobna sprawdza każdą
z
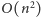 par kół, jest za wolne. Z drugiej strony, odpowiedź nie
będzie nigdy przekraczać
par kół, jest za wolne. Z drugiej strony, odpowiedź nie
będzie nigdy przekraczać
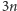 (gdyż graf o
(gdyż graf o
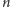 wierzchołkach
w środkach okręgów i krawędziach łączących środki stykających się kół jest
planarny, więc ma co najwyżej
wierzchołkach
w środkach okręgów i krawędziach łączących środki stykających się kół jest
planarny, więc ma co najwyżej
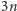 krawędzi). Spróbujmy zatem
ograniczyć liczbę kandydatów na pary, które musimy sprawdzić.
Zauważmy, że jeśli poprowadzimy linię prostą
krawędzi). Spróbujmy zatem
ograniczyć liczbę kandydatów na pary, które musimy sprawdzić.
Zauważmy, że jeśli poprowadzimy linię prostą
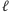 przez punkt
przecięcia pary kół, a następnie zrzutujemy prostopadle na tę prostą środki
wszystkich kół, które przecinają
przez punkt
przecięcia pary kół, a następnie zrzutujemy prostopadle na tę prostą środki
wszystkich kół, które przecinają
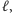 to zrzutowane środki kół
należących do pary będą sąsiadować na prostej (Rys. 2).
to zrzutowane środki kół
należących do pary będą sąsiadować na prostej (Rys. 2).
Dzięki temu spostrzeżeniu możemy zastosować metodę zamiatania.
Będziemy przesuwać od dołu do góry poziomą linię prostą (miotłę)
i jednocześnie utrzymywać zbiór kół, które ją przecinają. Zauważmy, że
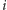 -te koło zostanie wrzucone do zbioru, gdy miotła będzie w pozycji
-te koło zostanie wrzucone do zbioru, gdy miotła będzie w pozycji
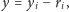 a zostanie z niego usunięte dla
a zostanie z niego usunięte dla
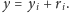 Co więcej,
będą to jedyne momenty, w których zawartość zbioru będzie się zmieniać.
Zatem w czasie
Co więcej,
będą to jedyne momenty, w których zawartość zbioru będzie się zmieniać.
Zatem w czasie
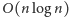 sortujemy te „istotne” pozycje miotły,
a następnie przechodzimy je w kolejności niemalejącej. Za każdym razem,
gdy uaktualnimy zbiór, sprawdzamy stałą liczbę par kół (konkretnie te, które
sąsiadują z dodanym kołem lub sąsiadowały z usuniętym). Zbiór realizujemy
jako uporządkowany słownik, w którym koła są posortowane względem
wartości
sortujemy te „istotne” pozycje miotły,
a następnie przechodzimy je w kolejności niemalejącej. Za każdym razem,
gdy uaktualnimy zbiór, sprawdzamy stałą liczbę par kół (konkretnie te, które
sąsiadują z dodanym kołem lub sąsiadowały z usuniętym). Zbiór realizujemy
jako uporządkowany słownik, w którym koła są posortowane względem
wartości
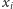 i który umożliwia w czasie
i który umożliwia w czasie
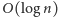 dodawanie
i usuwanie elementów oraz znajdowanie następnego i poprzedniego elementu
w tym porządku.
dodawanie
i usuwanie elementów oraz znajdowanie następnego i poprzedniego elementu
w tym porządku.
Rozwiązanie działa w czasie
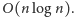 I jak to bywa w zadaniach
z geometrii obliczeniowej – pozostał jeden przypadek szczególny (gdy miotła
jest styczna do pary kół), którego uwzględnienie pozostawiamy jako zadanie dla
Czytelników.
I jak to bywa w zadaniach
z geometrii obliczeniowej – pozostał jeden przypadek szczególny (gdy miotła
jest styczna do pary kół), którego uwzględnienie pozostawiamy jako zadanie dla
Czytelników.
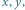 takiej że
takiej że
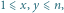 w punkcie
w punkcie
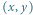 znajduje się
skrzyżowanie; ponadto każde dwa skrzyżowania oddalone o 1 są połączone ulicą.
Przykładowe miasto dla
znajduje się
skrzyżowanie; ponadto każde dwa skrzyżowania oddalone o 1 są połączone ulicą.
Przykładowe miasto dla
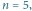 w którym zamknięto już 16 ulic (linie kropkowane). Po
zamknięciu ulicy
w którym zamknięto już 16 ulic (linie kropkowane). Po
zamknięciu ulicy
 będzie można przejechać między jej końcami, nie uda się to
natomiast po zamknięciu ulicy
będzie można przejechać między jej końcami, nie uda się to
natomiast po zamknięciu ulicy
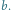
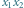 prostej
prostej
 nie ma żadnego zrzutowanego środka koła,
które przecina
nie ma żadnego zrzutowanego środka koła,
które przecina