Informatyczny kącik olimpijski
Palindromy
W tym kąciku informatycznym – zadanie Palindromy z finału XIII Olimpiady Informatycznej.
Zadanie. Mamy
danych
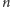 różnych palindromów (czyli słów, które są takie same
czytane od początku, jak i od końca) złożonych z małych liter alfabetu
angielskiego (a więc mamy co najwyżej
różnych palindromów (czyli słów, które są takie same
czytane od początku, jak i od końca) złożonych z małych liter alfabetu
angielskiego (a więc mamy co najwyżej
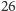 różnych liter). Wiemy,
że sumaryczna długość wszystkich palindromów jest nie większa niż
różnych liter). Wiemy,
że sumaryczna długość wszystkich palindromów jest nie większa niż
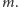 Pytanie jest następujące: ile jest różnych par (uporządkowanych)
podanych palindromów, które sklejone dają także palindrom?
Pytanie jest następujące: ile jest różnych par (uporządkowanych)
podanych palindromów, które sklejone dają także palindrom?
Na początku wprowadźmy kilka oznaczeń. Jeśli
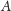 jest słowem, to
przez
jest słowem, to
przez
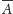 oznaczymy
oznaczymy
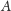 czytane od tyłu. Zatem
czytane od tyłu. Zatem
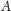 jest
palindromem, jeśli
jest
palindromem, jeśli
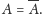 Dalej, przez
Dalej, przez
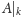 oznaczymy
prefiks
oznaczymy
prefiks
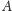 o długości
o długości
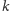 (a więc pierwsze
(a więc pierwsze
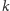 liter słowa
liter słowa
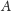 ), za to przez
), za to przez
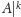 – sufiks
– sufiks
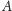 o długości
o długości
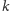 (tj.
(tj.
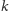 ostatnich liter
ostatnich liter
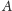 ). I jeszcze, niech
). I jeszcze, niech
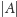 będzie długością
słowa
będzie długością
słowa
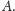
Zacznijmy od kilku spostrzeżeń, które narzucają się po przeanalizowaniu
choćby przykładu do tego zadania – Czytelnikowi proponuję rozpisanie
własnego i przyjrzenie mu się. Po pierwsze, na pewno każdy palindrom
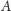 z wejścia zwiększa wynik co najmniej o
z wejścia zwiększa wynik co najmniej o
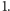 Jest tak
dlatego, że skoro
Jest tak
dlatego, że skoro
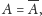 to
to
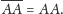 Po drugie, niech
Po drugie, niech
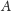 i
i
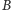 będą takimi palindromami, że
będą takimi palindromami, że
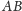 też jest
palindromem, oraz niech
też jest
palindromem, oraz niech
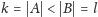 (zachodzi albo to, albo
nierówność w drugą stronę – długości nie mogą być sobie równe,
bo wtedy mielibyśmy
(zachodzi albo to, albo
nierówność w drugą stronę – długości nie mogą być sobie równe,
bo wtedy mielibyśmy
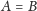 ). Wtedy
). Wtedy
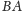 również jest
palindromem. Faktycznie, zachodzi
również jest
palindromem. Faktycznie, zachodzi
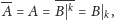 a ponadto
a ponadto
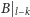 jest palindromem, więc
jest palindromem, więc
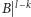 również. Łatwo zauważyć,
że występuje tutaj równoważność, czyli jeśli
również. Łatwo zauważyć,
że występuje tutaj równoważność, czyli jeśli
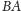 jest palindromem,
to
jest palindromem,
to
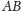 również.
również.
Sumarycznym wynikiem jest więc
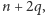 gdzie
gdzie
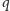 to liczba takich
par różnych palindromów
to liczba takich
par różnych palindromów
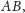 że
że
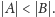
No to teraz możemy zastanowić się nad tym, kiedy dwa palindromy
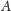 i
i
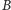
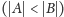 tworzą palindrom
tworzą palindrom
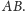 Na pewno
trzeba, żeby
Na pewno
trzeba, żeby
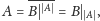 czyli żeby
czyli żeby
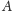 było prefiksem
było prefiksem
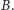 Poza tym jeszcze
Poza tym jeszcze
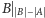 musi być palindromem (jest to
środek
musi być palindromem (jest to
środek
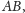 po ucięciu z początku i z końca
po ucięciu z początku i z końca
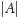 liter). Na bazie
tych dwóch warunków zbudujemy już rozwiązanie zadania.
liter). Na bazie
tych dwóch warunków zbudujemy już rozwiązanie zadania.
Zacznijmy od tego, jak znaleźć wszystkie palindromy
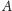 z wejścia, będące
prefiksami palindromu
z wejścia, będące
prefiksami palindromu
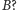 Załóżmy, że wejście jest posortowane
leksykograficznie. Zauważmy, że jeśli
Załóżmy, że wejście jest posortowane
leksykograficznie. Zauważmy, że jeśli
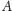 jest prefiksem
jest prefiksem
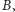 to
w kolejności leksykograficznej między nimi mogą znaleźć się tylko takie
słowa
to
w kolejności leksykograficznej między nimi mogą znaleźć się tylko takie
słowa
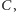 że
że
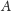 jest prefiksem
jest prefiksem
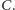 Załóżmy, że mamy
policzoną listę
Załóżmy, że mamy
policzoną listę
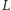 wszystkich spośród naszych palindromów, które są
prefiksami
wszystkich spośród naszych palindromów, które są
prefiksami
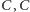 występuje bezpośrednio przed
występuje bezpośrednio przed
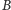 w kolejności
leksykograficznej oraz znamy maksymalne możliwe
w kolejności
leksykograficznej oraz znamy maksymalne możliwe
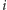 spełniające
spełniające
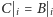 (obliczenie takiego
(obliczenie takiego
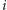 to koszt
to koszt
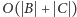 ). Wtedy
lista wszystkich spośród naszych słów, które są prefiksami
). Wtedy
lista wszystkich spośród naszych słów, które są prefiksami
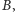 to lista
to lista
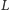 uzupełniona o
uzupełniona o
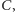 z której zostały usunięte wszystkie słowa
dłuższe niż
z której zostały usunięte wszystkie słowa
dłuższe niż
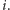 Długość tej listy dla
Długość tej listy dla
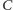 jest ograniczona przez
długość
jest ograniczona przez
długość
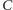 (na wejściu mamy parami różne palindromy), a więc
cała operacja otrzymania listy dla
(na wejściu mamy parami różne palindromy), a więc
cała operacja otrzymania listy dla
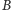 z listy dla
z listy dla
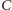 ma koszt
ma koszt
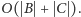
W drugim kroku chcielibyśmy sprawdzić, dla danej pary palindromów
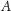 i
i
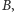 gdzie
gdzie
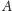 występuje na liście odpowiadającej
występuje na liście odpowiadającej
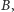 czy rzeczywiście
czy rzeczywiście
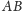 jest palindromem, czyli czy
jest palindromem, czyli czy
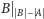 też nim jest.
też nim jest.
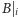 jest palindromem wtedy i tylko wtedy,
gdy
jest palindromem wtedy i tylko wtedy,
gdy
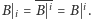
A w takim razie
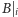 musi być jednocześnie i prefiksem, i sufiksem
słowa
musi być jednocześnie i prefiksem, i sufiksem
słowa
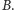 A to już brzmi znajomo – w tym momencie warto skorzystać
z algorytmu Knutha–Morrisa–Pratta (Czytelnikowi nieobeznanemu z tym
algorytmem polecam skorzystanie z mnóstwa materiałów dostępnych
w Internecie). W tym algorytmie wyznaczana jest tablica prefiksowa
A to już brzmi znajomo – w tym momencie warto skorzystać
z algorytmu Knutha–Morrisa–Pratta (Czytelnikowi nieobeznanemu z tym
algorytmem polecam skorzystanie z mnóstwa materiałów dostępnych
w Internecie). W tym algorytmie wyznaczana jest tablica prefiksowa
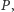 w której
w której
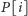 jest długością najdłuższego prefiksu, będącego
jednocześnie sufiksem słowa
jest długością najdłuższego prefiksu, będącego
jednocześnie sufiksem słowa
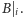 Zauważmy, że długością
najdłuższego prefiksu, będącego jednocześnie sufiksem
Zauważmy, że długością
najdłuższego prefiksu, będącego jednocześnie sufiksem
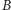 jest
jest
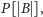 następnego najdłuższego –
następnego najdłuższego –
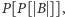 itd., aż
w końcu
itd., aż
w końcu
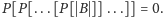 Algorytm KMP oblicza tablicę
Algorytm KMP oblicza tablicę
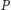 w czasie
w czasie
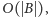 a my w takim samym czasie możemy
odczytać z niej długości wszystkich prefiksów
a my w takim samym czasie możemy
odczytać z niej długości wszystkich prefiksów
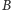 będących sufiksami
będących sufiksami
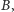 czyli palindromami. Po tych wstępnych obliczeniach można już
natychmiastowo sprawdzić, dla każdego palindromu
czyli palindromami. Po tych wstępnych obliczeniach można już
natychmiastowo sprawdzić, dla każdego palindromu
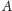 z listy
odpowiadającej
z listy
odpowiadającej
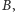 czy
czy
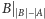 jest palindromem.
jest palindromem.
W takim razie sumaryczny czas, jaki musimy poświęcić
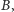 jest rzędu
jest rzędu
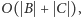 gdzie
gdzie
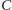 jest poprzednim leksykograficznie
palindromem, a więc sumaryczny czas całego algorytmu, nie licząc sortowania,
to
jest poprzednim leksykograficznie
palindromem, a więc sumaryczny czas całego algorytmu, nie licząc sortowania,
to
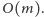 Czytelnikowi pozostawiam sprytną implementację algorytmu
sortowania pozycyjnego tak, żeby złożoność całego algorytmu pozostała
Czytelnikowi pozostawiam sprytną implementację algorytmu
sortowania pozycyjnego tak, żeby złożoność całego algorytmu pozostała
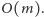 Liczba „obrotów” sortowania może być bliska
Liczba „obrotów” sortowania może być bliska
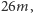 ze
względu na rozmiar alfabetu – chociaż tę stałą da się znacząco zmniejszyć, co
również polecam jako ćwiczenie.
ze
względu na rozmiar alfabetu – chociaż tę stałą da się znacząco zmniejszyć, co
również polecam jako ćwiczenie.