Informatyczny kącik olimpijski
Multizbiory
W tym kąciku proponuję zadanie polecane przez mojego korespondenta w Jekaterynburgu, mieście znanym również z turnieju Ural Sport Programming Championship, którego zeszłoroczną atrakcją był bezwzględny pojedynek pięciu najlepszych drużyn z Rosji z pięcioma najlepszymi drużynami z Chin. Popatrzmy na zadanie, którego nie udało się rozwiązać żadnej z nich!
Mamy dany ciąg liczb
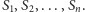 Rozważamy jego wszystkie spójne
podciągi, czyli fragmenty postaci
Rozważamy jego wszystkie spójne
podciągi, czyli fragmenty postaci
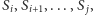 które sortujemy
w dość dziwny sposób. Mianowicie, aby porównać dwa fragmenty
które sortujemy
w dość dziwny sposób. Mianowicie, aby porównać dwa fragmenty
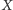 i
i
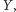 szukamy najmniejszej liczby
szukamy najmniejszej liczby
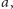 która występuje
różną liczbę razy w
która występuje
różną liczbę razy w
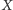 i
i
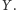 Fragment
Fragment
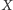 jest mniejszy
niż
jest mniejszy
niż
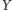 (co zapisujemy jako
(co zapisujemy jako
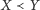 ) dokładnie wtedy, gdy owa
liczba
) dokładnie wtedy, gdy owa
liczba
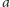 występuje więcej razy w
występuje więcej razy w
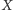 niż w
niż w
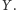 Jeśli
takiej liczby nie ma, to fragmenty są dla nas takie same; innymi słowy
porównujemy multizbiory liczb występujące w obu fragmentach. Naszym
zadaniem jest wyznaczenie multizbioru, który jest generowany przez
Jeśli
takiej liczby nie ma, to fragmenty są dla nas takie same; innymi słowy
porównujemy multizbiory liczb występujące w obu fragmentach. Naszym
zadaniem jest wyznaczenie multizbioru, który jest generowany przez
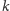 -ty
fragment w tym dziwnym porządku.
-ty
fragment w tym dziwnym porządku.
Pewnie warto przez chwilę zwątpić, czy ten porządek jest faktycznie porządkiem,
czyli czy
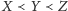 implikuje, że
implikuje, że
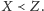 W przeciwnym
przypadku ciężko byłoby bowiem mówić o sortowaniu. Na szczęście,
okazuje się, że tak jest w istocie (
W przeciwnym
przypadku ciężko byłoby bowiem mówić o sortowaniu. Na szczęście,
okazuje się, że tak jest w istocie (
 jest w rzeczywistości porządkiem
leksykograficznym na fragmentach potraktowanych jako multizbiory).
Ograniczenia podane w treści to
jest w rzeczywistości porządkiem
leksykograficznym na fragmentach potraktowanych jako multizbiory).
Ograniczenia podane w treści to
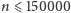 i
i
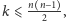 czyli
wygenerowanie i posortowanie wszystkich fragmentów nie jest najlepszym
z możliwych pomysłów. Ba, problematyczne byłoby już nawet samo
wygenerowanie fragmentów, nie mówiąc o tym, że porównanie dwóch
fragmentów wydaje się wymagać czasu proporcjonalnego do ich długości.
Zaczyna się robić ciekawie!
czyli
wygenerowanie i posortowanie wszystkich fragmentów nie jest najlepszym
z możliwych pomysłów. Ba, problematyczne byłoby już nawet samo
wygenerowanie fragmentów, nie mówiąc o tym, że porównanie dwóch
fragmentów wydaje się wymagać czasu proporcjonalnego do ich długości.
Zaczyna się robić ciekawie!
Co prawda, interesuje nas wyznaczenie
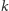 -tego fragmentu, ale może
wypadałoby urealnić oczekiwania i zacząć od próby skonstruowania
efektywnego sposobu zliczania fragmentów, które są ściśle mniejsze
od danego? Jest to dość standardowe podejście: zamiast rozwiązywać problem
„znajdź najmniejsze dobre rozwiązanie”, zajmujemy się problemem„sprawdź,
czy dane rozwiązanie jest dobre”. Potem zwykle wystarczy tylko zastosować
wyszukiwanie binarne, choć w naszym przypadku sytuacja okaże się odrobinę
bardziej skomplikowana.
-tego fragmentu, ale może
wypadałoby urealnić oczekiwania i zacząć od próby skonstruowania
efektywnego sposobu zliczania fragmentów, które są ściśle mniejsze
od danego? Jest to dość standardowe podejście: zamiast rozwiązywać problem
„znajdź najmniejsze dobre rozwiązanie”, zajmujemy się problemem„sprawdź,
czy dane rozwiązanie jest dobre”. Potem zwykle wystarczy tylko zastosować
wyszukiwanie binarne, choć w naszym przypadku sytuacja okaże się odrobinę
bardziej skomplikowana.
Mając dany fragment
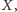 chcemy zliczyć fragmenty
chcemy zliczyć fragmenty
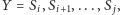 dla których
dla których
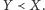 Dość naturalne jest
ustalenie
Dość naturalne jest
ustalenie
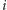 i przyjrzenie się wszystkim
i przyjrzenie się wszystkim
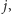 które spełniają żądany
warunek. Po chwili namysłu można dostrzec, że dodając kolejne elementy,
możemy tylko zmniejszyć
które spełniają żądany
warunek. Po chwili namysłu można dostrzec, że dodając kolejne elementy,
możemy tylko zmniejszyć
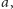 które ma więcej wystąpień, zatem
które ma więcej wystąpień, zatem
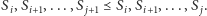 Wynika stąd, że
Wynika stąd, że
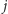 spełniające
warunek tworzą spójny przedział
spełniające
warunek tworzą spójny przedział
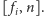 Ale jak wyznaczyć
to
Ale jak wyznaczyć
to
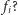 Pewnie moglibyśmy zacząć od
Pewnie moglibyśmy zacząć od
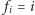 i zwiększać je
o jeden, dopóki
i zwiększać je
o jeden, dopóki
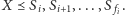 Brzmi to całkiem rozsądnie, choć
pojawiają się co najmniej dwa problemy. Przede wszystkim potrzebujemy
efektywnej metody na sprawdzanie, czy aktualne
Brzmi to całkiem rozsądnie, choć
pojawiają się co najmniej dwa problemy. Przede wszystkim potrzebujemy
efektywnej metody na sprawdzanie, czy aktualne
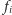 należy zwiększyć
o jeden. Jest to jednak dość łatwe: trzeba tylko skonstruować strukturę danych,
która umożliwi nam przechowywanie dla każdego
należy zwiększyć
o jeden. Jest to jednak dość łatwe: trzeba tylko skonstruować strukturę danych,
która umożliwi nam przechowywanie dla każdego
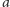 różnicy
między liczbą jego wystąpień w
różnicy
między liczbą jego wystąpień w
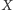 i liczbą jego wystąpień w aktualnym
fragmencie
i liczbą jego wystąpień w aktualnym
fragmencie
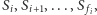 oraz znajdowanie najmniejszego
oraz znajdowanie najmniejszego
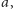 dla
którego ta różnica nie jest zerem. Musi również umożliwiać dodawanie
nowych elementów
dla
którego ta różnica nie jest zerem. Musi również umożliwiać dodawanie
nowych elementów
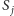 (co wiąże się ze zmniejszaniem odpowiadających
im różnic). Taką strukturą może być zwykłe drzewo licznikowe,
które umożliwia wykonywanie zarówno aktualizacji, jak i pytań
w czasie
(co wiąże się ze zmniejszaniem odpowiadających
im różnic). Taką strukturą może być zwykłe drzewo licznikowe,
które umożliwia wykonywanie zarówno aktualizacji, jak i pytań
w czasie
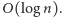 Dysponując takim narzędziem, będziemy w stanie
wyznaczyć każde
Dysponując takim narzędziem, będziemy w stanie
wyznaczyć każde
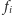 w czasie
w czasie
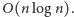 Niby fajnie,
ale w tym momencie pojawia się drugi problem: przecież mamy aż
Niby fajnie,
ale w tym momencie pojawia się drugi problem: przecież mamy aż
 różnych
różnych
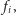 które wypadałoby znaleźć! Na szczęście
można zauważyć, że
które wypadałoby znaleźć! Na szczęście
można zauważyć, że
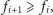 czyli dla kolejnego
czyli dla kolejnego
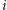 możemy
zacząć od
możemy
zacząć od
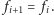 Jest to o tyle wygodne, że wspomniane przed
chwilą drzewo licznikowe bez większych problemów pozwala także na
zwiększenie
Jest to o tyle wygodne, że wspomniane przed
chwilą drzewo licznikowe bez większych problemów pozwala także na
zwiększenie
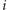 o jeden (czyli na usunięcie
o jeden (czyli na usunięcie
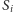 z aktualnego
fragmentu). Zatem dla kolejnych
z aktualnego
fragmentu). Zatem dla kolejnych
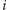 zwiększamy
zwiększamy
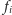 o jeden tak
długo, jak aktualny fragment jest nie mniejszy niż
o jeden tak
długo, jak aktualny fragment jest nie mniejszy niż
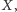 a następnie
usuwamy
a następnie
usuwamy
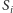 ze struktury. Ponieważ
ze struktury. Ponieważ
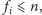 wykonamy
nie więcej niż
wykonamy
nie więcej niż
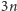 operacji na drzewie licznikowym, co daje sumaryczny
czas
operacji na drzewie licznikowym, co daje sumaryczny
czas
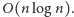 Fantastycznie.
Fantastycznie.
Umiemy więc obliczyć, ile fragmentów jest mniejszych od
danego
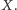 Używając bardzo podobnej metody, można też zliczyć
fragmenty, które są równe
Używając bardzo podobnej metody, można też zliczyć
fragmenty, które są równe
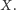 O ile więc tylko ktoś podrzuciłby nam
fragment
O ile więc tylko ktoś podrzuciłby nam
fragment
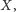 umielibyśmy sprawdzić, czy faktycznie jest on
umielibyśmy sprawdzić, czy faktycznie jest on
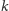 -tym w naszym porządku (jeśli mamy
-tym w naszym porządku (jeśli mamy
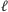 fragmentów, które są
mniejsze od
fragmentów, które są
mniejsze od
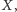 i
i
 takich, które są równe
takich, które są równe
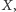 wystarczy
sprawdzić czy
wystarczy
sprawdzić czy
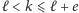 ). Niestety, nie mamy co liczyć na żadną
życzliwą podpowiedź.
). Niestety, nie mamy co liczyć na żadną
życzliwą podpowiedź.
Spróbujemy zastosować strategię przypominającą wyszukiwanie binarne.
Na dobry początek możemy stwierdzić, że szukany fragment na pewno znajduje
się (w zdefiniowanym wyżej porządku) między
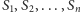 a (dowolnym)
pustym fragmentem. Załóżmy więc, że wiemy już, iż szukany
a (dowolnym)
pustym fragmentem. Załóżmy więc, że wiemy już, iż szukany
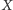 leży
między fragmentami
leży
między fragmentami
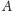 a
a
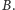 Co dalej? Przydałby nam się
fragment
Co dalej? Przydałby nam się
fragment
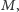 który leży mniej więcej w połowie drogi między
który leży mniej więcej w połowie drogi między
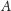 a
a
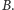 Mając
Mając
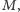 moglibyśmy szybko zliczyć fragmenty,
które są od niego mniejsze, porównać tę liczbę z
moglibyśmy szybko zliczyć fragmenty,
które są od niego mniejsze, porównać tę liczbę z
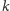 i w zależności
od wyniku zastąpić
i w zależności
od wyniku zastąpić
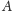 lub
lub
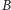 przez
przez
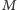 (lub stwierdzić,
że właśnie
(lub stwierdzić,
że właśnie
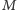 jest szukanym fragmentem). Dobranie się
do takiego
jest szukanym fragmentem). Dobranie się
do takiego
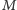 wydaje się jednak dość problematyczne, gdyż zakłada,
że znamy cały porządek na fragmentach, a przecież tak nie jest.
wydaje się jednak dość problematyczne, gdyż zakłada,
że znamy cały porządek na fragmentach, a przecież tak nie jest.
Wyobraźmy sobie zbiór wszystkich fragmentów, które leżą (w naszym dziwnym
porządku) między
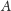 a
a
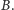 Dla każdego
Dla każdego
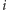 prawe końce
takich
prawe końce
takich
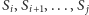 tworzą spójny przedział
tworzą spójny przedział
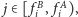 co więcej,
używając opisanej wyżej metody, możemy efektywnie wyznaczyć
wszystkie
co więcej,
używając opisanej wyżej metody, możemy efektywnie wyznaczyć
wszystkie
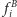 i
i
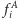 (po prostu rozważamy wszystkie fragmenty
mniejsze niż
(po prostu rozważamy wszystkie fragmenty
mniejsze niż
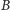 i odrzucamy te, które są również mniejsze
niż
i odrzucamy te, które są również mniejsze
niż
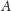 ). Można więc przedstawić interesujący nas zbiór jako
sumę
). Można więc przedstawić interesujący nas zbiór jako
sumę
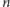 mniejszych zbiorów
mniejszych zbiorów
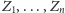 (każdy z nich
jest tak naprawdę posortowany, choć nie będzie to dla nas istotne).
Ale co z tego?
(każdy z nich
jest tak naprawdę posortowany, choć nie będzie to dla nas istotne).
Ale co z tego?
Skoro nie wiemy, co zrobić, może warto wpaść w panikę i zrobić coś
losowego. Spróbujmy więc wybrać losowy spośród fragmentów, które
leżą między
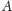 a
a
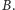 Wystarczy tylko wylosować jeden ze
zbiorów
Wystarczy tylko wylosować jeden ze
zbiorów
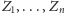 (jako że ich rozmiary mogą być dość różne,
to wybieramy
(jako że ich rozmiary mogą być dość różne,
to wybieramy
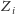 z prawdopodobieństwem
z prawdopodobieństwem
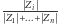 ),
a następnie element w zbiorze. Wylosowawszy fragment
),
a następnie element w zbiorze. Wylosowawszy fragment
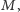 możemy
sprawdzić, czy szukany fragment jest mniejszy czy większy (a może równy)
od
możemy
sprawdzić, czy szukany fragment jest mniejszy czy większy (a może równy)
od
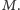 A dlaczego to działa?
A dlaczego to działa?
Wybierając losowy element, mamy sporą szansę, że liczba elementów między
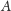 a
a
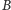 istotnie się zmniejszy. Najłatwiej wyobrazić sobie sytuację,
korzystając z poniższej ilustracji, na której kolejne kropki reprezentują
elementy między
istotnie się zmniejszy. Najłatwiej wyobrazić sobie sytuację,
korzystając z poniższej ilustracji, na której kolejne kropki reprezentują
elementy między
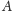 a
a
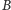 ułożone w kolejności zgodnej
z naszym dziwnym porządkiem. Powiedzmy, że jest ich
ułożone w kolejności zgodnej
z naszym dziwnym porządkiem. Powiedzmy, że jest ich
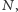 a szukany
element to kolorowa kropka na pozycji
a szukany
element to kolorowa kropka na pozycji
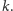 Skoro wybieramy losowy
element, to z prawdopodobieństwem
Skoro wybieramy losowy
element, to z prawdopodobieństwem
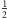 będzie on w środkowym
okienku długości
będzie on w środkowym
okienku długości
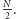 Tak naprawdę sprawdzamy, czy wybrany element
jest na prawo czy na lewo od szukanego, i w zależności od wyniku
porównania pozbywamy się elementów na lewo lub na prawo od tego
losowo wybranego. A to jest bardzo wygodne: zawsze pozbędziemy się
przynajmniej lewego lub prawego kawałka długości
Tak naprawdę sprawdzamy, czy wybrany element
jest na prawo czy na lewo od szukanego, i w zależności od wyniku
porównania pozbywamy się elementów na lewo lub na prawo od tego
losowo wybranego. A to jest bardzo wygodne: zawsze pozbędziemy się
przynajmniej lewego lub prawego kawałka długości
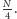 Czyli
mamy przynajmniej
Czyli
mamy przynajmniej
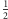 szansy na to, że liczba elementów między
szansy na to, że liczba elementów między
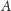 a
a
 spadnie przynajmniej o jedną czwartą.
spadnie przynajmniej o jedną czwartą.
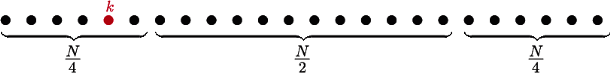
Skoro zaczynamy z
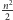 kandydatami, szansa na to, że konieczne okaże
się dużo więcej niż, powiedzmy,
kandydatami, szansa na to, że konieczne okaże
się dużo więcej niż, powiedzmy,
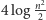 iteracji, wydaje się niewielka.
Darujemy sobie szczegółowe rachunki, wymagają one bowiem pewnej
elementarnej wiedzy z rachunku prawdopodobieństwa: uwierzcie mi, że
oczekiwana liczba rund to
iteracji, wydaje się niewielka.
Darujemy sobie szczegółowe rachunki, wymagają one bowiem pewnej
elementarnej wiedzy z rachunku prawdopodobieństwa: uwierzcie mi, że
oczekiwana liczba rund to
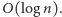 Otrzymaliśmy więc rozwiązanie
o oczekiwanym czasie działania
Otrzymaliśmy więc rozwiązanie
o oczekiwanym czasie działania
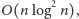 które w dodatku nie jest
bardzo skomplikowane implementacyjnie.
które w dodatku nie jest
bardzo skomplikowane implementacyjnie.