Informatyczny kącik olimpijski
Różne słowa
W tym kąciku omówimy zadanie Różne słowa z Obozu Naukowo-Treningowego im. A. Kreczmara w 2013 roku.
Zadanie. Dane jest
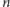 słów o długości
słów o długości
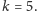 Słowa
składają się z małych i wielkich liter alfabetu łacińskiego. Naszym zadaniem
jest stwierdzić, czy istnieje wśród nich para kompletnie różnych słów,
czyli słów, które na odpowiadających sobie pozycjach mają różne litery.
Słowa
składają się z małych i wielkich liter alfabetu łacińskiego. Naszym zadaniem
jest stwierdzić, czy istnieje wśród nich para kompletnie różnych słów,
czyli słów, które na odpowiadających sobie pozycjach mają różne litery.
Słowa
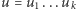 i
i
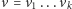 są więc kompletnie różne, jeśli
są więc kompletnie różne, jeśli
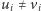 dla każdego
dla każdego
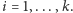 Mimo prostego sformułowania
rozwiązanie zadania wymaga pewnej pomysłowości. Przedstawimy dwa różne
podejścia do rozwiązania.
Mimo prostego sformułowania
rozwiązanie zadania wymaga pewnej pomysłowości. Przedstawimy dwa różne
podejścia do rozwiązania.
Pierwszy pomysł będzie opierał się na zasadzie włączeń-wyłączeń. W pierwszym
kroku dla każdego słowa wyznaczymy wszystkie wzorce, do których ono
pasuje. Wzorcem nazywamy tutaj słowo długości
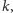 które oprócz liter
może zawierać znaki zapytania – znak zapytania zastępuje we wzorcu dowolną
literę. Przykładowo, ze słowa abcab można otrzymać m.in. wzorce
a?c?? i ????b. Zastępując każdą możliwą kombinację liter w słowie
znakami zapytania, dla jednego słowa otrzymamy
które oprócz liter
może zawierać znaki zapytania – znak zapytania zastępuje we wzorcu dowolną
literę. Przykładowo, ze słowa abcab można otrzymać m.in. wzorce
a?c?? i ????b. Zastępując każdą możliwą kombinację liter w słowie
znakami zapytania, dla jednego słowa otrzymamy
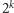 różnych
wzorców. Wszystkie te informacje możemy następnie połączyć w jedną
tabelę, która dla każdego wzorca zapamięta liczbę wejściowych słów
pasujących do niego. Ze względu na konieczność posortowania par:
wzorzec-słowo złożoność czasowa konstrukcji takiej tabeli wyniesie
różnych
wzorców. Wszystkie te informacje możemy następnie połączyć w jedną
tabelę, która dla każdego wzorca zapamięta liczbę wejściowych słów
pasujących do niego. Ze względu na konieczność posortowania par:
wzorzec-słowo złożoność czasowa konstrukcji takiej tabeli wyniesie
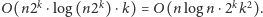
Zaopatrzeni w tabelę wzorców możemy już zastosować zasadę
włączeń-wyłączeń. Dla każdego z wejściowych słów chcemy wyznaczyć
liczbę par kompletnie różnych słów, w skład których to słowo wchodzi.
Ustalmy jedno słowo wejściowe
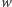 i oznaczmy przez
i oznaczmy przez
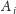 liczbę
wejściowych słów, które zgadzają się ze słowem
liczbę
wejściowych słów, które zgadzają się ze słowem
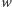 na
na
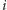 -tej
pozycji
-tej
pozycji
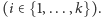 Wówczas wynik dla słowa
Wówczas wynik dla słowa
 możemy
obliczyć ze wzoru:
możemy
obliczyć ze wzoru:

Zauważmy, że składnik
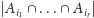 w powyższej sumie
odpowiada liczbie słów wejściowych pasujących do wzorca powstałego
z
w powyższej sumie
odpowiada liczbie słów wejściowych pasujących do wzorca powstałego
z
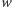 poprzez zastąpienie liter na wszystkich indeksach poza
poprzez zastąpienie liter na wszystkich indeksach poza
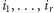 znakami zapytania. Liczbę takich słów możemy odczytać
bezpośrednio z tabeli wzorców. Łączny koszt drugiej fazy rozwiązania to
znakami zapytania. Liczbę takich słów możemy odczytać
bezpośrednio z tabeli wzorców. Łączny koszt drugiej fazy rozwiązania to
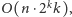 jest on zdominowany przez koszt pierwszej fazy. Zauważmy,
że opisane rozwiązanie pozwala nie tylko stwierdzić, czy wśród podanych
słów jest jakaś para kompletnie różnych słów, lecz także wyznaczyć liczbę
takich par.
jest on zdominowany przez koszt pierwszej fazy. Zauważmy,
że opisane rozwiązanie pozwala nie tylko stwierdzić, czy wśród podanych
słów jest jakaś para kompletnie różnych słów, lecz także wyznaczyć liczbę
takich par.
Drugie rozwiązanie koncentruje się na alfabecie, czyli na zbiorze liter
występujących w słowach. W naszym zadaniu alfabet ma
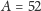 litery.
Zastanówmy się, co by było, gdybyśmy mieli do czynienia z dużo
mniejszym alfabetem: alfabetem dwuliterowym. Wówczas mielibyśmy tylko
litery.
Zastanówmy się, co by było, gdybyśmy mieli do czynienia z dużo
mniejszym alfabetem: alfabetem dwuliterowym. Wówczas mielibyśmy tylko
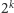 różnych słów i dla każdego słowa umielibyśmy wskazać jedyne
słowo, które tworzyłoby z nim parę kompletnie różnych słów; byłoby to
słowo stanowiące „negację” pierwszego. Rozwiązanie zadania w tym
przypadku nie przedstawiałoby żadnych trudności. W naszym zadaniu nie
mamy do czynienia z tak prostym przypadkiem. Spróbujemy jednak
sprowadzić je do tego przypadku, wprowadzając do rozwiązania element
losowości.
różnych słów i dla każdego słowa umielibyśmy wskazać jedyne
słowo, które tworzyłoby z nim parę kompletnie różnych słów; byłoby to
słowo stanowiące „negację” pierwszego. Rozwiązanie zadania w tym
przypadku nie przedstawiałoby żadnych trudności. W naszym zadaniu nie
mamy do czynienia z tak prostym przypadkiem. Spróbujemy jednak
sprowadzić je do tego przypadku, wprowadzając do rozwiązania element
losowości.
Każdej literze alfabetu przyporządkujemy losowo bit 0 lub 1. Co więcej,
uczynimy to osobno dla każdej pozycji w słowach, przy czym losowania na
poszczególnych pozycjach będą niezależne. W ten sposób sprowadzimy
zadanie do przypadku binarnego, lecz, niestety, utracimy pewien zasób
informacji. Dokładniej, wiemy, że jeśli po tym przyporządkowaniu jakieś dwa
słowa są wzajemnie negacjami, to przed zamianą liter były one kompletnie
różne, jednak implikacja odwrotna nie musi zachodzić. Zastanówmy się,
jakie jest prawdopodobieństwo tego, że dana para kompletnie różnych słów
przeszła na parę słów będących wzajemnie negacjami. W przypadku jednej
pozycji jest ono równe
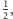 gdyż taka jest szansa na to, że dwie ustalone
różne litery oryginalnego alfabetu otrzymały w losowaniu różne bity.
Ponieważ losowania na poszczególnych pozycjach były niezależne, więc
szukane prawdopodobieństwo z uwzględnieniem wszystkich pozycji jest
równe
gdyż taka jest szansa na to, że dwie ustalone
różne litery oryginalnego alfabetu otrzymały w losowaniu różne bity.
Ponieważ losowania na poszczególnych pozycjach były niezależne, więc
szukane prawdopodobieństwo z uwzględnieniem wszystkich pozycji jest
równe
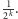
Aby zwiększyć nasze szanse, możemy całe losowanie wielokrotnie
powtórzyć. Szansa na to, że po wykonaniu
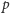 prób dane dwa
kompletnie różne słowa ani razu nie okażą się wzajemnie negacjami, wynosi
prób dane dwa
kompletnie różne słowa ani razu nie okażą się wzajemnie negacjami, wynosi
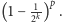 Jeśli zatem wykonamy
Jeśli zatem wykonamy
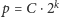 losowań, gdzie
losowań, gdzie
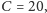 prawdopodobieństwo porażki będzie znikome:
prawdopodobieństwo porażki będzie znikome:

Złożoność całego rozwiązania wynosi
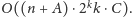 Za
pomocą tego samego podejścia można bez problemu wyznaczyć jakieś
Za
pomocą tego samego podejścia można bez problemu wyznaczyć jakieś
 par kompletnie różnych słów z wejścia (lub wszystkie takie pary,
jeśli jest ich mniej niż
par kompletnie różnych słów z wejścia (lub wszystkie takie pary,
jeśli jest ich mniej niż
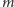 ), czego wymagało oryginalne polecenie
omawianego zadania.
), czego wymagało oryginalne polecenie
omawianego zadania.