Bardzo oszczędne drzewa (II)
Skoro dotychczas szło nam tak dobrze, spróbujmy pójść za ciosem i zaproponować bardzo oszczędną reprezentację drzew już niekoniecznie binarnych (ale wciąż ukorzenionych)...
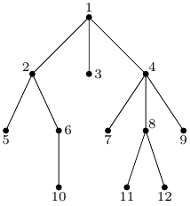
Rys. 1 Przykładowe drzewo ukorzenione o
 węzłach. Dla węzła o numerze 2 mamy
węzłach. Dla węzła o numerze 2 mamy
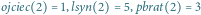 i
i
Przykład takiego drzewa można znaleźć na rysunku 1. Tym razem będziemy
nawigować po drzewie za pomocą operacji:
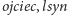 oraz
oraz
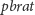 (ta ostatnia polega na przejściu do najbliższego po prawej brata danego węzła).
Aby operacja
(ta ostatnia polega na przejściu do najbliższego po prawej brata danego węzła).
Aby operacja
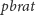 miała sens, musimy też umieć dla każdego węzła
wyznaczyć jego stopień, czyli liczbę synów (operacja
miała sens, musimy też umieć dla każdego węzła
wyznaczyć jego stopień, czyli liczbę synów (operacja
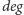 ). Spróbujmy
ustalić, jak oszczędną reprezentację mamy tu w ogóle szansę uzyskać. W tym
celu, podobnie jak w przypadku binarnym, musimy stwierdzić, ile jest
różnych drzew dowolnych o
). Spróbujmy
ustalić, jak oszczędną reprezentację mamy tu w ogóle szansę uzyskać. W tym
celu, podobnie jak w przypadku binarnym, musimy stwierdzić, ile jest
różnych drzew dowolnych o
 węzłach. Zliczać będziemy drzewa
z nienumerowanymi węzłami i w których porządek synów węzła ma
znaczenie. Niech
węzłach. Zliczać będziemy drzewa
z nienumerowanymi węzłami i w których porządek synów węzła ma
znaczenie. Niech
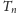 oznacza liczbę takich drzew (patrz Rys. 2). Jeśli
przez
oznacza liczbę takich drzew (patrz Rys. 2). Jeśli
przez
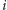 oznaczymy liczbę węzłów w poddrzewie skrajnie lewego syna
korzenia
oznaczymy liczbę węzłów w poddrzewie skrajnie lewego syna
korzenia
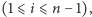 otrzymamy następujący wzór rekurencyjny na
otrzymamy następujący wzór rekurencyjny na
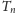 :
:

Mamy ponadto
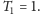 Porównując ten wzór z definicją rekurencyjną
liczb Catalana, otrzymujemy, że
Porównując ten wzór z definicją rekurencyjną
liczb Catalana, otrzymujemy, że
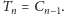 Stąd, podobnie jak
poprzednio, w oszczędnej reprezentacji drzew dowolnych powinno nam
wystarczyć
Stąd, podobnie jak
poprzednio, w oszczędnej reprezentacji drzew dowolnych powinno nam
wystarczyć
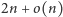 bitów.
bitów.
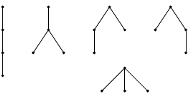
Rys. 2 Jest
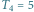 ukorzenionych, nieetykietowanych drzew o czterech węzłach.
ukorzenionych, nieetykietowanych drzew o czterech węzłach.
Przy konstrukcji ciągu kodowego znów ponumerujemy wszystkie węzły drzewa poziomami, a w ramach poziomów od lewej do prawej (Rys. 1). Wypiszmy teraz w jednym ciągu stopnie wszystkich węzłów – dla powyższego przykładu będzie to:

Chcielibyśmy, żeby taki właśnie ciąg był naszym ciągiem kodowym.
Niestety, nie jest to możliwe: występuje w nim
 liczb, z których
każda jest z zakresu od 0 do
liczb, z których
każda jest z zakresu od 0 do
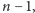 więc reprezentacja takiego ciągu
wymagałaby rzędu
więc reprezentacja takiego ciągu
wymagałaby rzędu
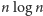 bitów. Aby sobie z tym poradzić,
zastosujemy pozornie beznadziejny manewr: zapiszemy wszystkie stopnie
unarnie, czyli każdy stopień zamienimy na ciąg jedynek odpowiedniej
długości zakończony zerem. Ponieważ suma stopni węzłów to zaledwie
bitów. Aby sobie z tym poradzić,
zastosujemy pozornie beznadziejny manewr: zapiszemy wszystkie stopnie
unarnie, czyli każdy stopień zamienimy na ciąg jedynek odpowiedniej
długości zakończony zerem. Ponieważ suma stopni węzłów to zaledwie
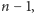 w ten sposób uzyskamy ciąg złożony z
w ten sposób uzyskamy ciąg złożony z
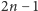 bitów,
np.:
bitów,
np.:

Ze względów technicznych wygodnie nam będzie jeszcze dodać do drzewa sztuczny korzeń, którego jedynym synem będzie faktyczny korzeń drzewa. Odpowiada to dopisaniu na początku ciągu jedynki i zera:

Taki ciąg kodowy o długości
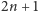 wraz ze strukturą danych do
wykonywania operacji rank/select będzie naszą bardzo oszczędną reprezentacją
drzewa.
wraz ze strukturą danych do
wykonywania operacji rank/select będzie naszą bardzo oszczędną reprezentacją
drzewa.
Spróbujmy uzasadnić, że podana reprezentacja umożliwia efektywne
wykonywanie wszystkich potrzebnych operacji. Zauważmy przede wszystkim,
że w ciągu kodowym występuje
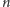 jedynek, które w naturalny sposób
odpowiadają węzłom drzewa: węzeł o numerze
jedynek, które w naturalny sposób
odpowiadają węzłom drzewa: węzeł o numerze
 reprezentuje
reprezentuje
 -ta
jedynka w ciągu, będąca zarazem odpowiednią jedynką w ciągu opisującym
stopień jego ojca. Każdemu węzłowi, oprócz już przydzielonego numeru
czarnego, przypiszemy znów numer kolorowy. Będzie to pozycja w ciągu
kodowym odpowiadającej mu jedynki. Widać natychmiast, że za pomocą
operacji rank oraz select możemy bez problemu przeliczać numery czarne na
kolorowe i odwrotnie.
-ta
jedynka w ciągu, będąca zarazem odpowiednią jedynką w ciągu opisującym
stopień jego ojca. Każdemu węzłowi, oprócz już przydzielonego numeru
czarnego, przypiszemy znów numer kolorowy. Będzie to pozycja w ciągu
kodowym odpowiadającej mu jedynki. Widać natychmiast, że za pomocą
operacji rank oraz select możemy bez problemu przeliczać numery czarne na
kolorowe i odwrotnie.
Wiedząc teraz, gdzie w ciągu kodowym znajduje się jedynka odpowiadająca
danemu węzłowi, możemy zliczyć zera występujące wcześniej w ciągu
i w ten sposób wyznaczyć numer jego ojca. Prawy brat węzła będzie ni
mniej, ni więcej jak sąsiednią jedynką w ciągu kodowym. Natomiast
ciąg jedynek odpowiadający synom węzła możemy zidentyfikować,
znajdując
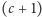 -sze i
-sze i
 -te zero w ciągu, gdzie
-te zero w ciągu, gdzie
 jest
numerem czarnym tego węzła. Z tego ciągu łatwo odzyskamy zarówno
numer lewego syna węzła, jak i łączną liczbę jego synów, czyli stopień
węzła.
jest
numerem czarnym tego węzła. Z tego ciągu łatwo odzyskamy zarówno
numer lewego syna węzła, jak i łączną liczbę jego synów, czyli stopień
węzła.
Dopracowanie szczegółów implementacji operacji pozostawiamy Czytelnikowi, który, wyposażony w strukturę danych rank/select, wykona to bez większego trudu.
Implementacja operacji rank i select. Przyszła pora, aby uzupełnić powyższe
rozważania opisem implementacji pomocniczej struktury danych. Zajmijmy się
najpierw operacją
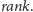 Zauważmy, że wystarczy umieć odpowiadać
na zapytania dla
Zauważmy, że wystarczy umieć odpowiadać
na zapytania dla
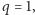 gdyż
gdyż
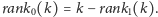
Nasz ciąg bitów
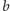 podzielimy na bloki: najpierw na duże bloki
o długości
podzielimy na bloki: najpierw na duże bloki
o długości
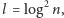 a w drugiej kolejności na małe bloki
o długości
a w drugiej kolejności na małe bloki
o długości
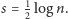 W zapisach tych
W zapisach tych
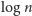 oznacza część
całkowitą logarytmu o podstawie dwójkowej z
oznacza część
całkowitą logarytmu o podstawie dwójkowej z
 Zakładamy dla
uproszczenia, że
Zakładamy dla
uproszczenia, że
 jest całkowite. Bloki w podziale są rozłączne
i składają się z kolejnych elementów ciągu. Ponadto, jeśli ostatni blok okaże
się krótszy, uzupełniamy go sztucznymi zerami aż do pełnej długości.
Zauważmy, że
jest całkowite. Bloki w podziale są rozłączne
i składają się z kolejnych elementów ciągu. Ponadto, jeśli ostatni blok okaże
się krótszy, uzupełniamy go sztucznymi zerami aż do pełnej długości.
Zauważmy, że
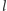 jest całkowitą wielokrotnością
jest całkowitą wielokrotnością
 i małe bloki
stanowią „podpodział” dużych bloków. Bloki każdego typu numerujemy od
jedynki.
i małe bloki
stanowią „podpodział” dużych bloków. Bloki każdego typu numerujemy od
jedynki.
Dla każdego dużego bloku w tablicy
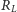 zapamiętamy łączną liczbę
jedynek w ciągu znajdujących się przed początkiem tego bloku. Elementy tablicy
zapamiętamy łączną liczbę
jedynek w ciągu znajdujących się przed początkiem tego bloku. Elementy tablicy
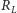 są mniejsze niż
są mniejsze niż
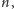 więc są liczbami złożonymi z co
najwyżej
więc są liczbami złożonymi z co
najwyżej
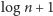 bitów. Łączny rozmiar tej tablicy jest zatem
rzędu:
bitów. Łączny rozmiar tej tablicy jest zatem
rzędu:

Dalej, dla każdego małego bloku w podobnej tablicy
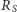 zapamiętamy
liczbę jedynek znajdujących się przed początkiem tego bloku, ale w ramach
dużego bloku zawierającego rozważany mały blok. Tablica
zapamiętamy
liczbę jedynek znajdujących się przed początkiem tego bloku, ale w ramach
dużego bloku zawierającego rozważany mały blok. Tablica
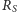 ma
ma
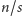 elementów, jednak każdy jej element jest mniejszy niż
elementów, jednak każdy jej element jest mniejszy niż
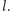 Tablica ma więc rozmiar rzędu:
Tablica ma więc rozmiar rzędu:

Obie tablice zajmują zatem
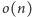 bitów.
bitów.
Łatwo dostrzec, w jaki sposób możemy użyć podanych tablic do odpowiedzi
na zapytanie
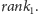 Widać też, że potrzebujemy do tego jeszcze jednej
informacji: o liczbie jedynek znajdujących się przed danym bitem w ramach jego
małego bloku. W tym miejscu wykorzystamy własność, że różnych co
do wartości małych bloków nie ma zbyt wiele. Dokładniej, jest tylko
Widać też, że potrzebujemy do tego jeszcze jednej
informacji: o liczbie jedynek znajdujących się przed danym bitem w ramach jego
małego bloku. W tym miejscu wykorzystamy własność, że różnych co
do wartości małych bloków nie ma zbyt wiele. Dokładniej, jest tylko
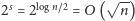 takich bloków i możemy je w naturalny
sposób ponumerować kolejnymi liczbami naturalnymi – numerem
bloku będzie liczba binarna zawarta w tym bloku. Teraz możemy dla
każdego z małych bloków wyznaczyć zawczasu wszystkie wyniki.
W tablicy
takich bloków i możemy je w naturalny
sposób ponumerować kolejnymi liczbami naturalnymi – numerem
bloku będzie liczba binarna zawarta w tym bloku. Teraz możemy dla
każdego z małych bloków wyznaczyć zawczasu wszystkie wyniki.
W tablicy
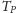 dla danego numeru małego bloku i dla każdego
indeksu w ramach małego bloku zapamiętamy liczbę jedynek na pozycjach
poprzedzających ten indeks (wraz z tym indeksem). Tablica ta będzie miała
dla danego numeru małego bloku i dla każdego
indeksu w ramach małego bloku zapamiętamy liczbę jedynek na pozycjach
poprzedzających ten indeks (wraz z tym indeksem). Tablica ta będzie miała
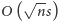 elementów, każdy nie większy niż
elementów, każdy nie większy niż
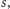 czyli jej łączny
rozmiar to:
czyli jej łączny
rozmiar to:

Ostatecznie wszystkie przechowywane tablice mają rozmiar
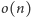 i pozwalają
odpowiedzieć na zapytanie
i pozwalają
odpowiedzieć na zapytanie
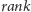 następująco:
następująco:
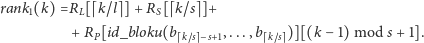 |
Odpowiedź na zapytanie uzyskujemy więc w czasie stałym, przy założeniu, że
standardowe operacje arytmetyczne i bitowe na liczbach nie większych
niż
 działają w czasie stałym. W tym celu wystarczy ciąg
działają w czasie stałym. W tym celu wystarczy ciąg
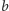 reprezentować w tablicy liczb całkowitych odpowiadających paczkom
kolejnych bitów ciągu (jeszcze łatwiej sobie wyobrazić, że w tablicy
pamiętamy po prostu kolejne identyfikatory małych bloków).
reprezentować w tablicy liczb całkowitych odpowiadających paczkom
kolejnych bitów ciągu (jeszcze łatwiej sobie wyobrazić, że w tablicy
pamiętamy po prostu kolejne identyfikatory małych bloków).
Z operacją
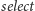 można poradzić sobie podobnie, jednak jest to dużo
bardziej skomplikowane technicznie. Tym razem bloki nie są stałej długości, lecz
wszystkie zawierają tę samą liczbę jedynek. Ponadto są tu potrzebne trzy
poziomy podziału na bloki – dokładny opis pomijamy. Natomiast Czytelnika
Zainteresowanego pozostawiamy z następującym pytaniem: dlaczego nie dało się
rozwiązać problemu zapytań
można poradzić sobie podobnie, jednak jest to dużo
bardziej skomplikowane technicznie. Tym razem bloki nie są stałej długości, lecz
wszystkie zawierają tę samą liczbę jedynek. Ponadto są tu potrzebne trzy
poziomy podziału na bloki – dokładny opis pomijamy. Natomiast Czytelnika
Zainteresowanego pozostawiamy z następującym pytaniem: dlaczego nie dało się
rozwiązać problemu zapytań
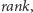 używając tylko jednego rozmiaru
bloków – powiedzmy,
używając tylko jednego rozmiaru
bloków – powiedzmy,
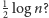
Citius, altius, fortius. W tym artykule opisaliśmy bardzo oszczędne reprezentacje drzew binarnych i dowolnych pozwalające efektywnie realizować podstawowe operacje związane z nawigacją po drzewie. Za pomocą bardziej zaawansowanych narzędzi zaprojektowano inne bardzo oszczędne reprezentacje drzew (bazujące na wyrażeniach nawiasowych równoważnych drzewom), które pozwalają wykonywać całe mnóstwo operacji: wyznaczanie rozmiarów poddrzew, wysokości i głębokości węzłów, znajdowanie najniższych wspólnych przodków (LCA) par węzłów i przodków węzłów na określonej głębokości, zliczanie liści w poddrzewach itd. Co więcej, z podanych tutaj pomysłów rozwinęła się cała dziedzina badań zajmująca się bardzo oszczędnymi strukturami danych. Więcej informacji na ten temat Czytelnik znajdzie w Internecie pod hasłem succinct data structures.
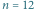 węzłach. Dla węzła o numerze 2 mamy
węzłach. Dla węzła o numerze 2 mamy
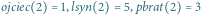 i
i
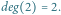
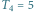 ukorzenionych, nieetykietowanych drzew o czterech węzłach.
ukorzenionych, nieetykietowanych drzew o czterech węzłach.