Bardzo oszczędne drzewa (I)
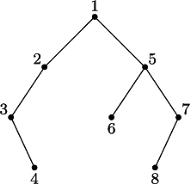
Rys. 1
Wiele struktur danych w komputerze można reprezentować w postaci drzewa binarnego. Aby przechować takie drzewo w pamięci komputera, należy dla każdego węzła zapamiętać numer jego lewego i prawego syna oraz, jeśli to potrzebne, numer węzła będącego jego ojcem. Wystarczą nam do tego trzy tablice.
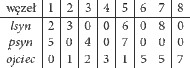
Rys. 2 Reprezentacja drzewa z rysunku 1 za pomocą trzech tablic lsyn, psyn i ojciec. Liczba 0 w tablicy oznacza, że odpowiedni węzeł drzewa nie istnieje.

Rys. 3 Jest
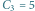 ukorzenionych, nieetykietowanych drzew binarnych o trzech węzłach.
ukorzenionych, nieetykietowanych drzew binarnych o trzech węzłach.
Czy jest to najbardziej oszczędna reprezentacja drzewa binarnego? Jeśli
rozważane drzewo ma
 węzłów, to łączny rozmiar wszystkich tablic
wynosi
węzłów, to łączny rozmiar wszystkich tablic
wynosi
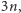 a jeśli nie są nam potrzebni ojcowie węzłów, to rozmiar
jest równy
a jeśli nie są nam potrzebni ojcowie węzłów, to rozmiar
jest równy
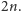 Co więcej, tablice lsyn i psyn mają łącznie tylko
Co więcej, tablice lsyn i psyn mają łącznie tylko
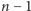 niezerowych komórek. Możemy przeanalizować to jeszcze
dokładniej i spojrzeć na liczbę bitów w reprezentacji. Numery węzłów są
u nas liczbami całkowitymi z zakresu od 1 do
niezerowych komórek. Możemy przeanalizować to jeszcze
dokładniej i spojrzeć na liczbę bitów w reprezentacji. Numery węzłów są
u nas liczbami całkowitymi z zakresu od 1 do
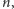 więc do reprezentacji
każdego z nich w systemie binarnym wystarczy
więc do reprezentacji
każdego z nich w systemie binarnym wystarczy
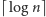 cyfr. To
oznacza, że cała reprezentacja wymaga z grubsza
cyfr. To
oznacza, że cała reprezentacja wymaga z grubsza
 bitów
pamięci, gdzie
bitów
pamięci, gdzie
 jest stałą równą 1, 2 lub 3, zależnie od tego,
które tablice przechowujemy. Kombinując dalej, można zauważyć, że
do przechowywania małych numerów węzłów nie jest potrzebne aż
jest stałą równą 1, 2 lub 3, zależnie od tego,
które tablice przechowujemy. Kombinując dalej, można zauważyć, że
do przechowywania małych numerów węzłów nie jest potrzebne aż
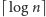 bitów, jednak to spostrzeżenie nie pozwoli nam na pewno
istotnie zredukować łącznej liczby bitów w reprezentacji.
bitów, jednak to spostrzeżenie nie pozwoli nam na pewno
istotnie zredukować łącznej liczby bitów w reprezentacji.
A czy jest możliwe uzyskanie reprezentacji drzewa binarnego za pomocą
istotnie mniej niż
 bitów? Aby odpowiedzieć na to pytanie,
warto zadać inne: ile jest różnych drzew binarnych (ukorzenionych,
nieetykietowanych) o
bitów? Aby odpowiedzieć na to pytanie,
warto zadać inne: ile jest różnych drzew binarnych (ukorzenionych,
nieetykietowanych) o
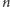 węzłach? Oznaczmy tę liczbę przez
węzłach? Oznaczmy tę liczbę przez
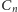 (patrz Rys. 3). Spróbujmy ułożyć wzór rekurencyjny na
(patrz Rys. 3). Spróbujmy ułożyć wzór rekurencyjny na
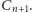 Drzewo o
Drzewo o
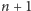 węzłach składa się z korzenia i dwóch jego
poddrzew. Oznaczmy przez
węzłach składa się z korzenia i dwóch jego
poddrzew. Oznaczmy przez
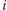 liczbę węzłów w lewym poddrzewie
liczbę węzłów w lewym poddrzewie
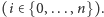 Wówczas:
Wówczas:
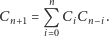 |
Dodając do tego wzoru warunek początkowy
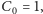 otrzymujemy
rekurencję definiującą tzw. liczby Catalana, o znanym wzorze ogólnym:
otrzymujemy
rekurencję definiującą tzw. liczby Catalana, o znanym wzorze ogólnym:
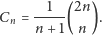 |
Znajomość wartości
 pozwala podać teoretyczne oszacowanie
dolne na liczbę bitów w reprezentacji drzewa binarnego o
pozwala podać teoretyczne oszacowanie
dolne na liczbę bitów w reprezentacji drzewa binarnego o
 węzłach.
Otóż żeby każde drzewo binarne dało się reprezentować za pomocą
węzłach.
Otóż żeby każde drzewo binarne dało się reprezentować za pomocą
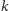 bitów, musi zachodzić
bitów, musi zachodzić
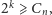 gdyż w przeciwnym razie
pewne dwa różne drzewa miałyby tę samą reprezentację. Ponieważ
współczynnik dwumianowy występujący we wzorze na
gdyż w przeciwnym razie
pewne dwa różne drzewa miałyby tę samą reprezentację. Ponieważ
współczynnik dwumianowy występujący we wzorze na
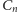 majoryzuje
pozostałe współczynniki występujące w sumie:
majoryzuje
pozostałe współczynniki występujące w sumie:
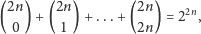 |
a
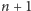 występujące w mianowniku jest niższego rzędu niż
występujące w mianowniku jest niższego rzędu niż
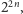 więc możemy z niezłą dokładnością asymptotyczną przybliżyć
więc możemy z niezłą dokładnością asymptotyczną przybliżyć
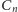 przez
przez


Stąd wysnuwamy wniosek, że do reprezentacji drzew binarnych powinno nam
wystarczyć mniej więcej
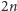 bitów. Oczywiście, taka reprezentacja
istnieje. Wystarczy wszystkie
bitów. Oczywiście, taka reprezentacja
istnieje. Wystarczy wszystkie
 -węzłowe drzewa binarne ponumerować
kolejnymi liczbami naturalnymi. Wówczas reprezentacją danego drzewa będzie
jego numer, czyli liczba naturalna o co najwyżej
-węzłowe drzewa binarne ponumerować
kolejnymi liczbami naturalnymi. Wówczas reprezentacją danego drzewa będzie
jego numer, czyli liczba naturalna o co najwyżej
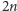 bitach. Taka
reprezentacja, jakkolwiek niezwykle oszczędna, jest, niestety, dużo mniej wygodna
niż nasza początkowa reprezentacja wykorzystująca
bitach. Taka
reprezentacja, jakkolwiek niezwykle oszczędna, jest, niestety, dużo mniej wygodna
niż nasza początkowa reprezentacja wykorzystująca
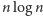 bitów.
Nie pozwala ona nawigować po drzewie, tj. identyfikować węzłów
drzewa i poruszać się po nich w naturalny sposób, czyli w kierunku do
synów lub do ojca węzła. Okazuje się jednak, że istnieje inna, sprytna
reprezentacja drzew binarnych, która wykorzystuje mniej więcej tyle
samo bitów – dokładniej
bitów.
Nie pozwala ona nawigować po drzewie, tj. identyfikować węzłów
drzewa i poruszać się po nich w naturalny sposób, czyli w kierunku do
synów lub do ojca węzła. Okazuje się jednak, że istnieje inna, sprytna
reprezentacja drzew binarnych, która wykorzystuje mniej więcej tyle
samo bitów – dokładniej
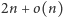 bitów, czyli więcej tylko
o składnik niższego rzędu – i umożliwia łatwą nawigację po drzewie.
W dalszej części artykułu przedstawimy taką właśnie bardzo oszczędną
reprezentację.
bitów, czyli więcej tylko
o składnik niższego rzędu – i umożliwia łatwą nawigację po drzewie.
W dalszej części artykułu przedstawimy taką właśnie bardzo oszczędną
reprezentację.
Rank i select Na początek wprowadzimy pomocniczą strukturę danych
operującą na ciągach binarnych. Chcielibyśmy umieć obsługiwać dwa typy
zapytań dotyczące takich ciągów: wyznaczanie
 -tej jedynki
(względnie
-tej jedynki
(względnie
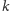 -tego zera) w ciągu – operacja
-tego zera) w ciągu – operacja
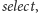 oraz
sprawdzanie, ile jedynek (względnie ile zer) znajduje się w ciągu do ustalonej
pozycji – operacja
oraz
sprawdzanie, ile jedynek (względnie ile zer) znajduje się w ciągu do ustalonej
pozycji – operacja
 Formalnie, niech
Formalnie, niech
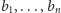 będzie
ustalonym ciągiem zero-jedynkowym. Wówczas dla
będzie
ustalonym ciągiem zero-jedynkowym. Wówczas dla
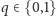 oraz
oraz
 zapytania mają postać:
zapytania mają postać:

Okazuje się, że istnieje struktura danych, która poza ciągiem
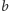 zużywa
zużywa
 bitów pamięci i pozwala odpowiadać na
określone tu zapytania w czasie stałym. Odtąd będziemy używać tej struktury
danych jako czarnej skrzynki (ang. black box).
bitów pamięci i pozwala odpowiadać na
określone tu zapytania w czasie stałym. Odtąd będziemy używać tej struktury
danych jako czarnej skrzynki (ang. black box).
Bardzo oszczędna reprezentacja drzew. Użyjemy teraz naszej pomocniczej struktury danych do konstrukcji bardzo oszczędnej reprezentacji drzew binarnych. Zacznijmy od uzupełnienia drzewa binarnego tzw. węzłami zewnętrznymi, tak aby każdy węzeł wewnętrzny miał dokładnie dwóch synów (Rys. 4). Węzły wewnętrzne drzewa ponumerujmy poziomami, a w ramach poziomów od lewej do prawej (czarne numery na rysunku 4). Ponadto w ten sam sposób ponumerujmy wszystkie węzły drzewa (kolorowe numery na rysunku 4).
Obejdźmy teraz wszystkie węzły drzewa w porządku numerów „kolorowych” i dla każdego z nich zapiszmy cyfrę 1, jeśli jest on węzłem wewnętrznym, a 0 w przeciwnym przypadku:
 |
Tak otrzymany ciąg binarny wraz z powiązaną z nim strukturą danych do
wykonywania operacji rank/select będzie stanowił bardzo oszczędną
reprezentację drzewa, tzw. ciąg kodowy. Każdy węzeł uzupełnionego drzewa
poza korzeniem jest synem jednego z
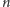 węzłów wewnętrznych. Stąd
łączna liczba węzłów drzewa, a zarazem liczba bitów w ciągu kodowym to
węzłów wewnętrznych. Stąd
łączna liczba węzłów drzewa, a zarazem liczba bitów w ciągu kodowym to

Sprawdźmy teraz, na ile użyteczny jest nasz ciąg kodowy. Każdy węzeł
wewnętrzny drzewa
 ma dwa numery, czarny
ma dwa numery, czarny
 i kolorowy
i kolorowy
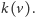 Aby przeliczyć numer czarny na kolorowy, wystarczy znaleźć
Aby przeliczyć numer czarny na kolorowy, wystarczy znaleźć
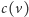 -tą jedynkę w ciągu kodowym, czyli wykonać operację
-tą jedynkę w ciągu kodowym, czyli wykonać operację
 :
:
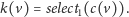 |
Przyporządkowanie odwrotne wykonujemy za pomocą operacji
 :
:
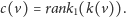 |
Musimy jeszcze opisać sposób poruszania się po drzewie. Jest on zaskakująco prosty:
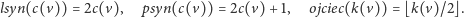 |
Innymi słowy, lewym synem węzła o numerze czarnym
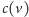 jest
węzeł o numerze kolorowym
jest
węzeł o numerze kolorowym
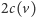 i podobnie w przypadku
prawego syna; natomiast w przypadku ojca robimy odwrotnie: dla węzła
o numerze kolorowym
i podobnie w przypadku
prawego syna; natomiast w przypadku ojca robimy odwrotnie: dla węzła
o numerze kolorowym
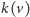 ojcem jest węzeł o numerze czarnym
ojcem jest węzeł o numerze czarnym
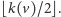
Podane wzory zasługują na wyjaśnienie. Skoncentrujemy się na pierwszym
z nich (dla operacji
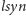 ), pozostałe otrzymuje się analogicznie. Aby
go uzasadnić, wystarczy zbadać, ile węzłów uzupełnionego drzewa
występuje w porządku kolejnych poziomów przed lewym synem węzła
), pozostałe otrzymuje się analogicznie. Aby
go uzasadnić, wystarczy zbadać, ile węzłów uzupełnionego drzewa
występuje w porządku kolejnych poziomów przed lewym synem węzła
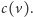 Każdy taki węzeł jest albo samym korzeniem drzewa,
albo synem jednego z węzłów wewnętrznych o czarnych numerach
Każdy taki węzeł jest albo samym korzeniem drzewa,
albo synem jednego z węzłów wewnętrznych o czarnych numerach
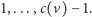 Zauważmy, że do tej drugiej grupy zaliczają się tak
węzły wewnętrzne (w tym te o numerach czarnych
Zauważmy, że do tej drugiej grupy zaliczają się tak
węzły wewnętrzne (w tym te o numerach czarnych
 ),
jak i zewnętrzne. Wszystkich tych węzłów jest
),
jak i zewnętrzne. Wszystkich tych węzłów jest
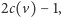 więc
rzeczywiście numerem kolorowym lewego syna węzła
więc
rzeczywiście numerem kolorowym lewego syna węzła
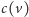 jest
jest
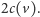
Podsumujmy to, co wiemy o naszej reprezentacji. Ma ona rozmiar
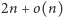 i pozwala identyfikować węzły drzewa i przemieszczać się
w górę i w dół drzewa w czasie stałym. Nie wykazaliśmy jeszcze tylko, że
jest ona poprawna, czyli że różne drzewa uzyskują różne reprezentacje. To
jednakże wynika z faktu, że na podstawie reprezentacji drzewa, nawigując po
nim, możemy jednoznacznie odtworzyć jego kształt. Tak więc nasza
reprezentacja spełnia wszystkie oczekiwane własności.
i pozwala identyfikować węzły drzewa i przemieszczać się
w górę i w dół drzewa w czasie stałym. Nie wykazaliśmy jeszcze tylko, że
jest ona poprawna, czyli że różne drzewa uzyskują różne reprezentacje. To
jednakże wynika z faktu, że na podstawie reprezentacji drzewa, nawigując po
nim, możemy jednoznacznie odtworzyć jego kształt. Tak więc nasza
reprezentacja spełnia wszystkie oczekiwane własności.
Rank i select
Rank i select Na początek wprowadzimy pomocniczą strukturę danych
operującą na ciągach binarnych. Chcielibyśmy umieć obsługiwać dwa typy
zapytań dotyczące takich ciągów: wyznaczanie
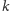 -tej jedynki
(względnie
-tej jedynki
(względnie
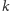 -tego zera) w ciągu – operacja
-tego zera) w ciągu – operacja
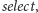 oraz
sprawdzanie, ile jedynek (względnie ile zer) znajduje się w ciągu do ustalonej
pozycji – operacja
oraz
sprawdzanie, ile jedynek (względnie ile zer) znajduje się w ciągu do ustalonej
pozycji – operacja
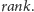 Formalnie, niech
Formalnie, niech
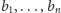 będzie
ustalonym ciągiem zero-jedynkowym. Wówczas dla
będzie
ustalonym ciągiem zero-jedynkowym. Wówczas dla
 oraz
oraz
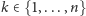 zapytania mają postać:
zapytania mają postać:

Okazuje się, że istnieje struktura danych, która poza ciągiem
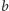 zużywa
zużywa
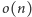 bitów pamięci i pozwala odpowiadać na
określone tu zapytania w czasie stałym. Odtąd będziemy używać tej struktury
danych jako czarnej skrzynki (ang. black box).
bitów pamięci i pozwala odpowiadać na
określone tu zapytania w czasie stałym. Odtąd będziemy używać tej struktury
danych jako czarnej skrzynki (ang. black box).
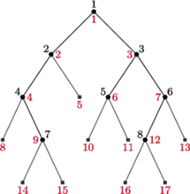
Rys. 4 Uzupełnienie drzewa binarnego z Rys. 1 węzłami zewnętrznymi.
Bardzo oszczędna reprezentacja drzew
Użyjemy teraz naszej pomocniczej struktury danych do konstrukcji bardzo oszczędnej reprezentacji drzew binarnych. Zacznijmy od uzupełnienia drzewa binarnego tzw. węzłami zewnętrznymi, tak aby każdy węzeł wewnętrzny miał dokładnie dwóch synów (Rys. 4). Węzły wewnętrzne drzewa ponumerujmy poziomami, a w ramach poziomów od lewej do prawej (czarne numery na rysunku 4). Ponadto w ten sam sposób ponumerujmy wszystkie węzły drzewa (kolorowe numery na rysunku 4).
Obejdźmy teraz wszystkie węzły drzewa w porządku numerów „kolorowych” i dla każdego z nich zapiszmy cyfrę 1, jeśli jest on węzłem wewnętrznym, a 0 w przeciwnym przypadku:
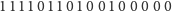 |
Tak otrzymany ciąg binarny wraz z powiązaną z nim strukturą danych do
wykonywania operacji rank/select będzie stanowił bardzo oszczędną
reprezentację drzewa, tzw. ciąg kodowy. Każdy węzeł uzupełnionego drzewa
poza korzeniem jest synem jednego z
 węzłów wewnętrznych. Stąd
łączna liczba węzłów drzewa, a zarazem liczba bitów w ciągu kodowym to
węzłów wewnętrznych. Stąd
łączna liczba węzłów drzewa, a zarazem liczba bitów w ciągu kodowym to
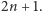
Sprawdźmy teraz, na ile użyteczny jest nasz ciąg kodowy. Każdy węzeł
wewnętrzny drzewa
 ma dwa numery, czarny
ma dwa numery, czarny
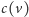 i kolorowy
i kolorowy
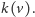 Aby przeliczyć numer czarny na kolorowy, wystarczy znaleźć
Aby przeliczyć numer czarny na kolorowy, wystarczy znaleźć
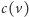 -tą jedynkę w ciągu kodowym, czyli wykonać operację
-tą jedynkę w ciągu kodowym, czyli wykonać operację
 :
:
 |
Przyporządkowanie odwrotne wykonujemy za pomocą operacji
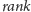 :
:
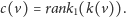 |
Musimy jeszcze opisać sposób poruszania się po drzewie. Jest on zaskakująco prosty:
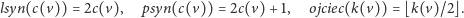 |
Innymi słowy, lewym synem węzła o numerze czarnym
 jest
węzeł o numerze kolorowym
jest
węzeł o numerze kolorowym
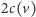 i podobnie w przypadku
prawego syna; natomiast w przypadku ojca robimy odwrotnie: dla węzła
o numerze kolorowym
i podobnie w przypadku
prawego syna; natomiast w przypadku ojca robimy odwrotnie: dla węzła
o numerze kolorowym
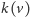 ojcem jest węzeł o numerze czarnym
ojcem jest węzeł o numerze czarnym
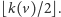
Podane wzory zasługują na wyjaśnienie. Skoncentrujemy się na pierwszym
z nich (dla operacji
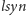 ), pozostałe otrzymuje się analogicznie. Aby
go uzasadnić, wystarczy zbadać, ile węzłów uzupełnionego drzewa
występuje w porządku kolejnych poziomów przed lewym synem węzła
), pozostałe otrzymuje się analogicznie. Aby
go uzasadnić, wystarczy zbadać, ile węzłów uzupełnionego drzewa
występuje w porządku kolejnych poziomów przed lewym synem węzła
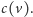 Każdy taki węzeł jest albo samym korzeniem drzewa,
albo synem jednego z węzłów wewnętrznych o czarnych numerach
Każdy taki węzeł jest albo samym korzeniem drzewa,
albo synem jednego z węzłów wewnętrznych o czarnych numerach
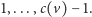 Zauważmy, że do tej drugiej grupy zaliczają się tak
węzły wewnętrzne (w tym te o numerach czarnych
Zauważmy, że do tej drugiej grupy zaliczają się tak
węzły wewnętrzne (w tym te o numerach czarnych
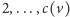 ),
jak i zewnętrzne. Wszystkich tych węzłów jest
),
jak i zewnętrzne. Wszystkich tych węzłów jest
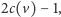 więc
rzeczywiście numerem kolorowym lewego syna węzła
więc
rzeczywiście numerem kolorowym lewego syna węzła
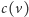 jest
jest
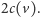
Podsumujmy to, co wiemy o naszej reprezentacji. Ma ona rozmiar
 i pozwala identyfikować węzły drzewa i przemieszczać się
w górę i w dół drzewa w czasie stałym. Nie wykazaliśmy jeszcze tylko, że
jest ona poprawna, czyli że różne drzewa uzyskują różne reprezentacje. To
jednakże wynika z faktu, że na podstawie reprezentacji drzewa, nawigując po
nim, możemy jednoznacznie odtworzyć jego kształt. Tak więc nasza
reprezentacja spełnia wszystkie oczekiwane własności.
i pozwala identyfikować węzły drzewa i przemieszczać się
w górę i w dół drzewa w czasie stałym. Nie wykazaliśmy jeszcze tylko, że
jest ona poprawna, czyli że różne drzewa uzyskują różne reprezentacje. To
jednakże wynika z faktu, że na podstawie reprezentacji drzewa, nawigując po
nim, możemy jednoznacznie odtworzyć jego kształt. Tak więc nasza
reprezentacja spełnia wszystkie oczekiwane własności.
 ukorzenionych, nieetykietowanych drzew binarnych o trzech węzłach.
ukorzenionych, nieetykietowanych drzew binarnych o trzech węzłach.