Informatyczny kącik olimpijski
Dwa zadania z Potyczek
W tym kąciku omówimy dwa zadania z Potyczek Algorytmicznych 2012. Pomimo krótkich rozwiązań, zadania te wymagały od zawodników niemałej dozy pomysłowości.
Treść zadania Korniki wygodnie nam będzie streścić w terminologii numizmatycznej:
Zadanie 1 (Kornik). na stole w jednym rzędzie leży
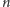 monet o nominałach
monet o nominałach
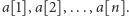 Dwóch graczy
na przemian wykonuje ruchy. Ruch polega na zabraniu monety z lewego
końca, z prawego końca lub z obu końców rzędu naraz. Wiedząc, że
każdy z graczy gra tak, by zmaksymalizować sumę wartości zabranych
przez siebie monet, należy wyznaczyć wynik gry (różnicę między zyskiem
pierwszego i drugiego gracza).
Dwóch graczy
na przemian wykonuje ruchy. Ruch polega na zabraniu monety z lewego
końca, z prawego końca lub z obu końców rzędu naraz. Wiedząc, że
każdy z graczy gra tak, by zmaksymalizować sumę wartości zabranych
przez siebie monet, należy wyznaczyć wynik gry (różnicę między zyskiem
pierwszego i drugiego gracza).
Symulując wprost reguły gry, dostajemy algorytm działający w czasie
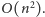 Wypełniamy kwadratową tablicę, gdzie
Wypełniamy kwadratową tablicę, gdzie
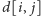 oznacza
wynik gry dla ciągu monet na pozycjach o numerach
oznacza
wynik gry dla ciągu monet na pozycjach o numerach
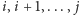 (zatem
(zatem
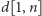 jest odpowiedzią do zadania). Jeśli pominiemy warunki
brzegowe, rekurencja będzie następująca:
jest odpowiedzią do zadania). Jeśli pominiemy warunki
brzegowe, rekurencja będzie następująca:
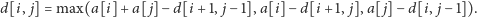 | (*) |
Istnieje jednak efektywniejsze rozwiązanie. Załóżmy najpierw, że
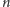 jest
nieparzyste. Oznaczmy sumę nominałów monet na pozycjach nieparzystych
oraz parzystych przez
jest
nieparzyste. Oznaczmy sumę nominałów monet na pozycjach nieparzystych
oraz parzystych przez
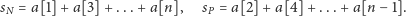 |
Zauważmy, że pierwszy gracz ma strategię, która pozwala mu na zabranie
wszystkich monet na pozycjach nieparzystych (niezależnie od ruchów drugiego
gracza – w swoim pierwszym ruchu zabiera dwie monety, a w każdym
kolejnym ruchu kopiuje ostatni ruch drugiego gracza). Gwarantuje mu to
uzyskanie wyniku nie mniejszego niż
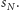 Z kolei gracz drugi ma
strategię, która pozwala mu na zabranie wszystkich monet na pozycjach
parzystych (również kopiuje ruchy przeciwnika), co gwarantuje mu uzyskanie
wyniku nie mniejszego niż
Z kolei gracz drugi ma
strategię, która pozwala mu na zabranie wszystkich monet na pozycjach
parzystych (również kopiuje ruchy przeciwnika), co gwarantuje mu uzyskanie
wyniku nie mniejszego niż
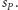 Zatem obaj gracze uzyskają właśnie tyle,
a wynikiem gry będzie
Zatem obaj gracze uzyskają właśnie tyle,
a wynikiem gry będzie


Dla
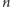 parzystego nie widać, jak to zrobić równie prosto. Zatem pozostaje
nam skorzystać ze wzoru
parzystego nie widać, jak to zrobić równie prosto. Zatem pozostaje
nam skorzystać ze wzoru
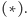 Ograniczymy się jednak do wyznaczenia
wartości
Ograniczymy się jednak do wyznaczenia
wartości
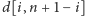 dla
dla
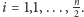 Zauważmy, że przy
obliczaniu każdej z nich pierwszy wyraz pod maksimum jest również
tej postaci, natomiast dwa pozostałe dotyczą fragmentów długości
nieparzystej, z którymi umiemy już sobie łatwo radzić. Rzeczywiście,
jeśli stablicujemy sumy prefiksowe ciągu z naprzemiennym znakiem,
możemy obliczyć wartość gry dla dowolnego takiego fragmentu w czasie
stałym. Ostatecznie otrzymujemy rozwiązanie o złożoności czasowej
Zauważmy, że przy
obliczaniu każdej z nich pierwszy wyraz pod maksimum jest również
tej postaci, natomiast dwa pozostałe dotyczą fragmentów długości
nieparzystej, z którymi umiemy już sobie łatwo radzić. Rzeczywiście,
jeśli stablicujemy sumy prefiksowe ciągu z naprzemiennym znakiem,
możemy obliczyć wartość gry dla dowolnego takiego fragmentu w czasie
stałym. Ostatecznie otrzymujemy rozwiązanie o złożoności czasowej
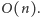
Zadanie 2 (Podatek). Dany jest graf nieskierowany
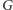 reprezentujący sieć
dróg pomiędzy miastami. Każda droga ma przypisaną stawkę podatku. Jadąc
z miasta do miasta, musimy w każdym mieście pośrednim uiścić opłatę
równą maksimum ze stawki podatku dla drogi, którą wjechaliśmy do
miasta, i dla drogi, którą z miasta wyjedziemy. Dla miasta pierwszego
i ostatniego rozważamy tylko jedną stawkę. Przykładowo, jadąc trasą
reprezentujący sieć
dróg pomiędzy miastami. Każda droga ma przypisaną stawkę podatku. Jadąc
z miasta do miasta, musimy w każdym mieście pośrednim uiścić opłatę
równą maksimum ze stawki podatku dla drogi, którą wjechaliśmy do
miasta, i dla drogi, którą z miasta wyjedziemy. Dla miasta pierwszego
i ostatniego rozważamy tylko jedną stawkę. Przykładowo, jadąc trasą
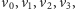 jeśli przez
jeśli przez
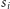 oznaczymy stawkę podatku na drodze
pomiędzy
oznaczymy stawkę podatku na drodze
pomiędzy
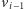 a
a
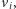 zapłacimy
zapłacimy
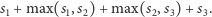 |
Należy podać minimalną opłatę przejazdu pomiędzy dwoma ustalonymi miastami.
Skorzystamy ze wzoru
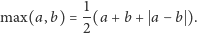 |
Możemy wtedy zapisać dwukrotność opłaty, którą uiścimy w naszym przykładzie, jako
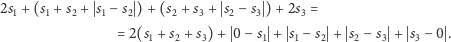 |
 Dla każdego wierzchołka
Dla każdego wierzchołka
 z grafu
z grafu
 do którego wchodzą krawędzie o wagach
do którego wchodzą krawędzie o wagach
 tworzymy w grafie
tworzymy w grafie
 wierzchołki
wierzchołki


 oraz łączymy
oraz łączymy
 i
i
 krawędzią o wadze
krawędzią o wadze
 Ponadto, dla
każdej krawędzi o wadze
Ponadto, dla
każdej krawędzi o wadze
 łączącej w
łączącej w
 wierzchołki
wierzchołki
 i
i
 dodajemy w
dodajemy w
 krawędź o wadze
krawędź o wadze
 pomiędzy
wierzchołkami
pomiędzy
wierzchołkami
 i
i

Pozostaje zauważyć istnienie bijekcji pomiędzy ścieżkami z
 do
do
 w grafie
w grafie
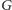 a ścieżkami z
a ścieżkami z
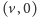 do
do
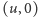 w grafie
w grafie
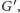 w której dwukrotność opłaty za ścieżkę w
w której dwukrotność opłaty za ścieżkę w
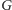 jest
równa zwykłej wadze ścieżki w
jest
równa zwykłej wadze ścieżki w
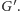 Graf
Graf
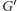 ma
ma
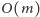 wierzchołków i
wierzchołków i
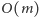 krawędzi, więc uruchomienie na
nim algorytmu Dijkstry zajmie czas
krawędzi, więc uruchomienie na
nim algorytmu Dijkstry zajmie czas