Na granicy możliwości
Algorytm to sposób rozwiązania pewnego problemu. Informatyka i matematyka od dawna badają różnego rodzaju problemy, szukając dla nich algorytmów, najczęściej możliwie szybkich. My jednak tym razem postąpimy wręcz przeciwnie: zajmiemy się algorytmami wyjątkowo wolnymi.
Najpierw wypada powiedzieć, że istnieją problemy, dla których w ogóle nie istnieje algorytm, który je rozwiązuje. Nie tylko nie znamy ani jednego, ale nawet potrafimy udowodnić, że żadnego nie ma. Takie problemy nazywa się nierozstrzygalnymi; najsławniejszy to problem stopu. Formułuje się go tak: dany jest pewien algorytm i należy stwierdzić, czy program, który będzie go realizował, kiedyś się zatrzyma. Nierozstrzygalność tego problemu oznacza więc, że nie istnieje żaden ogólny sposób, żeby stwierdzić, czy program, któremu właśnie się przyglądamy, zatrzyma się w pewnym momencie czy też będzie pracował w nieskończoność.
Tym razem zajmiemy się jednak metodą konstruowania algorytmów
dla problemów, które co prawda można rozwiązać, ale nie istnieje
dla nich żaden algorytm działający w jakimkolwiek rozsądnym czasie.
O takich problemach mówimy, że nie są pierwotnie rekurencyjne. Można
śmiało stwierdzić, że są one prawie nierozstrzygalne – na granicy
możliwości rozwiązania. Żeby lepiej wyobrazić sobie, jak dziwne muszą być
takie zagadnienia, sprecyzujmy, co rozumiemy przez problem, który
nie jest pierwotnie rekurencyjny. Powiedzmy, że dane wejściowe są
wielkości
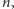 jeśli mają
jeśli mają
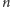 bitów – w tym sensie, na przykład,
liczba
bitów – w tym sensie, na przykład,
liczba

da się zapisać na 11 bitach, czyli ma wielkość 11.
Zdefiniujmy teraz funkcje
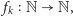 gdzie
gdzie
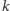 przebiega zbiór
liczb naturalnych. Przyjmujemy
przebiega zbiór
liczb naturalnych. Przyjmujemy
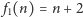 oraz
oraz

dla
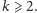 Czyli
Czyli
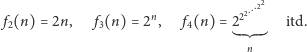
Można sobie tylko próbować wyobrazić, co dzieje się dalej. Funkcje, dla
których istnieje oszacowanie z góry przez pewną funkcję
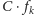 (dla
(dla
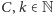 ), nazywamy funkcjami pierwotnie rekurencyjnymi. Zatem
funkcje, które nie są pierwotnie rekurencyjne, to takie, które rosną jeszcze
szybciej niż funkcje
), nazywamy funkcjami pierwotnie rekurencyjnymi. Zatem
funkcje, które nie są pierwotnie rekurencyjne, to takie, które rosną jeszcze
szybciej niż funkcje
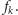 Przykład funkcji, która nie jest pierwotnie
rekurencyjna, to funkcja
Przykład funkcji, która nie jest pierwotnie
rekurencyjna, to funkcja
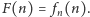 Czytelnik Wnikliwy może się
przekonać, że istotnie dla każdej funkcji
Czytelnik Wnikliwy może się
przekonać, że istotnie dla każdej funkcji
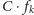 istnieje takie
istnieje takie
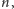 że
że
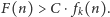 Podobnie definiuje się inny znany
przykład: funkcję Ackermanna.
Podobnie definiuje się inny znany
przykład: funkcję Ackermanna.
Powiemy też, że problem nie jest pierwotnie rekurencyjny, jeśli nie istnieje
żaden algorytm dla tego problemu, który dla każdych danych wielkości
 wykonuje co najwyżej
wykonuje co najwyżej
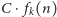 operacji dla pewnych
operacji dla pewnych
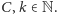 O dziwo, znamy jednak techniki, które pozwalają nam
projektować algorytmy działające w czasie nieograniczonym przez funkcję
pierwotnie rekurencyjną. Najpierw przedstawmy jednak głównego bohatera,
czyli badany problem.
O dziwo, znamy jednak techniki, które pozwalają nam
projektować algorytmy działające w czasie nieograniczonym przez funkcję
pierwotnie rekurencyjną. Najpierw przedstawmy jednak głównego bohatera,
czyli badany problem.
Będziemy rozważać wektory składające się z
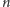 liczb naturalnych, czyli
elementy zbioru
liczb naturalnych, czyli
elementy zbioru
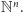 Dany jest wektor początkowy
Dany jest wektor początkowy
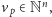 wektor
końcowy
wektor
końcowy
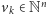 oraz skończony zbiór wektorów krokowych
oraz skończony zbiór wektorów krokowych
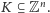 Zwróćmy uwagę na to, że w wektorach krokowych
dopuszczamy ujemne współrzędne! Pytanie brzmi: czy możemy w skończonej
liczbie ruchów dojść z punktu
Zwróćmy uwagę na to, że w wektorach krokowych
dopuszczamy ujemne współrzędne! Pytanie brzmi: czy możemy w skończonej
liczbie ruchów dojść z punktu
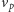 do punktu
do punktu
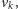 o ile mamy do
dyspozycji następujące ruchy:
o ile mamy do
dyspozycji następujące ruchy:
- 1.
- dodanie wektora krokowego, o ile to nie spowoduje, że wyjdziemy poza
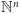 :
:
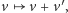 gdzie
gdzie
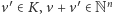 ;
;
- 2.
- zmniejszenie którejś
współrzędnej, o ile to nie spowoduje, że wyjdziemy poza
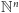 :
:
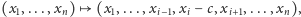 gdzie
gdzie
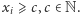
Jeśli istnieje takie przejście, to nazwiemy je ścieżką z
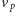 do
do
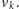
Dla powyższego problemu można podać algorytm działający w czasie rzędu
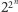 (czyli ten problem jest pierwotnie rekurencyjny). Ale właśnie ten
przykład świetnie ilustruje techniki, za pomocą których rozwiązuje się
nawet dużo trudniejsze problemy, w tym takie, które nie są pierwotnie
rekurencyjne.
(czyli ten problem jest pierwotnie rekurencyjny). Ale właśnie ten
przykład świetnie ilustruje techniki, za pomocą których rozwiązuje się
nawet dużo trudniejsze problemy, w tym takie, które nie są pierwotnie
rekurencyjne.
Na początek przedstawimy nasze główne narzędzie: lemat Dicksona. Powiemy,
że wektor
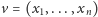 jest mniejszy lub równy niż wektor
jest mniejszy lub równy niż wektor
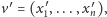 jeśli
jeśli
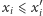 dla każdej współrzędnej
dla każdej współrzędnej
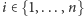 ; piszemy wtedy
; piszemy wtedy
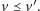
Lemat 1 (Dicksona). Niech
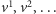 będzie nieskończonym ciągiem
wektorów z
będzie nieskończonym ciągiem
wektorów z
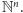 Wówczas istnieją pewne dwa indeksy
Wówczas istnieją pewne dwa indeksy
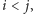 takie, że
takie, że
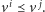
Algorytm sprawdzający, czy istnieje ścieżka z
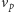 do
do
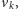 składa
się z dwóch procedur działających równocześnie (lub – jak kto woli –
wykonujących kroki na zmianę). Pierwsza – nazwijmy ją pozytywną – usiłuje
znaleźć ścieżkę z
składa
się z dwóch procedur działających równocześnie (lub – jak kto woli –
wykonujących kroki na zmianę). Pierwsza – nazwijmy ją pozytywną – usiłuje
znaleźć ścieżkę z
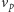 do
do
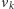 (czyli konstruktywny dowód
na to, że taka istnieje), druga natomiast – nazwijmy ją negatywną –
próbuje znaleźć dowód, że nie ma żadnej ścieżki z
(czyli konstruktywny dowód
na to, że taka istnieje), druga natomiast – nazwijmy ją negatywną –
próbuje znaleźć dowód, że nie ma żadnej ścieżki z
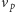 do
do
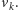 Istotne jest, żebyśmy dobrze zaprojektowali obie procedury: jeśli
szukana ścieżka istnieje, to procedura pozytywna musi w pewnym momencie
ją znaleźć, a jeśli ścieżka nie istnieje, to procedura negatywna ma
w pewnym momencie otrzymać dowód tego faktu. Wówczas w każdym
przypadku jedna z procedur się zatrzyma i nasz algorytm zakończy się,
zwracając właściwą odpowiedź. Zauważmy, że a priori nie mamy żadnego
oszacowania na to, kiedy program zakończy działanie, i dla niektórych
problemów rzeczywiście oczekiwanie na ten moment będzie trwać bardzo
długo.
Istotne jest, żebyśmy dobrze zaprojektowali obie procedury: jeśli
szukana ścieżka istnieje, to procedura pozytywna musi w pewnym momencie
ją znaleźć, a jeśli ścieżka nie istnieje, to procedura negatywna ma
w pewnym momencie otrzymać dowód tego faktu. Wówczas w każdym
przypadku jedna z procedur się zatrzyma i nasz algorytm zakończy się,
zwracając właściwą odpowiedź. Zauważmy, że a priori nie mamy żadnego
oszacowania na to, kiedy program zakończy działanie, i dla niektórych
problemów rzeczywiście oczekiwanie na ten moment będzie trwać bardzo
długo.
Zaprojektowanie procedury pozytywnej jest łatwe. Po prostu sprawdzane są
wszystkie możliwe ciągi ruchów, zaczynając od najkrótszych, a potem
przegląda się coraz dłuższe. Dla każdego z nich testujemy, czy może
przypadkiem prowadzi on z
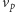 do
do
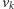 i nie powoduje nigdzie po
drodze zejścia poniżej zera.
i nie powoduje nigdzie po
drodze zejścia poniżej zera.
Problem leży w konstrukcji procedury negatywnej. Jak w ogóle może
wyglądać dowód nieistnienia ścieżki między danymi punktami? Rozważmy
zbiór
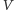 wszystkich takich wektorów
wszystkich takich wektorów
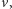 że istnieje z nich
ścieżka do wektora końcowego
że istnieje z nich
ścieżka do wektora końcowego
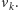 Zauważmy, że zbiór
Zauważmy, że zbiór
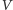 jest zamknięty w górę: jeśli
jest zamknięty w górę: jeśli
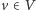 oraz
oraz
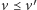 dla
pewnego wektora
dla
pewnego wektora
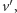 to również
to również
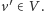 Istotnie, możemy
bowiem z
Istotnie, możemy
bowiem z
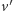 łatwo dojść do
łatwo dojść do
 (zmniejszając niektóre
współrzędne), a stąd do
(zmniejszając niektóre
współrzędne), a stąd do
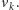 Jeżeli z
Jeżeli z
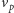 nie da się dojść do
nie da się dojść do
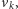 to zbiór
to zbiór
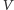 spełnia następujące warunki:
spełnia następujące warunki:
-
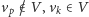 ;
;
-
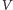 jest zamknięty w górę;
jest zamknięty w górę;
- nie da się wejść spoza
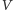 do
do
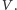
Taki zbiór nazwiemy separatorem. Dodatkowo, zauważmy, że jeśli istnieje
jakikolwiek separator, to nie da się dojść z
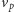 do
do
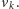 Tu
właściwie wystarczą tylko pierwszy i trzeci warunek, drugi przyda się jedynie
do szukania separatora. Podsumowując, separator istnieje wtedy i tylko wtedy,
gdy nie ma ścieżki z
Tu
właściwie wystarczą tylko pierwszy i trzeci warunek, drugi przyda się jedynie
do szukania separatora. Podsumowując, separator istnieje wtedy i tylko wtedy,
gdy nie ma ścieżki z
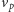 do
do
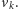 Procedura negatywna będzie
zatem szukała separatora.
Procedura negatywna będzie
zatem szukała separatora.
Jak to zrealizować? Nie można przecież przeszukiwać wszystkich zbiorów wektorów. Po pierwsze, taki zbiór może być nieskończony (czyli nie damy rady zapamiętać wszystkich elementów). Poza tym nie da się wszystkich zbiorów ustawić w ciąg i posprawdzać po kolei (jest ich nieprzeliczalnie wiele) i właściwie nie wiadomo, jak testować warunek drugi i trzeci. Musimy koniecznie znaleźć przynajmniej jakiś sposób zapamiętania takiego zbioru w skończonej pamięci. Teraz właśnie przychodzi nam z pomocą lemat Dicksona.

Rozważmy zbiór minimalnych wektorów danego separatora – wektor
minimalny to taki, że separator nie zawiera elementów mniejszych od niego
w porządku
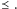 Dzięki lematowi Dicksona wiemy, że jest ich skończenie
wiele. Przypuśćmy bowiem, że mamy nieskończenie wiele wektorów
minimalnych. Ustawiamy je w ciąg
Dzięki lematowi Dicksona wiemy, że jest ich skończenie
wiele. Przypuśćmy bowiem, że mamy nieskończenie wiele wektorów
minimalnych. Ustawiamy je w ciąg
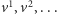 i z lematu Dicksona
dostajemy, że
i z lematu Dicksona
dostajemy, że
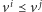 dla pewnych indeksów
dla pewnych indeksów
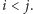 Mamy
sprzeczność z minimalnością
Mamy
sprzeczność z minimalnością
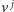 ! Zatem każdy separator składa się ze
skończenie wielu elementów minimalnych
! Zatem każdy separator składa się ze
skończenie wielu elementów minimalnych
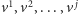 oraz wszystkich
wektorów większych od któregoś z nich. Możemy go zatem reprezentować
poprzez zbiór
oraz wszystkich
wektorów większych od któregoś z nich. Możemy go zatem reprezentować
poprzez zbiór
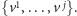
Procedura negatywna przeszukuje więc wszystkie skończone zbiory wektorów
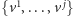 i sprawdza, czy zbiór wszystkich wektorów większych od
któregoś z nich nie jest separatorem. Z podanych powyżej trzech
warunków drugi jest spełniony zawsze. Pierwszy sprawdza się łatwo,
wystarczy porównać współrzędne wektorów
i sprawdza, czy zbiór wszystkich wektorów większych od
któregoś z nich nie jest separatorem. Z podanych powyżej trzech
warunków drugi jest spełniony zawsze. Pierwszy sprawdza się łatwo,
wystarczy porównać współrzędne wektorów
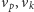 i wektorów
reprezentujących separator. Trzeci również można rozstrzygać w miarę
nietrudno – Czytelnik Ambitny może śmiało spróbować to udowodnić.
i wektorów
reprezentujących separator. Trzeci również można rozstrzygać w miarę
nietrudno – Czytelnik Ambitny może śmiało spróbować to udowodnić.
Tym samym zakończyliśmy opis obu procedur, a więc i algorytmu. Najistotniejszym spostrzeżeniem było, że elementów minimalnych w separatorze jest skończenie wiele. To typowa sytuacja: kluczem do zaprojektowania algorytmu, który zawsze się zatrzymuje, ale, być może, działa bardzo wolno, jest obserwacja, że pewien obiekt pojawiający się w analizie problemu jest skończony. Do otrzymywania takich wyników nadaje się znakomicie lemat Dicksona lub następujący lemat Higmana, stosowany w przypadku słów, a nie wektorów.
Lemat 2 (Higmana). Niech
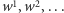 będzie nieskończonym
ciągiem słów nad skończonym alfabetem. Wówczas istnieją takie indeksy
będzie nieskończonym
ciągiem słów nad skończonym alfabetem. Wówczas istnieją takie indeksy
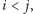 że słowo
że słowo
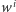 zawiera się w słowie
zawiera się w słowie
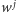 (czyli ciąg
liter słowa
(czyli ciąg
liter słowa
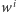 jest podciągiem ciągu liter słowa
jest podciągiem ciągu liter słowa
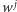 ).
).
Na pierwszy rzut oka widać podobieństwo do lematu Dicksona. Tak naprawdę oba te lematy są szczególnymi przypadkami pewnych bardziej ogólnych twierdzeń. To już jednak temat na zupełnie inną opowieść.